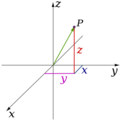Tridimensional para niños
Un objeto es tridimensional si tiene tres dimensiones. Esto significa que podemos ubicar cada uno de sus puntos usando tres medidas. Piensa en el ancho, la altura y la profundidad.
El espacio que nos rodea parece tridimensional. Sin embargo, algunas teorías científicas sugieren que podría haber más dimensiones de las que vemos. Por ejemplo, si incluimos el tiempo como una cuarta dimensión, el universo puede ser visto como un espacio de cuatro dimensiones.
En matemáticas, podemos usar tres números para describir la posición de un punto en un espacio tridimensional. Este espacio se llama espacio euclidiano tridimensional. Es el modelo que usamos para entender el universo físico y la materia que conocemos.
Contenido
Historia de la Geometría Tridimensional
Orígenes en la Antigüedad
Los antiguos griegos ya estudiaban la geometría tridimensional. En los libros XI a XIII de los Elementos de Euclides, se habla de cómo se relacionan las líneas y los planos en el espacio. También se definen figuras sólidas como paralelepípedos, pirámides, prismas, esferas y los sólidos platónicos.
La Geometría Analítica
En el siglo XVII, el matemático René Descartes y Pierre de Fermat desarrollaron la geometría analítica. Esta nueva forma de ver la geometría permitía describir los puntos en el espacio usando coordenadas cartesianas (números). Esto fue un gran avance para entender las formas tridimensionales.
Avances en el Siglo XIX
Durante el siglo XIX, William Rowan Hamilton introdujo los cuaterniones, que ayudaron a describir el espacio tridimensional de una manera más avanzada. Él también inventó los términos escalar y vector, que son muy importantes en la física y las matemáticas. Más tarde, Josiah Willard Gibbs simplificó estas ideas y creó la notación moderna para el producto escalar y el producto vectorial.
El Espacio Físico Tridimensional
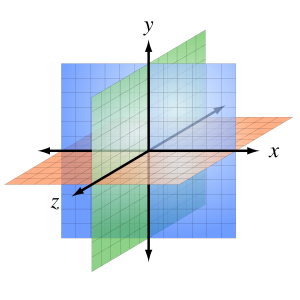
En nuestro día a día, vemos el espacio como tridimensional. Un objeto físico tiene ancho, largo y profundidad o altura. Sin embargo, cuando consideramos fenómenos como la gravedad, la teoría de la relatividad sugiere que el universo es un espacio de cuatro dimensiones, incluyendo el tiempo.
Algunos científicos han pensado por qué tenemos exactamente tres dimensiones espaciales. Por ejemplo, Paul Ehrenfest notó que en universos con más de tres dimensiones, las órbitas planetarias no serían estables. Esto significa que la vida, tal como la conocemos, podría no existir.
Además, algunas teorías físicas modernas, como las teoría de cuerdas, proponen que existen dimensiones adicionales. Estas dimensiones serían muy pequeñas y "enrolladas", por lo que solo se podrían observar en experimentos con partículas muy energéticas.
Geometría Euclidiana Tridimensional
Sistemas de Coordenadas
En matemáticas, para describir un punto en el espacio tridimensional, usamos sistemas de coordenadas. El más común es el sistema de coordenadas cartesianas. Aquí, cada punto se describe con tres números (x, y, z). Estos números indican la distancia del punto desde el origen (el punto donde se cruzan los ejes) a lo largo de tres ejes que son perpendiculares entre sí.
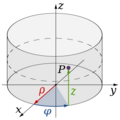
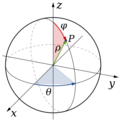
También existen otros sistemas, como las coordenadas cilíndricas y las coordenadas esféricas. Cada uno es útil para diferentes tipos de problemas.
Líneas y Planos
- Dos puntos diferentes siempre forman una línea recta.
- Tres puntos diferentes pueden estar en la misma línea (ser colineales) o formar un único plano.
- Dos líneas distintas pueden cruzarse, ser paralelas o no cruzarse ni estar en el mismo plano (llamadas rectas que se cruzan).
- Dos planos distintos pueden cruzarse en una línea o ser paralelos.
- Una línea puede estar dentro de un plano, cruzarlo en un punto o ser paralela a él.
Esferas y Bolas
Una esfera es el conjunto de todos los puntos en el espacio tridimensional que están a una distancia fija de un punto central. Esta distancia se llama radio. El espacio sólido que está dentro de una esfera se llama bola.
El volumen de una bola se calcula con la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle V = \frac{4}{3}\pi r^{3}} Y la superficie de la esfera se calcula con: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): {\displaystyle A = 4\pi r^2}
Superficies de Revolución
Una superficie de revolución se crea al girar una curva plana alrededor de una línea fija (llamada eje).
- Si la curva es una línea recta que cruza el eje, la superficie es un cono.
- Si la curva es una línea recta paralela al eje, la superficie es un cilindro.
Politopos Regulares
En tres dimensiones, existen nueve formas regulares llamadas politopos. Los más conocidos son los cinco sólidos platónicos convexos.
| Clase | Sólidos platónicos | ||||
|---|---|---|---|---|---|
| Simetría | Td | Oh | Ih | ||
| Grupo de Coxeter | A3, [3,3] | B3, [4,3] | H3, [5,3] | ||
| Orden | 24 | 48 | 120 | ||
| Poliedro regular |
{3,3} |
 {4,3} |
 {3,4} |
 {5,3} |
{3,5} |
Ejemplos de Formas Tridimensionales
Algunas figuras geométricas tridimensionales son:
- Poliedros (con caras planas):
- Superficies curvas:
Estas formas pueden dibujarse o imaginarse en un espacio de tres dimensiones. A veces, cuando hablamos de esferas o cilindros, nos referimos tanto a la superficie como a su interior.
Sistemas Tridimensionales en Ciencias Naturales
En química, se dice que un sistema es tridimensional cuando los enlaces químicos son igual de fuertes en todas las direcciones del espacio. Un ejemplo es el diamante, donde los átomos están unidos en una estructura tridimensional muy fuerte.
En magnetismo, el ordenamiento magnético (cómo se alinean los pequeños imanes dentro de un material) solo es posible si el acoplamiento magnético se extiende en las tres direcciones del espacio.
Simulación 3D
Hoy en día, podemos ver y crear entornos tridimensionales en pantallas bidimensionales, como monitores o televisores. Esto se logra mediante cálculos complejos que proyectan las formas 3D en 2D.
Las computadoras y videoconsolas modernas tienen tarjetas gráficas especiales. Estas tarjetas tienen procesadores llamados GPU (Unidad de Procesamiento Gráfico). Las GPU están diseñadas para hacer rápidamente los cálculos necesarios para mostrar imágenes tridimensionales. Esto ayuda a que la CPU (el cerebro de la computadora) no se sobrecargue y los juegos o programas 3D funcionen de forma fluida.
Véase también
 En inglés: 3D Facts for Kids
En inglés: 3D Facts for Kids
- Bidimensional
- Coordenadas cartesianas
- Gráficos 3D por computadora
- Holografía
- Infografía
- Perspectiva
- Volumen
- Estereoscopía
- Gafas virtuales
- Cuarta dimensión
- Nintendo 3DS