Estadística para niños
La estadística es una disciplina que nos ayuda a entender la variedad de cosas que ocurren a nuestro alrededor. Imagina que quieres saber cuántos de tus compañeros de clase prefieren el fútbol o el baloncesto. La estadística te da las herramientas para recolectar esa información, organizarla, analizarla y presentarla de forma clara.
Contenido
- Estadística: Entendiendo los Datos
- Un Viaje por la Historia de la Estadística
- ¿Cómo se Usa la Estadística Hoy?
- La Estadística en Diferentes Campos
- La Estadística y las Computadoras
- ¿Por Qué es Importante Usar Bien la Estadística?
- La Estadística en la Educación
- La Estadística y el Derecho
- Véase también
Estadística: Entendiendo los Datos
¿Qué es la Estadística?
La estadística es una ciencia formal que siempre está creciendo. Nos ayuda a obtener nuevos conocimientos a través de la observación y la experimentación. Cuando aplicamos la estadística, podemos analizar datos de un grupo pequeño (llamado muestra) para entender mejor un fenómeno más grande. Esto nos permite ver cómo se relacionan las cosas y por qué suceden.
La estadística es muy útil en muchas áreas, desde la física hasta las ciencias sociales, y desde la salud hasta el control de calidad en las fábricas. También se usa en negocios y en el gobierno para describir información y tomar decisiones importantes.
Hoy en día, la estadística nos permite estudiar un grupo de personas o cosas (una población) al:
- Recopilar información.
- Analizar los datos.
- Interpretar los resultados.
Es una herramienta clave para entender fenómenos que ocurren en grandes grupos.
Ramas Principales de la Estadística
La estadística se divide en dos grandes áreas:
Estadística Descriptiva: Organizando la Información
La Estadística descriptiva se encarga de describir, mostrar y resumir los datos que recogemos. Podemos resumir los datos con números o con gráficos. Su objetivo es organizar y describir las características de un conjunto de datos para que sea más fácil entenderlos. Para esto, usamos gráficas, tablas o números.
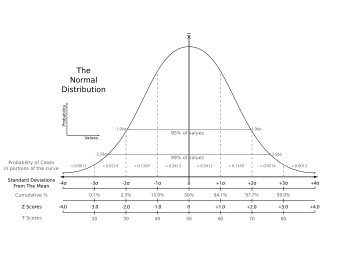
- Ejemplos de números que usamos son la media (el promedio) y la desviación estándar (qué tan dispersos están los datos).
- Ejemplos de gráficos son los histogramas, las pirámides de población y los gráficos circulares.
Estadística Inferencial: Sacando Conclusiones
La Estadística inferencial se usa para crear modelos, hacer predicciones y sacar conclusiones sobre los fenómenos que estudiamos. Tiene en cuenta que las observaciones pueden ser aleatorias. Nos ayuda a encontrar patrones en los datos y a hacer deducciones sobre toda la población que estamos estudiando.
- Por ejemplo, podemos responder preguntas de sí/no (prueba de hipótesis), estimar características numéricas (estimaciones) o predecir lo que podría pasar en el futuro.
- También nos ayuda a ver si hay una correlación (una relación) entre diferentes variables.
Ambas ramas, la descriptiva y la inferencial, se usan en la estadística aplicada. La estadística inferencial se divide a su vez en estadística paramétrica y estadística no paramétrica.
Existe también la estadística matemática, que es la base teórica de todas las técnicas estadísticas. La palabra "estadísticas" (en plural) se refiere a los resúmenes de resultados, como las estadísticas de un partido de fútbol o las estadísticas de ventas.
Un Viaje por la Historia de la Estadística
Los Primeros Pasos de la Estadística
El término Statistik viene del alemán y fue usado por primera vez por Godofredo Achenwall en 1749. Se refería al análisis de datos del Estado, como la "ciencia del Estado". En el siglo XIX, el término "estadística" empezó a significar la recolección y clasificación de datos. Este cambio lo introdujo el escocés sir John Sinclair.
Al principio, la estadística se usaba principalmente en los Estados o ciudades para ayudar a los gobiernos a administrar. Por ejemplo, los censos (conteos de población) empezaron a dar información regular sobre la gente de cada país. Por eso, los datos estadísticos se referían originalmente a la información de la población de una ciudad o Estado.
La Estadística en Civilizaciones Antiguas
Desde hace mucho tiempo, las personas han usado representaciones gráficas en pieles, rocas o paredes de cuevas para contar personas, animales o productos.
- Hacia el año 3000 a.C., los babilonios usaban pequeños recipientes de arcilla para registrar datos sobre la agricultura y el comercio.
- Los egipcios analizaban datos de población y riqueza mucho antes de construir las pirámides.
- Los libros bíblicos de Números y Crónicas incluyen conteos de población y descripciones de la riqueza.
- En China, había registros numéricos similares antes del año 2000 a.C.
- Los antiguos griegos hacían censos para cobrar impuestos.
En la Edad Antigua, los censos se hacían para organizar los impuestos, saber cuántas personas podían servir en el ejército o repartir tierras.
- En Babilonia, se encontraron tablillas de arcilla con registros de negocios.
- En Egipto, desde el año 3050 a.C., los faraones ordenaban censos para planificar la construcción de las pirámides y administrar el Estado. Se registraban cosechas, ganado e impuestos.
- En China, en el año 2238 a.C., el emperador Yao hizo un censo general de la actividad agrícola, industrial y comercial.
- El censo en el pueblo judío se usaba para fines militares y para calcular los ingresos del templo.
- En la Antigua Grecia, los censos servían para saber la distribución de tierras y riquezas, organizar el servicio militar y determinar el derecho al voto.
- En la Antigua Roma, se registraban nacimientos y fallecimientos, y se hacían estudios sobre los ciudadanos y sus bienes.
- En México, en el año 1116, el rey Xólotl ordenó un censo de la población.
La Estadística en la Edad Media y Moderna
Durante la Edad Media, no hubo grandes avances en estadística, pero destaca el trabajo de Isidoro de Sevilla, quien recopiló y clasificó datos en su obra Originum sive Etymologiarum.
En la Edad Moderna:
- En España, se hicieron censos importantes como el de Pecheros (1528) y el del conde de Aranda (1768).
- En Inglaterra, una enfermedad en el siglo XVI hizo que se llevaran muchos registros de fallecimientos y nacimientos.
El Nacimiento de la Probabilidad en Estadística
Los métodos estadístico-matemáticos surgieron de la teoría de probabilidad, que comenzó con la correspondencia entre Pascal y Pierre de Fermat en 1654. Christian Huygens (1657) hizo el primer estudio científico conocido sobre el tema. Más tarde, Jakob Bernoulli y Abraham de Moivre estudiaron la probabilidad como una rama de las matemáticas.
La teoría de errores (cómo medir y corregir errores en las observaciones) se desarrolló con trabajos de Roger Cotes y Thomas Simpson en el siglo XVIII. Pierre-Simon Laplace intentó deducir reglas para combinar observaciones usando la teoría de probabilidades.

El método de mínimos cuadrados, que se usa para reducir errores en las mediciones, fue publicado por Adrien-Marie Legendre y Carl Friedrich Gauss. Gauss lo usó para predecir la ubicación del planeta enano Ceres en 1801. Otros científicos como Daniel Bernoulli también hicieron contribuciones importantes.
Adolphe Quetelet (1796-1874) fue otro fundador importante de la estadística. Él introdujo la idea del "hombre promedio" para entender fenómenos sociales complejos.
La Estadística en los Siglos XX y XXI

La estadística moderna surgió a principios del siglo XX gracias al trabajo de Francis Galton y Karl Pearson. Ellos hicieron de la estadística una disciplina matemática rigurosa. Galton aportó conceptos como la desviación típica, la correlación y el análisis de la regresión. Pearson desarrolló el coeficiente de correlación de Pearson y fundó la revista Biometrika y el primer departamento de estadística en la University College de Londres.
En el siglo XX, la necesidad de herramientas precisas para la salud pública y la economía impulsó grandes avances en la estadística.
Ronald Fisher fue otra figura clave, con libros que definieron la disciplina académica. Él introdujo el término varianza y desarrolló modelos para el diseño experimental.
Hoy en día, la estadística se usa mucho más allá de los gobiernos. Personas y organizaciones la utilizan para entender datos y tomar decisiones en ciencias naturales, ciencias sociales, medicina, negocios y otras áreas. Es una parte fundamental de las matemáticas aplicadas y ayuda al avance del conocimiento científico. Muchas universidades tienen departamentos de estadística o la enseñan en otras áreas como psicología o educación.
¿Cómo se Usa la Estadística Hoy?
Cuando aplicamos la estadística a un problema, empezamos por identificar el grupo o proceso que queremos estudiar. Puede ser la población de un país, los granos de una roca o los productos de una fábrica.
Para ser prácticos, en lugar de estudiar a toda la población, usualmente estudiamos una parte más pequeña, llamada muestra. Recogemos datos de esta muestra, ya sea observando o haciendo experimentos. Luego, analizamos los datos para describirlos y sacar conclusiones.
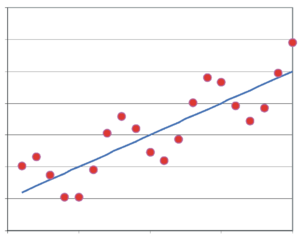
El concepto de correlación es muy importante. Un análisis estadístico puede mostrar que dos variables (dos características de lo que estudiamos) tienden a cambiar juntas. Por ejemplo, un estudio podría mostrar que las personas con menos ingresos tienden a vivir menos años. Esto significa que las dos variables están correlacionadas. Sin embargo, esto no siempre significa que una cause la otra. Podría haber una tercera variable que esté influyendo.
Si la muestra es una buena representación de la población, las conclusiones que sacamos de la muestra pueden aplicarse a toda la población. La estadística nos ayuda a saber qué tan representativa es una muestra y a corregir posibles errores.
El concepto matemático principal para entender la aleatoriedad es la probabilidad. La estadística matemática usa la teoría de probabilidades y el análisis matemático para entender las bases de la estadística.
Es muy importante usar los métodos estadísticos correctamente. Si se usan mal, pueden llevar a errores graves en la descripción y la interpretación de los datos. Esto podría afectar decisiones importantes en la sociedad o en la ciencia.
A veces, los resultados estadísticos pueden ser difíciles de entender para alguien que no es experto. Por eso, es importante tener una "cultura estadística" básica para manejar la información en el día a día.
Población y Muestra: ¿A Quién Estudiamos?
- Población: Es el grupo completo de todo lo que nos interesa estudiar. Pueden ser personas, medidas u objetos. Por ejemplo, todos los estudiantes de una escuela. Cuando analizamos a toda la población, se llama censo.
- Población finita: Es un grupo que podemos contar por completo. Tiene un número limitado de elementos. Por ejemplo, el número de alumnos en tu clase.
- Población infinita: Es un grupo tan grande que no podemos contarlo por completo. Tiene un número ilimitado de elementos. Por ejemplo, todos los posibles resultados al lanzar un dado muchas veces.
- Muestra: Es una parte más pequeña de la población. Se forma con algunos datos de ese grupo grande. Estudiar una muestra se llama muestreo.
- Muestra representativa: Es una parte de la población que tiene las mismas características importantes que el grupo completo. Para que sea representativa, se deben seguir ciertos pasos al seleccionarla. Así, podemos sacar conclusiones sobre toda la población sin tener que examinar cada uno de sus elementos.
Parámetros: Las Medidas Clave
- Parámetro: Es una medida que describe una característica numérica de una población. Se suele representar con símbolos griegos (como μ o σ).
Estudios Experimentales y Observacionales
Un objetivo común en la investigación es entender las causas y efectos. Queremos saber cómo los cambios en algunas variables (llamadas variables independientes) afectan a otras variables (llamadas variables dependientes). Hay dos tipos principales de estudios para esto:
- Estudios experimentales: El investigador controla y manipula las variables independientes para ver su efecto.
- Estudios observacionales: El investigador solo observa las variables sin manipularlas.
Ambos tipos pueden ser muy efectivos, y la estadística es fundamental para analizar la información que se obtiene.
Niveles de Medición: ¿Cómo Medimos?
En estadística, hay cuatro formas de medir o escalas de medición:
- Nominal: Agrupa objetos en clases sin ningún orden. Por ejemplo, tipos de frutas (manzana, plátano, naranja).
- Ordinal: Ordena los valores, pero las diferencias entre ellos no son exactas. Por ejemplo, el nivel de satisfacción (bajo, medio, alto).
- Intervalo: Tiene una unidad de medida constante y las distancias entre valores son significativas, pero el cero es arbitrario (no significa ausencia total). Por ejemplo, la temperatura en grados Celsius.
- Razón: Es el nivel más completo. Tiene una unidad de medida constante y un cero real que significa ausencia total. Por ejemplo, la altura o el peso.
Cuanto más alto es el nivel de medición, más flexibles son los métodos estadísticos que podemos usar para analizar los datos.
La Estadística en Diferentes Campos
Muchos campos de investigación usan la estadística de forma muy extensa y tienen su propia terminología. Algunas de estas disciplinas incluyen:
La estadística es esencial para los negocios y la producción. Se usa para entender cómo varían los sistemas de medición, para el control estadístico de procesos y para tomar decisiones cuando hay incertidumbre.
La Estadística y las Computadoras
El rápido avance de las computadoras desde la segunda mitad del siglo XX ha cambiado mucho la estadística. Antes, la mayoría de los modelos estadísticos eran simples. Ahora, las computadoras y los algoritmos avanzados han permitido el uso de modelos más complejos, como las redes neuronales y los árboles de decisión.
El aumento del poder de cálculo también ha hecho populares métodos que requieren mucha computación, como los tests de permutación y de bootstrap. Esto ha llevado a un nuevo enfoque en la estadística "experimental" y "empírica". Hoy en día, hay muchos paquetes estadísticos (programas de computadora) disponibles para los investigadores.
¿Por Qué es Importante Usar Bien la Estadística?
A veces, se piensa que la estadística se usa de forma incorrecta para presentar los datos de una manera que favorezca a quien los muestra. Hay una frase famosa que dice: "Hay tres tipos de mentiras: mentiras pequeñas, mentiras grandes y estadísticas". El libro How to lie with statistics (Cómo mentir con las estadísticas) de Darrell Huff explica muchos casos de mal uso de la estadística, especialmente con gráficos que se pueden malinterpretar.
Si se elige o se modifica una muestra de datos sin seguir reglas claras, los resultados pueden ser engañosos. Esto puede pasar por errores no intencionados o por falta de conocimiento estadístico. Por eso, es muy importante que el análisis estadístico lo hagan profesionales capacitados.
Cuando personas sin la preparación adecuada usan la estadística, uno de los errores más comunes es no entender el error de tipo I, lo que puede llevar a conclusiones falsas. La probabilidad de encontrar una relación falsa entre dos variables aumenta si se "juega" con los datos sin una hipótesis clara. Esta mala práctica, llamada p-hacking, consiste en buscar relaciones significativas sin una razón previa. Esto puede hacer que algunos estudios se contradigan entre sí y que la gente desconfíe de la ciencia. Por ejemplo, un día se dice que un alimento es bueno y al día siguiente, otro estudio dice lo contrario. Esto puede pasar porque se usan métodos diferentes, técnicas incorrectas o muestras muy pequeñas.
La Estadística en la Educación
El análisis de datos estadísticos se usa mucho en la educación. Por ejemplo, las estadísticas de visitas a los artículos de Wikipedia pueden ayudar a saber qué temas son más estudiados en los diferentes países. En la Wikipedia en alemán, algunos temas educativos tienen una sección llamada "Didaktic" con sugerencias para estudiantes y profesores.
Podemos ver el número de visitas de un artículo de Wikipedia a lo largo del tiempo. Por ejemplo, en el artículo de "estadística", se puede notar que hay menos consultas los fines de semana y un gran aumento a mitad de semana. Esto puede deberse a que los estudiantes lo consultan para sus tareas o exámenes.
La enseñanza de la estadística debe enfocarse en cómo elegir las pruebas correctas, interpretar los resultados y usar programas de computadora. Este enfoque práctico ayuda a los estudiantes a sentirse más seguros al aplicar la estadística.
La Estadística y el Derecho
La abogacía, como muchas otras profesiones, se relaciona con la estadística. La estadística proporciona datos necesarios para entender qué aspectos de la sociedad necesitan ser regulados. Su función principal es asegurar la fiabilidad y validez de la información.
Según Torres Manrique, el "Derecho Estadístico" es una disciplina jurídica que estudia de forma numérica y cualitativa las tendencias y frecuencias de fenómenos masivos. Su objetivo es ayudar a que la vida en sociedad sea más justa y menos manipulable.
La estadística es una herramienta de apoyo para la administración de justicia. Sin embargo, es importante tener cuidado, ya que los datos pueden usarse de forma incorrecta. En los juicios, la estadística puede influir en la decisión sobre la inocencia o culpabilidad de una persona. Lamentablemente, en muchos países de Latinoamérica, los enfoques estadísticos rigurosos en el derecho son mínimos.
Para que los juicios sean más precisos, se deberían realizar estudios como la Criminología Estadística. Esta disciplina ayuda a los profesionales del derecho con principios y técnicas importantes para sus investigaciones.
Véase también
 En inglés: Statistics Facts for Kids
En inglés: Statistics Facts for Kids
- Computación científica
- Día Mundial de la Estadística
- Método Delphi
- Teoría de probabilidad
- Organización estadística de España
- Anuario Estadístico de España
- Medidas de tendencia central
- Sabermetría
- Debabrata Basu
- Teoría del aprendizaje estadístico
- Censos de población por país a nivel mundial