Regresión lineal para niños
En estadística, la regresión lineal o ajuste lineal es una herramienta matemática que nos ayuda a entender y predecir cómo se relacionan diferentes cosas. Imagina que tienes un grupo de puntos en un gráfico y quieres encontrar la línea recta que mejor los represente. Esa línea es lo que la regresión lineal busca.
Este método se usa para ver cómo una variable dependiente (algo que queremos entender o predecir, como la altura de una planta) se ve afectada por una o más variables independientes (cosas que podrían influir, como la cantidad de agua que recibe la planta). Si no se puede encontrar una relación clara, decimos que no hay correlación.
La idea es encontrar una fórmula sencilla que describa esta relación, algo así como: Y = un número + (otro número * X) + un pequeño error
Donde:
- Y es la variable que queremos predecir (por ejemplo, la altura de la planta).
- X es la variable que creemos que influye (por ejemplo, la cantidad de agua).
- Los "números" son los que nos dicen cuánto influye X en Y.
- El "pequeño error" es la parte que no podemos explicar con nuestras variables.
La regresión lineal es diferente de la regresión no lineal, que usa curvas en lugar de líneas rectas.
Contenido
¿Cómo surgió la Regresión Lineal?
La primera vez que se documentó una idea parecida a la regresión lineal fue en 1805, con el método de los mínimos cuadrados, publicado por Legendre. Más tarde, Gauss lo desarrolló aún más.
La palabra "regresión" se usó por primera vez en un estudio sobre la estatura de las personas. Se notó que los hijos de padres muy altos o muy bajos tendían a tener una estatura más cercana al promedio general. Es decir, "regresaban" hacia la media.
El término "lineal" se usa para diferenciar este método de otros que usan funciones más complejas. Los modelos lineales son más sencillos de entender y tienen una base matemática muy sólida.
El Modelo de Regresión Lineal: ¿Cómo funciona?
El modelo de regresión lineal se usa cuando la variable que influye (X) puede tomar cualquier valor continuo (como la temperatura o el tiempo). Este modelo conecta la variable que queremos predecir (Y) con las variables que influyen (X), buscando una línea recta que las relacione.
La fórmula general es: Y = β0 + β1X1 + ... + βmXm + ε
Aquí, "ε" (épsilon) representa un factor aleatorio, como el azar o cosas que no podemos medir. Es lo que hace que el modelo sea un poco impredecible.
En el caso más simple, con una sola variable que influye, la fórmula es como la de una línea recta: Y = β0 + β1X1 + ε
El objetivo de la regresión es encontrar los mejores valores para los números (β0, β1, etc.) para que la línea se ajuste lo mejor posible a los datos que tenemos. Para ello, se usan datos de observaciones reales.
Una vez que tenemos la línea de regresión, es importante ver qué tan bien se ajusta a los datos. Esto se hace con un análisis especial que nos dice si el modelo es adecuado o no.
¿Qué se necesita para que el modelo funcione bien?
Para que un modelo de regresión lineal funcione correctamente, se deben cumplir algunas condiciones importantes:
- Error promedio cero: Los errores (la diferencia entre la línea y los puntos reales) deben ser aleatorios, sin un patrón. Algunos serán positivos y otros negativos, pero su promedio debe ser cero.
- Varianza constante: La dispersión de los errores debe ser la misma en todos los puntos.
- Errores independientes: El error de un punto no debe influir en el error de otro punto.
- Variables que influyen sin relación exacta: Las variables que usamos para predecir no deben estar perfectamente relacionadas entre sí.
- Suficientes datos: Necesitamos tener más datos que variables para que el modelo sea útil.
- Errores normales: Los errores deben seguir una distribución normal (como una campana).
Tipos de Modelos de Regresión Lineal
Existen diferentes tipos de regresión lineal, dependiendo de cuántas variables usemos para predecir.
Regresión Lineal Simple
Este es el tipo más básico. Solo usa dos variables: una variable independiente (X) y una variable dependiente (Y). Se asume que la relación entre ellas es una línea recta.
La fórmula es: Y = β0 + β1X + ε
- β1 (beta uno) es la pendiente de la línea. Nos dice cuánto cambia Y por cada unidad que cambia X.
- β0 (beta cero) es el punto donde la línea cruza el eje Y.
Para encontrar los mejores valores de β0 y β1, se usa el método de los mínimos cuadrados. Este método busca la línea que minimiza la suma de las distancias al cuadrado entre los puntos reales y la línea.
A veces, una línea recta no es la mejor opción. En esos casos, se pueden usar modelos que transforman la línea en otro tipo de curva, como una función exponencial.
Regresión Lineal Múltiple
La regresión lineal múltiple se usa cuando queremos analizar la relación entre una variable dependiente (Y) y varias variables independientes (X1, X2, etc.). Es muy útil cuando muchas cosas pueden influir en lo que queremos predecir.
La fórmula es: Y = β0 + β1X1 + β2X2 + ... + βmXm + ε
Aquí, cada β (beta) nos dice cuánto influye cada variable X en Y.
Para encontrar los mejores valores de estos β, también se usa el método de los mínimos cuadrados, pero los cálculos son más complejos y a menudo se hacen con computadoras.
Al igual que en la regresión simple, es crucial verificar qué tan bien se ajusta el modelo a los datos usando un análisis especial.
Rectas de Regresión
Las rectas de regresión son las líneas que mejor se ajustan a un grupo de puntos en un gráfico (llamado diagrama de dispersión).
Hay dos posibles rectas de ajuste máximo:
- La recta que predice Y a partir de X.
- La recta que predice X a partir de Y.
La "correlación" (un valor entre 0 y 1) nos dice qué tan bueno es el ajuste. Si la correlación es cercana a 1, el ajuste es muy bueno y las predicciones serán confiables. Si es cercana a 0, el ajuste es malo y las predicciones no serán fiables.
Ambas rectas se cruzan en un punto especial llamado centro de gravedad de la distribución de los datos.
Aplicaciones de la Regresión Lineal
La regresión lineal se usa en muchísimos campos, desde la ciencia hasta la industria, porque muchas situaciones de la vida real muestran comportamientos que se pueden representar con líneas rectas.
Líneas de Tendencia
Las líneas de tendencia muestran cómo cambian los datos a lo largo del tiempo. Por ejemplo, pueden indicar si el precio del petróleo o el valor de las acciones han subido o bajado. Aunque se pueden dibujar a ojo, la regresión lineal las calcula de forma muy precisa.
Medicina
En medicina, la regresión lineal se usó en los primeros estudios que relacionaron el riesgo de enfermedades con el hábito de fumar. Los investigadores incluyen muchas variables para asegurarse de que los resultados no se deban a otras causas, como la situación económica de las personas.
Química
En la industria química, es importante saber la concentración de un elemento. Se usa un aparato llamado espectrofotómetro, que necesita ser calibrado. Para esto, se crea una "recta de calibración" usando la regresión lineal, que relaciona la luz que absorbe una sustancia con su concentración.
Mecánica
En mecánica, la regresión lineal ayuda a estudiar cómo los materiales se desgastan con el uso repetido. Se usa para ajustar una ecuación que relaciona el desgaste con el número de veces que un material es sometido a esfuerzo.
Electricidad
En electricidad, se puede usar la regresión lineal para calcular el valor de una resistencia en un circuito. Se miden pares de datos de voltaje e intensidad y se ajusta una línea para encontrar el valor de la resistencia.
Sensores
Los sensores, como los que miden la temperatura, necesitan ser calibrados. La regresión lineal se usa para encontrar la relación entre la señal que da el sensor y la temperatura real, lo que permite que el sensor sea preciso.
Física
En física, se puede determinar el coeficiente de rozamiento de un objeto. Se mide el ángulo de inclinación de una rampa y se usa la regresión lineal para encontrar la ecuación que describe el rozamiento y el error en la medición.
Fabricación
En la fabricación, especialmente en soldadura, la regresión lineal ayuda a relacionar la intensidad de la corriente y la velocidad de alimentación del hilo con la distancia entre el hilo y la zona a soldar. Esto permite controlar mejor el proceso.
Diseño de Experimentos
Esta técnica ayuda a mejorar procesos industriales. Por ejemplo, se puede usar la regresión lineal para encontrar la relación entre la temperatura y la presión en un proceso, y así optimizarlo.
Construcción
En la construcción, la regresión lineal se usa para entender las propiedades del hormigón. Por ejemplo, puede predecir la resistencia del hormigón a partir de su elasticidad, o cómo absorbe agua con el tiempo.
Informática
La regresión lineal es una herramienta fundamental en la programación y el análisis de datos. Se puede implementar en lenguajes como JavaScript, PHP o Python para predecir valores futuros o analizar tendencias. Por ejemplo, un programa podría usarla para proyectar el progreso de un proyecto.
Ejemplos Prácticos de Regresión Lineal
Aplicación en la Pigmentación de Pinturas para Automóviles
Imagina una empresa que pinta partes de coches. Es muy importante que el color sea exacto. La cantidad de pigmento en la pintura influye en el color final. La regresión lineal puede ayudar a predecir cuánta pigmentación se necesita para obtener el color exacto que piden los fabricantes de coches.
Si la cantidad de pigmento (variable independiente X) se relaciona con la resolución del color (variable dependiente Y), podemos usar una fórmula como: Y = un número + (otro número * X)
Esto ayuda a la empresa a reducir errores, ahorrar tiempo y materiales, y asegurar que el color de la pintura sea siempre el correcto.
Por ejemplo, si se ajusta la cantidad de pigmento blanco y se toman medidas del color, la regresión lineal puede encontrar la mejor línea que relacione el pigmento con el color. Esto permite a la empresa estandarizar sus procesos y tener una idea clara de cómo controlar el color.
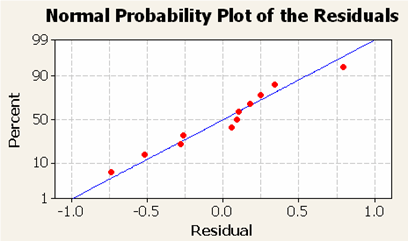Figura 2. Gráfica de probabilidad.
Aplicación en el Análisis Químico
En un laboratorio, el rendimiento de una reacción química puede depender de la temperatura y de la concentración de los ingredientes. La regresión lineal múltiple puede analizar estos datos para encontrar la fórmula que predice el rendimiento.
Por ejemplo, si tenemos datos de rendimiento, concentración y temperatura, la regresión lineal nos puede dar una ecuación como: Rendimiento = un número + (otro número * Concentración) + (otro número * Temperatura)
Esto permite a los químicos entender qué tan importantes son la temperatura y la concentración para el resultado de la reacción. También pueden usar gráficos para asegurarse de que el modelo es válido y que los resultados son confiables.
Galería de imágenes
Véase también
En inglés: Linear regression Facts for Kids
- Homoscedasticidad
- Regresión logística
- Mínimos cuadrados
- Cuarteto de Anscombe
