Econometría para niños
Datos para niños Econometría |
||
|---|---|---|
| Campo de estudio | ||
 |
||
| Visión estadística Econometría frecuentista Econometría bayesiana |
||
| Visión económica Macroeconometría Microeconometría |
||
| Divisiones Econometría Econometría financiera Econometría espacial Econometría estructural Econometría computacional (IA, ML, DL...) Econometría aplicada Causalidad y Econometría |
||
| ' | ||
 |
||
La econometría es una rama de la economía que usa herramientas de las matemáticas y la estadística. Su nombre viene del griego y significa "medida de la casa" o "medida de la economía".
Esta disciplina nos ayuda a entender y predecir cómo funcionan los sistemas económicos. Para ello, analiza datos sobre cosas como los precios de los productos, las tasas de interés, el valor de las monedas o cómo reacciona el mercado. También estudia los costos de producción y las tendencias de los negocios. La econometría es muy útil para ver las consecuencias de las decisiones económicas de un país.
Contenido
¿Qué es la econometría?
La economía es una ciencia social que explica cómo funciona el sistema económico. Esto incluye la producción, el consumo, el dinero y cómo se reparte el ingreso. Los economistas suelen crear modelos económicos teóricos. Estos modelos describen cómo se comportan las personas y las empresas.
Sin embargo, estos modelos necesitan ser probados con datos reales. Así podemos saber si explican bien lo que pasa y si pueden predecir el futuro. La econometría se encarga de construir estos modelos usando datos. También usa técnicas de la ciencia de datos y el aprendizaje automático.
Los expertos en econometría intentan usar métodos similares a los de las ciencias naturales. Sin embargo, estudiar el comportamiento de las personas es muy complejo.
La econometría combina las matemáticas, la estadística, la investigación social y la teoría económica. Uno de los desafíos es la falta de datos o que estos datos puedan tener errores. A pesar de esto, la econometría es la forma más científica de entender los fenómenos económicos. Sus resultados son cada vez más precisos.
¿Cómo definen la econometría los expertos?
Muchos economistas importantes han dado su propia definición de econometría:
- Ragnar Frisch (1930): Dijo que la econometría es la unión de la estadística, la teoría económica y las matemáticas. Esta unión crea una herramienta poderosa para analizar la economía.
- Paul Samuelson, Tjalling Koopmans y Richard Stone (1954): La describieron como el análisis de fenómenos económicos actuales. Se basa en la teoría y las observaciones, usando métodos adecuados.
- Valavanis (1959): Explicó que el objetivo de la econometría es poner las teorías económicas en forma matemática. Así se pueden verificar con estadística y medir el impacto de una variable sobre otra. También sirve para predecir eventos futuros.
- Lawrence Klein (1962): Su objetivo principal es dar un significado real a las ideas económicas.
- Malinvaud (1966): La definió como la aplicación de las matemáticas y la estadística al estudio de los fenómenos económicos.
¿Para qué sirve la econometría?
La econometría toma datos reales de la economía. Luego, usa el análisis estadístico y matemático para encontrar los valores de los modelos. Estos modelos explican cómo se relacionan las variables económicas.
También sirve para:
- Comprobar si los modelos son válidos.
- Ver si los modelos pueden explicar la economía de una empresa o de un país.
- Entender cómo evolucionan las cosas con el tiempo.
- Predecir valores futuros de las variables económicas.
- Sugerir medidas para la política económica. Por ejemplo, para decidir cuánto debe recaudar un gobierno en impuestos.
¿Qué es un modelo econométrico?
Un modelo econométrico busca explicar una variable usando otras. Primero, se parte de un modelo económico. Este se convierte en econométrico cuando se le añaden detalles para poder usarlo con datos reales.
Esto significa que se definen:
- Las variables que explican y determinan el modelo.
- Los números que acompañan a las variables (parámetros).
- Las ecuaciones matemáticas.
- Un "error aleatorio" que explica la parte del modelo que no es sistemática.
- Los datos estadísticos.
Después de definir el modelo, se le asignan valores numéricos a los parámetros. Para esto se usan métodos estadísticos, como los mínimos cuadrados.
La tercera etapa es la verificación. Aquí se comprueba si el modelo es válido usando pruebas estadísticas.
Finalmente, el modelo se aplica para su objetivo. Los modelos econométricos son útiles para:
- Entender cómo funciona la economía.
- Predecir valores futuros de las variables económicas.
- Simular diferentes escenarios para planificar.
- Encontrar los valores óptimos para las decisiones económicas.
Métodos de la econometría
El método de mínimos cuadrados
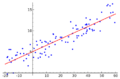
Este método también se conoce como teoría de la regresión lineal. Es una herramienta estadística muy usada en econometría.
Se usa para representar relaciones lineales entre una variable que queremos explicar (variable endógena) y una o más variables que la explican (variables exógenas). Se ve así:
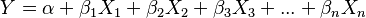
O de esta otra forma:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \alpha + \sum _{{i=1}}^{n} \beta_{i} X_{i} = Y
Aquí, "Y" es la variable que queremos entender. Las variables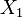 
hasta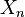 
son las que la determinan. La elección de estas variables depende de la teoría económica. El objetivo es encontrar los valores de 
hasta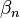 
. A veces se añade una constante, 
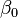, al modelo:
.
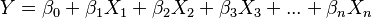O así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \beta_{0} + \sum _{{i=1}}^{n} \beta_{i} X_{i} = Y
Además, se asume que la relación no es perfecta. Siempre habrá un pequeño error aleatorio, representado por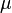 
. Este error incluye todos los factores que no se pudieron incluir en el modelo.
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Y=\beta_{0}+\beta_{1}X_{1}+\beta_{2}X_{2}+\beta_{3}X_{3}+...+\beta_{n}X_{n}+ \mu \
O de esta manera:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \beta_{0} + \left(\sum _{{i=1}}^{n} \beta_{i} X_{i}\right)+\mu = Y
Se suele pensar que 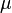es una variable aleatoria normal, con un promedio de cero y una variación constante.
Para usar este método, se toman datos reales. Por ejemplo, se pueden observar los precios y el empleo de un país a lo largo de varios años. O se pueden comparar estos datos en diferentes países en un mismo año. Cada uno de estos conjuntos de datos se llama "observación muestral".
Una vez que se tienen los datos, se aplica el método de mínimos cuadrados. Este método busca los valores de los parámetros que minimizan la suma de los errores al cuadrado. Los errores son la diferencia entre los valores predichos por el modelo y los valores reales. Los parámetros que logran este mínimo son los que se consideran correctos.
Este método también nos da información adicional. Con ella, podemos saber si los valores de los parámetros son confiables. También podemos hacer "contrastes de hipótesis". Esto significa verificar si ciertas suposiciones sobre el modelo son ciertas o no. Además, nos ayuda a ver si se pueden quitar algunas variables o si los valores de los parámetros han cambiado con el tiempo.
Desafíos del método de mínimos cuadrados
El método de mínimos cuadrados tiene algunos desafíos que los investigadores han tratado de resolver:
- Relaciones no lineales: El método asume que las relaciones entre variables son lineales. Si no lo son, se usan otros métodos para transformarlas o aproximarlas.
- Normalidad de los errores: Se asume que los errores del modelo siguen una distribución normal. Esto es importante para muestras pequeñas. Para muestras grandes, el teorema del límite central ayuda a justificar esta suposición.
- Varianza cambiante (Heterocedasticidad): A veces, la variación de los errores del modelo cambia con el tiempo. Esto se llama heterocedasticidad. Se detecta con técnicas estadísticas y se corrige usando métodos como los mínimos cuadrados generalizados.
- Errores correlacionados (Autocorrelación): Si los errores de diferentes períodos están relacionados entre sí, se llama autocorrelación. También hay métodos para detectar y corregir este problema.
- Multicolinealidad: Esto ocurre cuando una variable explicativa depende de otra variable explicativa en el mismo modelo. Esto puede afectar la información y hacer que el método no funcione bien. La solución suele ser identificar qué variables causan el problema y ajustar el modelo.
- Relaciones dinámicas: En algunos modelos, una variable puede depender de sus propios valores pasados o de los valores pasados de otras variables. Para esto, se estudian los modelos de series temporales.
Programas para econometría
Existen muchos programas de computadora que se usan para hacer econometría. Algunos de los más populares son Stata, R, SAS, SPSS, EViews, Gretl y Matlab.
R es un lenguaje de programación muy potente para la econometría. Otros lenguajes como Java, Python o C++ también pueden usarse para análisis econométricos.
Programas como SPSS y Stata, aunque son estadísticos, permiten hacer análisis econométricos muy avanzados. Gretl es conocido por ser fácil de usar y muy eficiente para las series de tiempo. Eviews fue creado específicamente para la econometría.
Incluso algunas calculadoras científicas avanzadas pueden hacer análisis econométricos básicos. Programas matemáticos como MATLAB, Maple y Scilab también pueden realizar estos análisis, aunque pueden tener limitaciones en la cantidad de datos que manejan.
La elección del programa depende de tu sistema operativo (como Windows, GNU Linux o Mac OS) y de lo que quieras lograr. Si necesitas algo muy personalizado para publicaciones profesionales, los lenguajes de programación son ideales. Permiten presentar la información de una forma única.
Galería de imágenes
-
Un ejemplo de regresión lineal, una técnica usada en econometría.
-
Un histograma que muestra una distribución normal, importante para los errores en los modelos econométricos.
Véase también
En inglés: Econometrics Facts for Kids
