Errores de tipo I y de tipo II para niños
En el mundo de la investigación y la estadística, a veces se cometen errores al sacar conclusiones. Estos errores son importantes de entender, especialmente cuando se realizan pruebas para saber si una idea o "hipótesis" es verdadera o falsa.
Imagina que un científico tiene una idea inicial, a la que llamamos hipótesis nula (se escribe 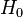 ). Esta hipótesis nula es como el "estado normal" o lo que se cree que es cierto hasta que se demuestre lo contrario. Por ejemplo, si un médico prueba un nuevo medicamento, la hipótesis nula podría ser: "El medicamento no tiene ningún efecto".
). Esta hipótesis nula es como el "estado normal" o lo que se cree que es cierto hasta que se demuestre lo contrario. Por ejemplo, si un médico prueba un nuevo medicamento, la hipótesis nula podría ser: "El medicamento no tiene ningún efecto".
Existen dos tipos principales de errores que pueden ocurrir al probar estas ideas: el error de tipo I y el error de tipo II.
Contenido
¿Qué es el Error de Tipo I o Falso Positivo?
El error de tipo I, también conocido como error de tipo alfa (α) o falso positivo, ocurre cuando un investigador decide que su idea inicial (la hipótesis nula) es falsa, pero en realidad, ¡es verdadera! Es como decir que algo es cierto cuando no lo es.
Piensa en estos ejemplos para entenderlo mejor:
- En medicina: Si un médico dice que un paciente está enfermo, pero en realidad el paciente está sano. Aquí, la hipótesis nula era: "El paciente está sano". El error es decir que no lo está, cuando sí lo está.
- En un juicio: Si se declara que una persona es culpable, pero en realidad es inocente. La hipótesis nula era: "El acusado es inocente". El error es rechazar esa idea cuando era cierta.
- En un control de acceso: Si no se permite la entrada a alguien que sí tiene derecho a entrar. La hipótesis nula era: "La persona tiene derecho a ingresar". El error es decir que no lo tiene, cuando sí lo tiene.
Este tipo de error se relaciona con el nivel de significancia estadística, que es la probabilidad que el investigador está dispuesto a aceptar de cometer este error.
¿Qué es el Error de Tipo II o Falso Negativo?
El error de tipo II, también llamado error de tipo beta (β) o falso negativo, sucede cuando un investigador no rechaza la hipótesis nula, pero en realidad, ¡esa hipótesis nula es falsa! Es decir, se concluye que no hay una diferencia o efecto, cuando en realidad sí lo hay.
Por ejemplo, si un médico dice que un paciente está sano, pero en realidad el paciente sí está enfermo. Aquí, la hipótesis nula era: "El paciente está sano". El error es no rechazar esa idea, cuando en realidad el paciente no está sano.
A diferencia del error de tipo I, la probabilidad de cometer un error de tipo II es más difícil de calcular. Esto se debe a que la hipótesis alternativa (la idea opuesta a la hipótesis nula) puede abarcar muchas posibilidades.
¿Qué es la Potencia de un Estudio?
La potencia de un estudio es la probabilidad de encontrar una diferencia o un efecto en la muestra que se está estudiando, si esa diferencia o efecto realmente existe en la población. Es lo contrario al error de tipo II. Se calcula como 1 menos la probabilidad del error de tipo II (1 − β). Cuanto mayor sea la potencia, mejor será el estudio para detectar lo que busca.
Errores al Probar Hipótesis
Cuando se realiza una contraste de hipótesis (una prueba para decidir si una idea es verdadera o falsa), se elige entre la hipótesis nula (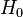 ) y la hipótesis alternativa (
) y la hipótesis alternativa (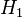 ). La hipótesis alternativa es la idea que se quiere probar, la que dice que hay un efecto o una diferencia.
). La hipótesis alternativa es la idea que se quiere probar, la que dice que hay un efecto o una diferencia.
Pueden ocurrir cuatro situaciones diferentes, como se muestra en esta tabla:
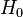 es cierta es cierta |
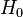 no es cierta no es cierta |
|
|---|---|---|
Se escogió 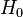 |
No hay error (1 − α o verdadero negativo) | Error de tipo II (β o falso negativo) |
Se escogió 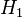 |
Error de tipo I (α o falso positivo) | No hay error (1 − β o verdadero positivo) |
La probabilidad de cometer un error de tipo I se representa con la letra griega α (alfa). La probabilidad de cometer un error de tipo II se representa con la letra griega β (beta).
La potencia del contraste es la probabilidad de elegir la hipótesis alternativa (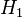 ) cuando esta es realmente cierta. Se calcula como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1-\beta\, .
) cuando esta es realmente cierta. Se calcula como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1-\beta\, .
Cuando se diseña un estudio, se busca que las probabilidades de ambos tipos de error sean lo más pequeñas posible. Sin embargo, si el tamaño de la muestra (la cantidad de personas o cosas que se estudian) es fijo, al disminuir la probabilidad del error de tipo I (α), la probabilidad del error de tipo II (β) tiende a aumentar.
Normalmente, los estudios se diseñan para que la probabilidad de error de tipo I (α) sea del 5% (0.05). A veces se usan valores del 10% (0.1) o 1% (0.01), dependiendo de lo estrictas que deban ser las condiciones. Para aumentar la potencia de un estudio (es decir, disminuir el error de tipo II), se puede aumentar el tamaño de la muestra. Sin embargo, esto a menudo significa que el estudio será más costoso.
Galería de imágenes
-
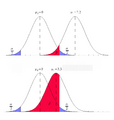
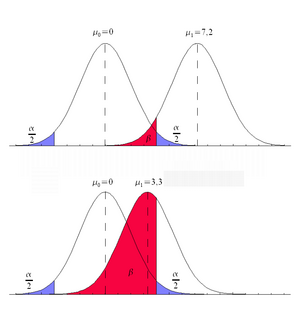
Representación de los valores posibles de la probabilidad de un error tipo II (rojo) en el ejemplo de un test de significancia estadística para el parámetro μ. El error tipo II depende del parámetro μ. Cuanto más cerca se encuentre este del valor supuesto bajo la hipótesis nula, mayor es la probabilidad de ocurrencia del error tipo II.
Véase también
 En inglés: Type I and type II errors Facts for Kids
En inglés: Type I and type II errors Facts for Kids
Enlaces externos
de:Fehler#Statistik