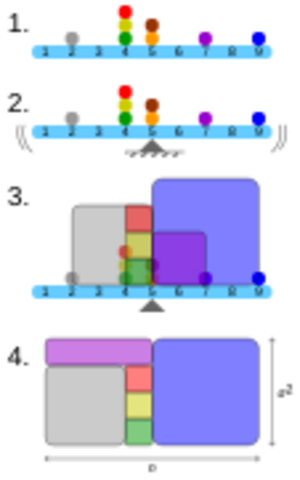
Varianza para niños
La varianza es un concepto importante en estadística que nos ayuda a entender qué tan dispersos o separados están los datos en un grupo. Imagina que tienes un grupo de números, como las alturas de tus compañeros de clase. La varianza te dice si esas alturas son muy parecidas entre sí o si hay mucha diferencia entre la persona más alta y la más baja.
Se representa con el símbolo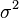 
(que se lee "sigma al cuadrado"). La unidad de medida de la varianza siempre será el cuadrado de la unidad de los datos originales. Por ejemplo, si mides alturas en metros, la varianza se expresará en metros cuadrados. La varianza siempre es un número igual o mayor que cero.
Existe una medida muy relacionada llamada desviación estándar, que es la raíz cuadrada de la varianza. La desviación estándar es más fácil de entender porque se expresa en las mismas unidades que los datos originales.
Es importante saber que la varianza puede verse muy afectada por los "valores atípicos". Estos son números que están muy lejos del resto de los datos. Si hay valores atípicos, la varianza podría no dar una imagen precisa de la dispersión.
Hay dos formas principales de entender la varianza:
- La varianza de una población: Se calcula cuando tienes todos los datos posibles de un grupo.
- La varianza de una muestra: Se calcula cuando solo tienes una parte de los datos de un grupo grande. Esta se usa para estimar la varianza de toda la población.
Contenido
¿Quién inventó el término "Varianza"?
El término varianza fue usado por primera vez por un científico llamado Ronald Fisher. Lo mencionó en un artículo que publicó en enero de 1919. Él explicó que, para entender la variabilidad de algo, era útil usar el cuadrado de la desviación típica. A esa cantidad la llamó "Varianza".
¿Qué es la Varianza?
La varianza de un grupo de datos es el promedio de las distancias al cuadrado de cada dato con respecto a la media (el promedio) de ese grupo. En otras palabras, mide cuánto se aleja cada número del promedio, pero elevando esa diferencia al cuadrado.
La fórmula general para la varianza de una variable 
es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{Var}(X) = \operatorname{E}\left[(X - \mu)^2 \right].
Aquí,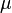 
(que se lee "mu") es la media de los datos.
Una forma más sencilla de ver la fórmula es:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{Var}(X) = \operatorname{E}\left[X^2 \right] - \operatorname{E}[X]^2
Esto significa que la varianza es igual al promedio de los datos al cuadrado, menos el cuadrado del promedio de los datos.
Cómo se calcula la Varianza
La unidad de medida de la varianza siempre será la unidad de los datos originales, pero elevada al cuadrado. La varianza siempre es un número igual o mayor que cero. Esto es porque las diferencias se elevan al cuadrado, y cualquier número al cuadrado (positivo o negativo) siempre resulta en un número positivo.
Varianza para datos continuos
Si tienes datos que pueden tomar cualquier valor dentro de un rango (como la altura o el peso), la varianza se calcula usando una integral. Esto es una operación matemática avanzada que suma todas las pequeñas partes de una función.
Varianza para datos discretos
Si tienes datos que solo pueden tomar valores específicos (como el número de caras al lanzar una moneda), la varianza se calcula sumando las diferencias al cuadrado de cada valor con respecto a la media, multiplicadas por la probabilidad de que ocurra cada valor.
Propiedades importantes de la Varianza
La varianza tiene algunas propiedades útiles:
- La varianza siempre es mayor o igual que cero:
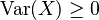. - La varianza de un número fijo (que no cambia) es cero:
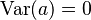. - Si multiplicas todos tus datos por un número, la varianza se multiplica por el cuadrado de ese número:
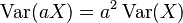. - Si sumas dos grupos de datos que no están relacionados entre sí, la varianza total es la suma de sus varianzas individuales:
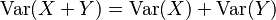(si e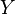 
son independientes).
Ejemplos de Varianza
Lanzar una moneda
Imagina que lanzas una moneda. Podemos darle un valor de 0 a "Cara" y 1 a "Cruz".
- Los posibles resultados son: {0, 1}.
- Si lanzas la moneda muchas veces, la media de los resultados será 0.5 (la mitad serán caras y la mitad cruces).
- La varianza te dirá qué tan dispersos están estos resultados alrededor de 0.5.
Lanzar un dado
Si lanzas un dado de seis caras, los valores posibles son del 1 al 6. Cada número tiene la misma probabilidad de salir (1/6).
- La media de los resultados es (1+2+3+4+5+6)/6 = 3.5.
- Para calcular la varianza, haríamos lo siguiente:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{i=1}^6 \tfrac{1}{6} (i - 3,5)^2 = \tfrac{1}{6}\left((-2,5)^2{+}(-1,5)^2{+}(-0,5)^2{+}0,5^2{+}1,5^2{+}2,5^2\right) = \tfrac{1}{6} \cdot 17,50 \approx 2,92\,.
Esto significa que los resultados de lanzar un dado tienen una dispersión de aproximadamente 2.92 alrededor de la media de 3.5.
Varianza de una muestra
Cuando no podemos obtener todos los datos de una población (por ejemplo, la altura de todos los adolescentes del mundo), tomamos una muestra (un grupo más pequeño). A partir de esa muestra, podemos estimar la varianza de toda la población.
Existen dos fórmulas comunes para calcular la varianza de una muestra:
- Una fórmula divide por
(el número de datos en la muestra):
:
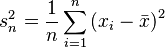
- Otra fórmula divide por
:
:
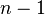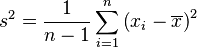La fórmula que divide por 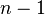es la más usada porque da una estimación más precisa de la varianza de la población, especialmente cuando la muestra es pequeña.
Usos de la Varianza
La varianza es una herramienta muy útil en estadística y tiene muchas aplicaciones:
- Estimadores eficientes: Ayuda a encontrar las mejores formas de estimar valores desconocidos, asegurando que nuestras estimaciones sean lo más cercanas posible a la realidad.
- Estimadores consistentes: Nos dice que, si tomamos muestras cada vez más grandes, nuestra estimación de la varianza se acercará mucho al valor real.
- Distribución normal: En la famosa "campana de Gauss" (distribución normal), la varianza (o su raíz cuadrada, la desviación típica) es clave para saber qué tan ancha o estrecha es la campana. Una varianza pequeña significa una campana alta y estrecha, con datos muy juntos.
- Análisis de la varianza (ANOVA): Es una técnica que usa la varianza para comparar si hay diferencias importantes entre las medias de varios grupos. Por ejemplo, para ver si un nuevo método de estudio mejora las calificaciones de un grupo de estudiantes comparado con otro grupo.
- Análisis de riesgo: En áreas como las finanzas, la varianza se usa para medir el riesgo de una inversión. Una varianza alta significa que los resultados pueden variar mucho, lo que implica un mayor riesgo.
Conclusión
La varianza es una medida fundamental en estadística que nos ayuda a entender la dispersión de los datos. Nos dice qué tan separados están los valores de un conjunto con respecto a su promedio. Aunque es sensible a los valores atípicos (datos muy diferentes al resto), es una herramienta poderosa para analizar y comparar grupos de información. Junto con la desviación estándar, nos permite tener una idea clara de la vari variabilidad en diferentes situaciones, desde el lanzamiento de un dado hasta el análisis de datos complejos.
Véase también
En inglés: Variance Facts for Kids
- Desviación típica
- Esperanza matemática
- Análisis de varianza
