Politopo regular para niños

En matemáticas, un politopo regular es una forma geométrica con mucha simetría. Imagina una figura que se ve igual desde muchos ángulos.

Algunos ejemplos de politopos regulares en dos dimensiones son el cuadrado, el pentágono y el hexágono regular. En tres dimensiones, encontramos los sólidos platónicos (que son poliedros regulares). También existen ejemplos en dimensiones más altas. Los círculos y las esferas, aunque son muy simétricos, no se consideran politopos porque no tienen caras planas. La gran simetría de los politopos regulares los hace muy atractivos para los matemáticos.

Muchos politopos regulares se encuentran en la naturaleza y se conocen desde hace mucho tiempo. Los primeros estudios matemáticos de estas formas vienen de los antiguos griegos, como Euclides. Él escribió un libro llamado Elementos de Euclides, donde explicó la geometría y la teoría de los números. Su trabajo terminó con descripciones matemáticas de los cinco sólidos Platónicos.

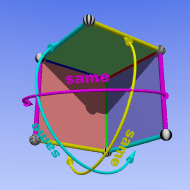
La definición de los politopos regulares no cambió por muchos siglos después de Euclides. Sin embargo, con el tiempo, esta definición se hizo más amplia. Así, se incluyeron más tipos de objetos. A los cinco sólidos Platónicos se unieron, a mediados del siglo XV, los poliedros de Kepler-Poinsot. A finales del siglo XIX, los matemáticos comenzaron a estudiar politopos regulares en cuatro o más dimensiones, como el teseracto (también llamado hipercubo) y el 24cell. Aunque el 24-cell es difícil de imaginar, mantiene la belleza simétrica de sus "primos" de menos dimensiones. Aún más difíciles de visualizar son los politopos regulares abstractos modernos, como el 57cell o el 11cell. Los matemáticos que los estudian aseguran que estos objetos también tienen una gran belleza.

¿Cómo se descubrieron los politopos regulares?

Orígenes antiguos

Se cree que los antiguos matemáticos griegos fueron los primeros en descubrir los poliedros regulares. Los primeros escritos sobre ellos provienen de autores griegos, quienes también hicieron las primeras descripciones matemáticas.

Sin embargo, en el mar Mediterráneo, la civilización etrusca parece haber conocido al menos uno de estos poliedros regulares antes que los griegos. Cerca de Padua, en el norte de Italia, se encontró un dodecaedro de piedra jabón de hace más de 2500 años. Algunos creen que su forma se inspiró en el "piritoedro", un mineral común en esa región.

Aún antes que los etruscos, en Escocia se encontraron piedras talladas con formas que muestran la simetría de los cinco sólidos platónicos. Estas piedras tienen unos 4,000 años de antigüedad. No solo muestran la forma de cada sólido, sino también cómo se relacionan entre sí (por ejemplo, que los centros de las caras de un cubo forman los vértices de un octaedro). Puedes ver ejemplos de estas piedras en el Ashmolean Museum de la Universidad de Oxford. No sabemos por qué se hicieron estos objetos ni qué inspiró a los escultores.

No hay pruebas de que los etruscos o los antiguos escoceses tuvieran un conocimiento matemático profundo de los sólidos regulares. Sin embargo, el estudio que los antiguos griegos hicieron de los sólidos platónicos es lo que ha llegado hasta nosotros y ha impulsado las matemáticas modernas.

La Grecia antigua y los sólidos platónicos

Algunos historiadores creen que Pitágoras (alrededor del 550 a.C.) describió los sólidos platónicos. Otros dicen que él solo conocía el tetraedro, el cubo y el dodecaedro. Se piensa que Teateto descubrió los otros dos y los describió matemáticamente (Euclides, libro XIII). H.S.M. Coxeter (1948) menciona que Platón (alrededor del 400 a.C.) ya había hecho modelos de ellos. También dice que un pitagórico temprano usó los cinco sólidos para relacionarlos con la naturaleza del universo. De Platón viene el nombre de sólidos Platónicos.

Poliedros estrella: una nueva era

Durante casi 2000 años, la idea de un politopo regular se mantuvo como la definieron los griegos. La definición griega decía:

• Un polígono regular es una figura plana convexa con lados y ángulos iguales.
• Un poliedro regular es una figura sólida convexa con caras que son polígonos regulares iguales. Además, el mismo número de polígonos se unen en cada vértice.

Esta definición no incluye, por ejemplo, una pirámide cuadrada. Aunque todas sus caras son regulares, la base cuadrada no es igual a los lados triangulares.

Finalmente, a principios del siglo XV, surgieron nuevos tipos de politopos regulares. Los poliedros estrellados regulares se llaman sólidos de Kepler-Poinsot, en honor a Johannes Kepler y Louis Poinsot. Estas figuras tienen polígonos regulares que no son convexos, como los pentagramas. Kepler fue el primero en ver que estas formas podían considerarse "regulares" si se eliminaba la regla de que los politopos debían ser convexos. Más tarde, Poinsot descubrió los dos que faltaban.

Los poliedros de Kepler-Poinsot se pueden crear a partir de los sólidos platónicos mediante un proceso llamado estrellamiento. El estudio de los estrellamientos de los sólidos platónicos cobró fuerza gracias a H.S.M. Coxeter y otros en 1938, con el famoso artículo El icosaedro 59.

El proceso opuesto al estrellamiento es el facetado. Cada estrellamiento de un politopo es el "dual" (o recíproco) de algún facetado del politopo dual. Los poliedros regulares estrellados también se pueden obtener al facetar los sólidos platónicos.

Politopos de más dimensiones

No fue hasta el siglo XIX cuando un matemático suizo, Ludwig Schläfli, estudió y describió los politopos regulares de más dimensiones. Sus trabajos se publicaron por completo seis años después de su muerte (Schläfli, 1901). Entre 1880 y 1900, otros nueve matemáticos redescubrieron los resultados de Schläfli de forma independiente.

Schläfli demostró que existen seis politopos regulares convexos en cuatro dimensiones. Sin embargo, solo hay tres cuando las dimensiones son cinco o más (las versiones más grandes del tetraedro, cubo y octaedro). También son interesantes los politopos estrellados de cuatro dimensiones, que Schläfli no descubrió.

A principios del siglo XX, la definición de un politopo regular se estableció así:

• Un polígono regular tiene todos sus lados y ángulos iguales.
• Un poliedro regular tiene caras que son polígonos regulares iguales. Además, todas sus figuras de vértice son iguales y regulares.
• De manera similar, un n-politopo regular es una figura n-dimensional donde todas sus "caras" (de n−1 dimensiones) son regulares e iguales. También, sus "figuras de vértice" son todas regulares e iguales.

Esta es una definición "recursiva". Define la regularidad de figuras de dimensiones superiores basándose en figuras regulares de una dimensión inferior. Hay otra definición que dice que un politopo es regular si tiene un alto grado de simetría.

• Un n-politopo es regular si cualquier combinación de un vértice, un lado que lo contiene, una cara bidimensional que contiene a ambos, y así hasta n − 1 dimensiones, puede ser movida a cualquier otra combinación similar mediante una simetría del politopo.

Por ejemplo, el cubo es regular. Si eliges un vértice, uno de los tres lados que lo tocan y una de las dos caras que contienen ese lado, esta combinación (vértice, lado, cara) puede ser movida a cualquier otra combinación similar usando una simetría del cubo.

Politopos regulares abstractos

En el siglo XX, hubo avances importantes. Los grupos de simetría de los politopos regulares clásicos se hicieron más generales. Ahora se les llama grupos de Coxeter. Estos grupos también incluyen las simetrías de los patrones que cubren el espacio o un plano, como un tablero de ajedrez infinito.

En los años 1960, Branko Grünbaum animó a los matemáticos a estudiar más tipos de politopos regulares abstractos, a los que llamó polistrómatas. Él desarrolló la teoría de los polistrómatas y mostró ejemplos de nuevos objetos, como los apeirotopos regulares. Estos son politopos regulares con un número infinito de caras. Un ejemplo sencillo de un apeirógono es un zig-zag. Cumple la definición de un polígono regular: todos los lados tienen la misma longitud y todos los ángulos son iguales. Además, tiene simetrías que permiten dividir la figura en dos partes iguales desde cualquier vértice.

Grünbaum también descubrió el 11-cell, un hermoso poliedro de cuatro dimensiones que es "autodual" (su dual es él mismo). El 11-cell es un objeto cuyas caras no son icosaedros, sino hemicosaedros. Un hemicosaedro es como un icosaedro donde las caras opuestas se consideran la misma cara (Grünbaum, 1977). El hemicosaedro tiene solo 10 caras triangulares y 6 vértices, a diferencia del icosaedro, que tiene 20 y 12.

Este concepto es más fácil de entender si piensas en la relación entre un cubo y un hemicubo. Un cubo normal tiene 8 vértices, que podríamos llamar de A a H. En un hemicubo, A y H se consideran el mismo vértice, y lo mismo ocurre con B y G, y los demás. La arista AB sería la misma que GH, y la cara ABEF la misma que CDGH. La nueva forma tiene solo tres caras, 6 aristas y 4 vértices.

Pocos años después del descubrimiento del 11-cell por Grünbaum, H.S.M. Coxeter lo descubrió de forma independiente. Antes, Coxeter había encontrado un politopo similar, el 57-cell (Coxeter, 1982, 1984).

El estudio de los polistrómatas fue menos popular cuando los matemáticos se interesaron por otros conceptos abstractos, como los edificios y geometrías, politopos abstractos y conjuntos de Euler. El 11-cell y el 57-cell siguen siendo ejemplos importantes de politopos abstractos regulares.

Un politopo regular abstracto se define como un conjunto que representa los vértices, lados y caras de un politopo. Se establecen ciertas reglas para estos conjuntos, similares a las propiedades de los politopos regulares clásicos (como los sólidos platónicos). Sin embargo, las reglas son lo suficientemente flexibles como para incluir patrones regulares, hemicubos, y objetos más extraños como el 11-cell. Esta teoría fue desarrollada principalmente por Egon Schulte y Peter McMullen (McMullen, 2002), con contribuciones de otros investigadores.

¿Cómo se construyen los politopos?

Polígonos

La forma tradicional de construir un polígono regular o cualquier otra figura plana es usando una regla y compás. Construir algunos polígonos regulares es muy fácil (el triángulo equilátero es uno de los más sencillos). Otros son más difíciles o imposibles de construir. Los polígonos regulares más simples que no se pueden construir con regla y compás son los de n lados, donde n es 7, 9, 11, 13, 14, 18, 19, 21, y así sucesivamente.

Poliedros

Los Elementos de Euclides (puedes verlos en Elementos en español) muestran cómo construir los cinco sólidos platónicos con regla y compás. Sin embargo, la pregunta de cómo dibujar una línea recta en el espacio, incluso con una regla, nos hace pensar qué significa realmente "construir" un poliedro regular.

En geometría, "construcción" significa seguir un procedimiento para crear algo. La forma más común de construir un poliedro regular es mediante un "despliegue" o "desdoblamiento". Para obtener el desdoblamiento de un poliedro, se corta su superficie a lo largo de suficientes aristas para que pueda quedar plana. Esto crea un plano del poliedro desplegado. Como las caras de los sólidos platónicos son solo triángulos, cuadrados y pentágonos, y todos estos polígonos se pueden construir con regla y compás, existen métodos para dibujar estos desdoblamientos. Lo mismo aplica a los poliedros de Kepler.

Si dibujas el desdoblamiento en cartón o un material flexible, puedes cortarlo, doblarlo por los lados que no cortaste y unir los lados cortados para formar el poliedro. Un poliedro puede tener muchos desdoblamientos. Por ejemplo, el cubo tiene 11, y el dodecaedro tiene más de 40,000. Puedes ver algunos desdoblamientos interesantes del cubo, octaedro, dodecaedro e icosaedro aquí.

Muchos juguetes para niños, especialmente para preadolescentes y adolescentes, permiten experimentar con polígonos y poliedros regulares. Por ejemplo, klikko ofrece conjuntos de triángulos, cuadrados, pentágonos y hexágonos de plástico que se pueden unir de muchas maneras. Estos juguetes permiten a los niños redescubrir los sólidos platónicos (o los sólidos arquimedeanos), sobre todo si un adulto con conocimientos los guía.

En teoría, los poliedros regulares se pueden construir con casi cualquier material. Aquí, por ejemplo, hay instrucciones para construir modelos usando técnicas de origami. También se pueden tallar en madera, hacer con alambre o con cristal emplomado. ¡La imaginación es el límite!

Dimensiones superiores

Cuando pasamos a dimensiones mayores, es más difícil saber qué significa "construir" estos objetos. En un universo tridimensional, es imposible construir un modelo físico de un objeto de cuatro dimensiones. Hay varias formas de abordar este problema.

El primer método es representar el objeto de dimensiones superiores en el espacio tridimensional. Esto se hace de manera similar a cómo representamos objetos tridimensionales en un plano. Por ejemplo, los desdoblamientos que mencionamos antes tienen equivalentes en dimensiones superiores. Podrías imaginar construir un modelo de este desdoblamiento, como dibujas el desdoblamiento de un poliedro en papel. Lamentablemente, no podrás doblar la estructura para obtener un politopo de cuatro dimensiones, debido a las limitaciones de nuestro universo físico. Otra forma de "dibujar" formas de dimensiones superiores en tres dimensiones es mediante algún tipo de proyección, como las análogas a la proyección ortográfica o la perspectiva gráfica. El famoso libro de Coxeter sobre politopos (Coxeter, 1948) tiene ejemplos de estas proyecciones ortográficas. Puedes encontrar más ejemplos en la web. Ten en cuenta que representar objetos de cuatro dimensiones directamente en dos dimensiones es muy confuso. Los modelos tridimensionales de las proyecciones son más fáciles de entender; a veces se encuentran en museos de ciencia o departamentos de matemáticas de universidades.

La intersección de un politopo regular de cuatro dimensiones con un hiperplano tridimensional será un politopo (no siempre regular). Al mover el hiperplano a través de la forma, las "rebanadas" tridimensionales se pueden combinar y animar en una especie de objeto de cuatro dimensiones, donde la cuarta dimensión sería el tiempo. De esta manera, a través de estos cortes, podemos ver (aunque no entender completamente) la estructura completa en cuatro dimensiones de un politopo regular de cuatro dimensiones. Este método es similar a cómo un tomógrafo axial computado une imágenes bidimensionales para crear una representación de los órganos. Lo ideal sería un holograma animado; sin embargo, incluso una animación simple como la que se muestra puede dar una idea limitada de la estructura del politopo.

Otra forma en que una persona tridimensional puede entender la estructura de un objeto de cuatro dimensiones es "sumergiéndose" en él, quizás con tecnología de realidad virtual. Para entender cómo funcionaría esto, imagina que el espacio estuviera lleno de cubos. Estarías dentro de uno de ellos y podrías ver cubos delante, detrás, arriba, abajo, a la izquierda y a la derecha. Si pudieras viajar en esas direcciones, podrías explorar la disposición de los cubos y entender su estructura geométrica. Una disposición infinita de cubos no es un politopo en el sentido tradicional. Es una división del espacio euclidiano tridimensional. Sin embargo, un politopo de cuatro dimensiones puede verse como un patrón que cubre un espacio no euclidiano tridimensional, es decir, la superficie de una esfera de cuatro dimensiones. Localmente, este espacio se vería como el que conocemos. Por lo tanto, en principio, se podría programar un sistema de realidad virtual para explorar estos "patrones", es decir, los politopos regulares de cuatro dimensiones. El departamento de matemáticas de la UIUC tiene imágenes de lo que se vería si un observador estuviera en un patrón de espacio hiperbólico con dodecaedros. Este patrón es un ejemplo de un politopo regular abstracto infinito.

Normalmente, para los politopos regulares abstractos, un matemático considera que el objeto está "construido" si se conoce la estructura de su grupo de simetría. Esto se debe a que un teorema importante en el estudio de los politopos regulares abstractos permite construir el politopo regular abstracto a partir de su grupo de simetría de una manera directa y estándar.

Politopos en la naturaleza

Polígonos

En la naturaleza se pueden observar muchos polígonos regulares. En el mundo de los minerales, los cristales a menudo tienen caras triangulares, cuadradas o hexagonales. Los cuasicristales incluso pueden tener caras en forma de pentágonos regulares. Otro ejemplo fascinante de polígonos regulares creados por procesos geológicos se ve en la Calzada de los Gigantes en Irlanda, o en la Devil's Postpile en California. Allí, el enfriamiento de la lava ha formado áreas de columnas hexagonales de basalto muy unidas.

Carambola, una fruta popular del Sureste de Asia.

Los hexágonos más famosos en la naturaleza se encuentran en el reino animal. Los panales de abejas son un conjunto de hexágonos que usan para guardar miel y polen, y para que crezcan las larvas. También hay animales que tienen una forma parecida a polígonos regulares (o al menos la misma simetría). Por ejemplo, la estrella de mar y a veces otros equinodermos como el erizo de mar, muestran la simetría de un pentágono u otros polígonos. Las medusas suelen tener simetría cuádruple (como un cuadrado) u óctuple.

La simetría radial (y otras simetrías) también se ve mucho en el reino vegetal, especialmente en las flores, y en menor medida en las semillas y frutas. Las formas pentagonales son las más comunes. Un ejemplo notable es la carambola (Averrhoa carambola), una fruta del sudeste asiático. Si la cortas, tiene forma de estrella pentagonal.

Pasando de la Tierra al espacio, matemáticos pioneros usaron la ley de gravitación de Newton. Descubrieron que si dos cuerpos (como el Sol y la Tierra) orbitan uno alrededor del otro, hay puntos en el espacio donde un cuerpo más pequeño (como un asteroide o una estación espacial) se mantendrá en una órbita estable. Estos puntos se llaman puntos de Lagrange. El sistema Sol-Tierra tiene cinco puntos de Lagrange. Los dos más estables están exactamente 60° delante y detrás de la Tierra en su órbita. Esto significa que si unes los centros del Sol, la Tierra y uno de esos puntos, se forma un triángulo equilátero. Los astrónomos ya han encontrado asteroides troyanos en esos puntos. Ya hay satélites y sondas espaciales en los puntos de Lagrange menos estables, que no forman un triángulo equilátero con la Tierra y el Sol. Se han usado principalmente para observar el Sol, y la sonda más famosa en uno de esos puntos ha sido la SOHO.

Poliedros

Los seres humanos no fueron los primeros en construir sólidos platónicos. Todos ellos aparecen de forma natural, aunque no siempre son fáciles de ver. El tetraedro, el cubo y el octaedro aparecen como cristales. Sin embargo, los cristales pueden tener 48 formas diferentes (Smith, 1982). Ni los icosaedros regulares ni los dodecaedros regulares se encuentran entre ellas. Aunque una de las formas, el piritoedro (llamado así por el grupo de piritas), tiene doce caras pentagonales, dispuestas como un dodecaedro regular. Pero sus caras son irregulares, por lo que el piritoedro no es regular.

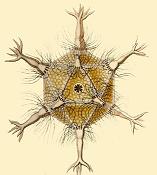
A principios del siglo XX, Ernst Haeckel (1904) describió varias especies de Radiolaria cuyos esqueletos tienen forma de diversos poliedros regulares. Ejemplos incluyen Circoporus octahedrus, Circogonia icosahedra, Lithocubus geometricus y Circorrhegma dodecahedra. Las formas de estas criaturas son claras por sus nombres.

Un descubrimiento más reciente es el de un nuevo tipo de moléculas de carbono, conocidas como fulerenos (puedes encontrar una explicación sencilla en (Curl, 1991)). Aunque el C₆₀, el fulereno más fácil de producir, parece más o menos esférico, se cree que algunas de las variedades más grandes (como C₂₄₀, C₄₈₀ y C₉₆₀) tienen una forma ligeramente parecida a icosaedros redondeados, de unos pocos nanómetros de diámetro.

Antiguamente, los pitagóricos creían que había una armonía entre los poliedros regulares y las órbitas de los planetas. En el siglo XVII, Johannes Kepler estudió los datos del movimiento planetario de Tycho Brahe. Durante una década, intentó encontrar una relación entre los tamaños de los poliedros y los tamaños de las órbitas de los planetas. Su búsqueda no logró su objetivo principal. Sin embargo, como resultado de estas investigaciones, Kepler descubrió que los sólidos que hoy llamamos "de Kepler" son politopos regulares. También descubrió que las órbitas de los planetas no son círculos, y formuló las leyes del movimiento planetario por las que se hizo famoso. En la época de Kepler, solo se conocían cinco planetas además de la Tierra, un número igual al de los sólidos platónicos. El trabajo de Kepler y el descubrimiento posterior de los planetas Urano, Neptuno y Plutón han descartado la idea pitagórica.

Galería de imágenes

• 

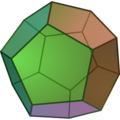
  Un dodecaedro, uno de los cinco sólidos platónicos.

Véase también

En inglés: Regular polytope Facts for Kids

• Sólidos platónicos
• H. S. M. Coxeter