Leyes de Kepler para niños

Representación gráfica de las leyes de Kepler. El Sol está situado en uno de los focos. En tiempos iguales, las áreas barridas por el planeta son iguales. Por lo tanto, el planeta se moverá más rápidamente cerca del Sol.

Las leyes de Kepler fueron enunciadas por Johannes Kepler para describir matemáticamente el movimiento de los planetas en sus órbitas alrededor del Sol.

Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas. El Sol se encuentra en uno de los focos de la elipse.

El radio vector que une un planeta y el Sol recorre áreas iguales en tiempos iguales.

La ley de las áreas es equivalente a la constancia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio).

El afelio y el perihelio son los dos únicos puntos de la órbita en los que el radio vector y la velocidad son perpendiculares. Por ello solo en esos 2 puntos el módulo del momento angular

L

se puede calcular directamente como el producto de la masa del planeta por su velocidad y su distancia al centro del Sol.

L = m \cdot r_a \cdot v_a = m \cdot r_p \cdot v_p \,

En cualquier otro punto de la órbita distinto del Afelio o del Perihelio el cálculo del momento angular es más complicado, pues como la velocidad no es perpendicular al radio vector, hay que utilizar el producto vectorial

\mathbf L = m \cdot \mathbf r \times \mathbf v\,

Para cualquier planeta, el cuadrado de su período orbital es directamente proporcional al cubo de la longitud del semieje mayor de su órbita elíptica.

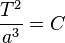
\frac{T^2}{a^3}=C=\text{constante}

Donde, T es el período orbital (tiempo que tarda en dar una vuelta alrededor del Sol), a la distancia media del planeta con el Sol y C la constante de proporcionalidad.

Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria, como el sistema formado por la Tierra y el sol.

Contenido

Formulación de Newton de la tercera ley de Kepler
Deducción matemática de las leyes de Kepler a partir de las leyes de Newton
- Demostración de la segunda ley de Kepler
- Demostración de la primera ley de Kepler

Formulación de Newton de la tercera ley de Kepler

Antes de que se redactaran las leyes de Kepler hubo otros científicos como Claudio Ptolomeo, Nicolás Copérnico y Tycho Brahe cuyas principales contribuciones al avance de la ciencia estuvieron en haber conseguido medidas muy precisas de las posiciones de los planetas y de las estrellas. Kepler, que fue discípulo de Tycho Brahe, aprovechó todas estas mediciones para poder formular su tercera ley.

Kepler logró describir el movimiento de los planetas. Utilizó los conocimientos matemáticos de su época para encontrar relaciones entre los datos de las observaciones astronómicas obtenidas por Tycho Brahe y con ellos logró componer un modelo heliocéntrico del universo. Comenzó trabajando con el modelo tradicional del cosmos, planteando trayectorias excéntricas y movimientos en epiciclos, pero encontró que los datos de las observaciones lo situaban fuera del esquema que había establecido Copérnico, lo que lo llevó a concluir que los planetas no describían una órbita circular alrededor del Sol. Ensayó otras formas para las órbitas y encontró que los planetas describen órbitas elípticas, las cuales tienen al Sol en uno de sus focos. Analizando los datos de Brahe, Kepler también descubrió que la velocidad de los planetas no es constante, sino que el radio vector que une al Sol (situado en uno de los focos de la trayectoria elíptica) con un planeta determinado, describe áreas iguales en tiempos iguales. En consecuencia, la velocidad de los planetas es mayor cuando están próximos al Sol (perihelio) que cuando se mueven por las zonas más alejadas (afelio). Esto da origen a las tres Leyes de Kepler sobre el movimiento planetario.

Las leyes de Kepler representan una descripción cinemática del sistema solar.

Primera Ley de Kepler: Todos los planetas se mueven alrededor del Sol siguiendo órbitas elípticas. El Sol está en uno de los focos de la elipse.

Segunda Ley de Kepler: Los planetas se mueven con velocidad areolar constante. Es decir, el vector posición r de cada planeta con respecto al Sol barre áreas iguales en tiempos iguales.

Se puede demostrar que el momento angular es constante lo que nos lleva a las siguientes conclusiones:

Las órbitas son planas y estables.

Se recorren siempre en el mismo sentido.

La fuerza que mueve los planetas es central.

Tercera Ley de Kepler: Se cumple que para todos los planetas, la razón entre el periodo de revolución al cuadrado y el semieje mayor de la elipse al cubo se mantiene constante. Esto es:

\frac{T^2}{a^3}=C

Ilustración de la relación entre el radio orbital y el período orbital.

El estudio de Newton de las leyes de Kepler condujo a su formulación de la ley de la gravitación universal.

La formulación matemática de Newton de la tercera ley de Kepler para órbitas circulares es:

La fuerza gravitacional crea la aceleración centrípeta necesaria para el movimiento circular de radio a:

\frac{GMm}{a^2} = m \omega^2a

recordando la expresión que relaciona la velocidad angular y el período de revolución:

\omega=\frac{2 \pi}{T}

de donde se deduce que el cuadrado del tiempo de una órbita completa o periodo es:

T^2=\frac{4\pi^2}{GM}a^3

y despejando:

\frac{T^2}{a^3}=\frac{4\pi^2}{GM}=C

donde $C$ es la constante de Kepler, T es el periodo orbital, a el semieje mayor de la órbita, M es la masa del cuerpo central y G una constante denominada Constante de gravitación universal cuyo valor marca la intensidad de la interacción gravitatoria y el sistema de unidades a utilizar para las otras variables de esta expresión. Esta expresión es válida tanto para órbitas circulares como elípticas.

En realidad, esta última expresión es solo una aproximación de la expresión más general que se deduce con todo rigor de las Leyes de Newton y que es:

\frac{T^2}{a^3} \ (M+m)=\frac{4\pi^2}{G}

Donde $M$ es la masa del cuerpo central, $m$ la del astro que gira en torno a él y $a$ sería el semieje mayor con respecto al centro de masas del sistema. Como en el Sistema Solar la masa del Sol es muy superior a la de cualquier planeta, $m \ll M$ , la expresión simplificada se obtiene de la más general haciendo $M+m \simeq M$

Deducción matemática de las leyes de Kepler a partir de las leyes de Newton

La demostración de la primera y segunda ley de Kepler se basa en las leyes de Newton y la ley de gravitación universal.

Sistema de referencia de coordenadas polares

Demostración de la segunda ley de Kepler

Enunciado matemático

Sean ${[t_1,t_2]}$ , ${[t_3,t_4]}$ dos intervalos de tiempo tal que ${t_2-t_1 = t_4-t_3}$ y sea $A_{\theta_1,\theta_2}={1 \over 2} \int\limits_{\theta_1}^{\theta_2} r^2(\theta) d\theta$ , $\forall \theta_1, \theta_2$ .

Entonces, ${A(t_2-t_1)=A(t_4-t_3)}$ .

En primer lugar, se fija un sistema de referencia de coordenadas polares:

{\textstyle \overrightarrow{x}(t)=r(t)\cdot(cos(\theta(t)),sen(\theta(t)))}

\overrightarrow{u_r}(t)=(cos(\theta(t)),sen(\theta(t)))

\overrightarrow{u_\theta}(t)=(-sen(\theta(t)),cos(\theta(t)))

donde $\overrightarrow{x}(t)$ denota la posición del cuerpo con masa $m$ en el instante $t$ ; el cuerpo con masa $M$ está quieto y en el origen; y $\overrightarrow{u_r}$ y $\overrightarrow{u_\theta}$ son vectores unitarios en las direcciones radial y circunferencial, respectivamente; y $\theta(t)$ es el ángulo que forma $r(t)$ con el eje polar (eje de referencia desde el que se mide el ángulo polar).

$\overrightarrow{u_r}$ y $\overrightarrow{u_\theta}$ satisfacen las siguientes propiedades:

{d\overrightarrow{u_r} \over d\theta}=\overrightarrow{u_\theta}

;

\quad {d\overrightarrow{u_r} \over dt}=\overrightarrow{u_r}'=\overrightarrow{u_\theta}\theta'

;

\quad \overrightarrow{u_r} \bot \overrightarrow{u_\theta}

La fuerza $\overrightarrow{F}$ sobre el cuerpo de masa $m$ se descompone en: $\overrightarrow{F}=F_r\overrightarrow{u_r}+F_\theta\overrightarrow{u_\theta}$ . Además, como $\overrightarrow{F}$ es una fuerza central, $F_\theta\equiv0$ .

Por lo tanto, aplicando la segunda ley de Newton,

F_r\overrightarrow{u_r}=\overrightarrow{F}=m\overrightarrow{x}''(t)

[1]

La velocidad del planeta es la derivada de la posición:

x'(t)=r'(t)\overrightarrow{u_r}+r(t)\theta ' (t)\overrightarrow{u_\theta}

[2]

y su aceleración es la derivada de la velocidad:

{\textstyle \begin{align} x''(t) & = r''(t)\overrightarrow{u_r}+r'(t)\theta' (t)\overrightarrow{u_\theta}+r'(t)\theta' (t)\overrightarrow{u_\theta}+r(t)\theta'' (t)\overrightarrow{u_\theta}-r(t)\theta' (t) \theta' (t)\overrightarrow{u_r} \\ & = (r''(t)-r(t)(\theta' (t))^2)\overrightarrow{u_r}+(2r'(t)\theta' (t)+r(t)\theta'' (t))\overrightarrow{u_\theta}. \\ \end{align}}

[3]

Usando $[1]$ y $[3]$ :

\begin{cases} F_r=[r''(t)-r(t)(\theta' (t))^2]m \\ 0=2r'(t)\theta' (t)+r(t)\theta''(t) \end{cases}

$\begin{matrix} [4] \\ {[5]} \end{matrix}$

Multiplicando por $r$ a ambos lados de $[5]$ :

0=2r(t)r'(t)\theta' (t)+r^2(t)\theta'' (t)=(r^2(t))'\theta' (t)+ r^2(t)\theta'' (t)=(r^2(t)\theta' (t))'

Así que $r^2(t)\theta'(t)=c$ (constante). $[6]$

Representación del área del sector barrido entre los ángulos

\theta_1

\theta_2

Por otra parte, sea $A_{\theta_1,\theta_2}$ el área del sector barrido entre los ángulos $\theta_1$ y $\theta_2$ :

A_{\theta_1,\theta_2}={1 \over 2} \textstyle \int\limits_{\theta_1}^{\theta_2} \displaystyle r^2(\theta) d\theta

Tomemos $\theta_1=0$ por simplicidad y denotemos $A_{\theta_1,\theta_2}=A$ .

Por el teorema fundamental del cálculo, ${dA \over d\theta}={r^2(\theta) \over 2}$ . Como $\theta$ es función de $t$ , por $[6]$ :

A'(t)={dA(\theta (t)) \over d\theta}\theta'(t)={r^2(\theta (t)) \over 2}\theta'(t)=c

(constante).

Por lo tanto, $A(t)=ct+k$ , para alguna constante $k$ .

Se obtiene: $A(t)=ct$ .

Aplicando esto a dos intervalos de tiempo de igual longitud, $[t_1, t_2]$ y $[t_3,t_4]$ :

A(t_2-t_1)=(t_2-t_1)c=(t_4-t_3)c=A(t_4-t_3)

. ■

Demostración de la primera ley de Kepler

Enunciado matemático

La trayectoria del cuerpo de masa m es una cónica.

Imponiendo que $F_r$ cumpla la ley universal de gravitación:

F_r= {-{GmM\over r^2(t)}}

[7]

Aplicando la segunda ley de Newton y la ley de gravitación universal:

\overrightarrow{x''}(t)=-\Bigl(G{M \over r^2(t)}\Bigr)\overrightarrow{u_r}

[8]

Igualando $[4]$ y $[7]$ :

-{GM \over r^2(t)} = r''(t)-r(t)(\theta'(t))^2

[9]

Despejando de la ecuación $[6]$ se obtiene: $\theta'(t)= {c \over r^2(t)}$ , para c constante. $[10]$

Se puede reescribir la ecuación $[9]$ , usando $[10]$ , como:

-{GM \over r^2(t)}=r''(t)-{c^2\over r^3(t)}

[11]

Haciendo el cambio $z(t)={1 \over r(t)}$ y derivando dos veces, obtenemos lo siguiente:

r'(t)=-{1 \over z^2(t)}z'(t)=-{1 \over z^2(t)}{dz(t) \over d\theta (t)} \theta'(t)=-c{dz(t) \over d\theta (t)}

r''(t)=-c{d \over dt}\biggl({dz(t) \over d\theta (t)}\Biggr)=-c{d^2z(t) \over d\theta^2 (t)}\theta' (t)

Usando $[10]$ :

r''(t)=-c^2z^2(t){d^2z(t) \over d\theta^2 (t)}

Sustituyendo $r''(t)$ en el lado derecho de $[11]$ :

r''(t)-{c^2 \over r^3(t)}=-c^2z^2(t){d^2z(t) \over d\theta^2 (t)}-{c^2 \over r^3(t)}=-c^2z^2(t){d^2z(t) \over d\theta^2 (t)}-c^2z^3(t)

y en el lado izquierdo aplicando de nuevo el cambio $z(t)={1 \over r(t)}$ :

-{GM \over r^2(t)}=-GMz^2(t)

De esta forma, la ecuación $[9]$ se puede escribir como:

z+{d^2z \over d\theta^2 }={GM \over c^2}

Esta ecuación diferencial tiene como únicas soluciones:

z(\theta)=Acos(\theta-\alpha)+{GM\over c^2}

, donde

A

\alpha

son constantes.

Eligiendo el eje polar de manera que $\alpha=0$ :

r(\theta)={1 \over Acos(\theta) + {GM\over c^2}}={{c^2 \over GM} \over Bcos(\theta) +1}

, donde

B={Ac^2 \over GM}

Haciendo los cambios $e=B$ y $p={1\over A}$ , se obtiene la ecuación de una cónica con foco en el origen:

r(\theta)={ep \over ecos(\theta)+1 }

, donde

e

es la excentricidad y

p

es la distancia del foco a la directriz.

Según el valor de $e$ , esta cónica puede ser una elipse, una hipérbola o una parábola.

En este caso, si la trayectoria de los cuerpos celestes está acotada, el único caso posible es que sea una elipse, $0<e<1$ . ■

Obtenido de «https://ninos.kiddle.co/index.php?title=Leyes_de_Kepler&oldid=2987902»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Leyes de Kepler para Niños. Enciclopedia Kiddle.