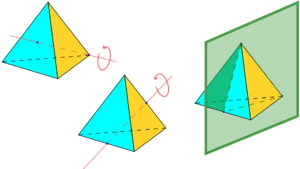
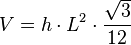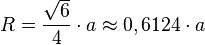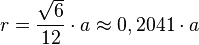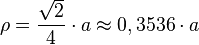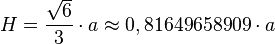Tetraedro para niños

Enciclopedia para niños

Datos para niños Tetraedro regular
Familia: Sólidos platónicos
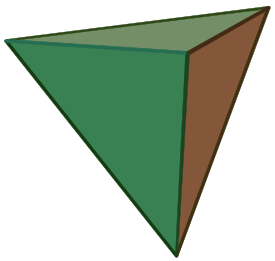Imagen del sólido
Caras	4
Aristas	6
Vértices	4
Grupo de simetría	Tetraédrico (T_d)
Poliedro dual	Tetraedro regular (autoconjugado)
Ángulo diedro	cos^-1(1/3) ≈ 70.52878°
Símbolo de Schläfli	{3, 3}
Símbolo de Wythoff	3 \| 2 3
Propiedades
Poliedro regular convexo, deltaedro

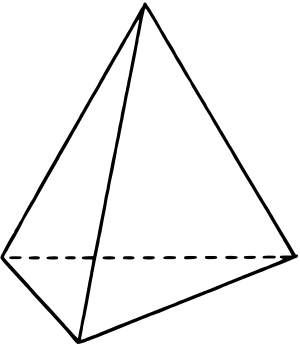
Un tetraedro es una figura geométrica en 3D. Su nombre viene del griego y significa "cuatro caras". También se le conoce como pirámide triangular.

Tiene cuatro caras, seis aristas (los bordes) y cuatro vértices (las esquinas). Todas sus caras son triángulos. En cada vértice se unen tres caras.

Si las cuatro caras de un tetraedro son triángulos equiláteros (triángulos con todos sus lados iguales), entonces se llama tetraedro regular. El tetraedro regular es uno de los sólidos platónicos, que son figuras 3D muy especiales y simétricas.

El tetraedro es el poliedro (figura 3D con caras planas) más sencillo. Es el único que tiene menos de cinco caras.

Elementos Clave del Tetraedro

Además de las caras, vértices y aristas, un tetraedro tiene otros elementos importantes.

Esferas Relacionadas con el Tetraedro

Un tetraedro puede tener esferas especiales asociadas a él:

La esfera inscrita es una esfera que está dentro del tetraedro. Toca las cuatro caras del tetraedro por dentro. Su centro está en el interior de la figura.
La esfera circunscrita es una esfera que rodea el tetraedro. Los cuatro vértices del tetraedro tocan la superficie de esta esfera. Su centro también está dentro de la figura.

Bimedianas del Tetraedro

Las bimedianas son segmentos que unen los puntos medios de dos aristas opuestas. En un tetraedro, las bimedianas se encuentran en un mismo punto. Este punto es el centro de las bimedianas.

Propiedades Geométricas del Tetraedro

Tetraedro no regular.

Los tetraedros tienen varias propiedades interesantes:

Los segmentos que unen cada vértice con el centro de las medianas de su cara opuesta se encuentran en un punto. Este punto los divide de una forma específica.
Los seis planos que son perpendiculares a las aristas por sus puntos medios se cruzan en un mismo punto. Este punto es el centro de la esfera que rodea el tetraedro.
Los planos que dividen por la mitad los ángulos entre las caras (planos bisectores) se encuentran en un punto. Este punto está a la misma distancia de las cuatro caras. Es el centro de la esfera que está dentro del tetraedro.
Un plano que pasa por una arista y el punto medio de la arista opuesta divide el tetraedro regular en dos partes iguales.
El tetraedro tiene una característica de Euler de 2.
Las bimedianas se cortan en un punto llamado centro de masas. Se dividen mutuamente por la mitad.

Cómo Calcular el Volumen del Tetraedro

El volumen es la cantidad de espacio que ocupa una figura 3D.

Fórmula General del Volumen

El volumen de cualquier tetraedro se calcula con la fórmula:

V =

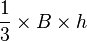
\frac{1}{3} \times B \times h

Aquí, B es el área de una de sus caras (la base) y h es la altura del tetraedro. La altura es la distancia perpendicular desde el vértice opuesto hasta el plano de la base.

Si el tetraedro tiene una base regular de lado L y altura h, su volumen es:

V = h\cdot L^2\cdot \frac{\sqrt{3}}{12}

Volumen Usando Coordenadas

Si conoces las coordenadas de los vértices de un tetraedro, puedes usar fórmulas más avanzadas para calcular su volumen. Por ejemplo, si un vértice está en el origen (0,0,0) y los otros tres son A, B y C, se usa una matriz.

También hay una fórmula que usa las coordenadas de los cuatro vértices:

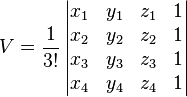
$V = \frac{1}{3!}\, \begin{vmatrix} x_1 & y_1 & z_1 & 1 \\ x_2 & y_2 & z_2 & 1 \\ x_3 & y_3 & z_3 & 1 \\ x_4 & y_4 & z_4 & 1 \end{vmatrix}$

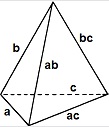
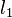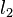Otra forma de calcular el volumen es conociendo la longitud de dos aristas opuestas ( $\ l_1$ y $\ l_2$ ), la distancia entre ellas ( 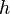$\ h$ ) y el ángulo ( 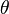$\theta$ ) que forman:

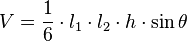
$V=\frac{1}{6} \cdot l_1 \cdot l_2 \cdot h \cdot \sin \theta$

Esta fórmula se usa para estimar el volumen de estructuras como terraplenes o presas.

Un tetraedro con sus aristas marcadas.

Alturas del Tetraedro

Un tetraedro tiene cuatro alturas, una para cada cara. La altura es la distancia perpendicular desde un vértice hasta el plano de la cara opuesta. Puedes calcular cada altura si conoces las coordenadas de los cuatro vértices.

El Tetraedro Regular: Un Sólido Especial

Un tetraedro regular es un poliedro con cuatro caras que son triángulos equiláteros idénticos. Tiene cuatro vértices, y en cada uno se unen tres caras. Es uno de los cinco sólidos platónicos, que son figuras 3D perfectas. También es un deltaedro, un poliedro con caras triangulares equiláteras.

Los antiguos pitagóricos creían que el tetraedro representaba el elemento fuego. Pensaban que las partículas de fuego tenían esta forma.

Medidas del Tetraedro Regular

Si conoces la longitud de una arista (llamada a) de un tetraedro regular, puedes calcular todas sus otras medidas:

Radio R de la esfera circunscrita: Es el radio de la esfera que toca todos los vértices del tetraedro.

R= \frac{ \sqrt{6} }{4} \cdot a \approx 0,6124 \cdot a

Radio r de la esfera inscrita: Es el radio de la esfera que toca todas las caras del tetraedro por dentro.

r=\frac{ \sqrt{6} }{12} \cdot a \approx 0,2041 \cdot a

Radio ρ de la esfera tangente a las aristas: Es el radio de una esfera que toca las seis aristas del tetraedro.

\rho = \frac{ \sqrt{2} }{4} \cdot a \approx 0,3536 \cdot a

En un tetraedro regular, las aristas opuestas (las que no se tocan en un vértice) son perpendiculares entre sí.

Altura H del tetraedro regular: Es la distancia desde una cara hasta el vértice opuesto.

H = \frac{\sqrt{6} }{3} \cdot a \approx 0,81649658909 \cdot a

Volumen, Área y Desarrollo del Tetraedro Regular

Animación de cómo se "despliega" un tetraedro.

Para un tetraedro regular con arista a:

Su volumen V se calcula con:

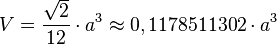
$V=\frac{\sqrt{2}}{12} \cdot a^3 \approx 0,1178511302 \cdot a^3$

El área total A de sus cuatro caras es:

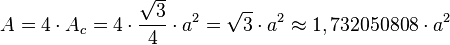
$A=4 \cdot A_c=4 \cdot \frac{\sqrt{3}}{4} \cdot a^2 = \sqrt{3} \cdot a^2 \approx 1,732050808 \cdot a^2$

Ángulos del Tetraedro Regular

Los ángulos planos de las caras son de 60°, porque son triángulos equiláteros.
Los ángulos diedros son los ángulos entre dos caras que se encuentran. En un tetraedro regular, todos son iguales:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \delta=2 \cdot \arcsin {\frac{\sqrt{3}}{3}} \approx 70^\circ 31' 43,61''

Los ángulos sólidos son los ángulos en los vértices. También son todos iguales.

Propiedades Especiales del Tetraedro Regular

Simetría

Rotaciones y reflexiones de un tetraedro regular.

Un tetraedro regular es muy simétrico. Tiene:

Cuatro ejes de simetría de orden tres: son líneas que pasan por el centro de una cara y el vértice opuesto. Si giras el tetraedro 120 grados alrededor de estos ejes, se ve igual.
Seis planos de simetría: son superficies planas que dividen el tetraedro en dos mitades idénticas. Cada uno de estos planos pasa por una arista y el punto medio de la arista opuesta.
Tres ejes de simetría de orden dos: son líneas que pasan por los puntos medios de dos aristas opuestas. Si giras el tetraedro 180 grados alrededor de estos ejes, se ve igual.

Todas estas simetrías le dan al tetraedro un "orden de simetría" total de 24.

Autoconjugación

El tetraedro regular es el único sólido platónico que es "autoconjugado". Esto significa que si construyes el poliedro dual de un tetraedro, el resultado es otro tetraedro.

Proyecciones

Cuando proyectas un tetraedro regular sobre un plano (como su sombra), las formas que puedes ver son:

Triángulos: Si lo miras directamente desde una cara, verás un triángulo equilátero.
Cuadriláteros: Si lo miras desde un ángulo diferente, puedes ver un cuadrado. Esto ocurre si el plano de proyección es paralelo a dos aristas opuestas.

Secciones

Si cortas un tetraedro regular con un plano, las formas que puedes obtener son:

Triángulos: Si el corte es paralelo a una de sus caras, la sección será un triángulo equilátero.
Cuadriláteros: Si el corte es paralelo a dos aristas opuestas, la sección será un rectángulo. Si el corte está justo a la mitad entre esas aristas, la sección será un cuadrado.

Combinaciones con Otros Sólidos

Puedes meter un tetraedro regular dentro de un cubo. Los vértices del tetraedro coincidirán con algunos vértices del cubo.
Si combinas dos tetraedros regulares dentro de un cubo, sus aristas serán perpendiculares.
La figura que se forma al unir dos tetraedros de esta manera se llama estrella octángula de Kepler.
La parte que tienen en común estos dos tetraedros es un octaedro regular.

No es posible llenar todo el espacio solo con tetraedros regulares.

Tetraedros en la Naturaleza y la Tecnología

Estructura tetraédrica del metano.

La forma tetraédrica aparece en muchos lugares:

Moléculas: En la naturaleza, algunas moléculas tienen forma de tetraedro. Un ejemplo es la molécula de metano (CH₄). El átomo de carbono está en el centro y los cuatro átomos de hidrógeno están en los vértices de un tetraedro.
Cristales: Algunas estructuras cristalinas naturales también tienen forma tetraédrica.

Aunque es una forma simple, no hay muchos objetos cotidianos con forma de tetraedro.

Envases: La empresa sueca Tetra Pak creó envases de cartón con forma tetraédrica en los años 50. Eran fáciles de fabricar.
Señalización de carreteras: Se usan elementos de balizamiento de carreteras con forma de tetraedro. Como siempre tienen un vértice hacia arriba, son fáciles de colocar y no se caen fácilmente.
Anclas y escolleras: La forma tetraédrica es buena para engancharse. Por eso se usa en anclas de barco o en bloques de hormigón para proteger las costas, como los tetrápodos y los doloses.

Tetrápodos para escollera.

Dolos para escollera.

Cometas: A principios del siglo XX, Alexander Graham Bell (el inventor del teléfono) experimentó con cometas tetraédricas. Estas cometas estaban hechas de muchas celdas con forma de tetraedro.
Sondas espaciales: La sonda espacial Mars Pathfinder de la NASA tenía forma de tetraedro. Sus caras se abrieron como pétalos cuando aterrizó en Marte en 1997.
Dados: Los dados de cuatro caras, usados en juegos de rol, tienen forma de tetraedro. Como no tienen una cara hacia arriba, el valor se marca en los vértices o en la base.

Dado para juego de rol.

Poliedros Relacionados

Pirámides
Digonal	Triangular	Cuadrada	Pentagonal	Hexagonal	Heptagonal	Octogonal	Eneagonal	Decagonal...
Impropia	Regular	Equilátera		Isósceles

Ver También

Tetraedro de Reuleaux
Tetraedro trirrectangular
Anexo:Ecuaciones de figuras geométricas

Véase también

En inglés: Tetrahedron Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Tetraedro&oldid=5009512»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Tetraedro para Niños. Enciclopedia Kiddle.