Teseracto para niños
| Teseracto | |
|---|---|
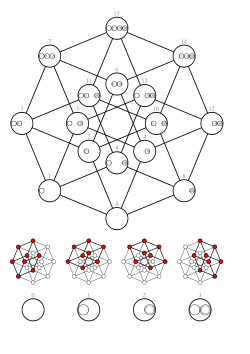
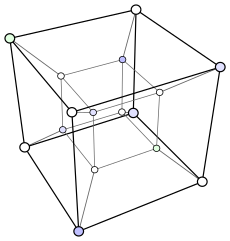 Diagrama de Schlegel |
|
| Tipo | Politopo regular |
| Familia | Hipercubo |
| Celdas | 8 {4,3} |
| Caras | 24 {4} |
| Aristas | 32 |
| Vértices | 16 |
| Símbolo de Schläfli | {4,3,3} {4,3}x{} {4}x{4} {4}x{}x{} {}x{}x{}x{} |
| Diagrama de Coxeter-Dynkin | |
| Grupo de simetría | B4, [3,3,4] |
| Dual | 16-celdas |
| Figura de vértice | (3.3.3) |
| Propiedades | Convexo, isogonal, isotoxal, isoedral |
En geometría, el teseracto es como un cubo pero en cuatro dimensiones. Imagina que un cuadrado es a un cubo lo que un cubo es a un teseracto. Así como un cubo tiene seis caras cuadradas, un teseracto tiene ocho "celdas" cúbicas. Es una de las seis formas geométricas regulares que existen en cuatro dimensiones.
También se le conoce como ocho celda, 8-celda, C8, octácoro, octaedroide, prisma cúbico o tetracubo. Es el hipercubo de cuatro dimensiones, parte de la familia de los hipercubos.
Un teseracto está formado por ocho cubos tridimensionales. Estos cubos se organizan en un espacio que tiene una cuarta dimensión. Piensa en la longitud, la altura y la profundidad como las primeras tres dimensiones. La cuarta dimensión sería algo diferente, que no podemos ver directamente. En este espacio de cuatro dimensiones, el teseracto es como un cubo de cuatro lados. Tiene 16 vértices, 32 aristas, 24 caras cuadradas y 8 celdas cúbicas.
Contenido
¿De dónde viene la palabra "teseracto"?
La palabra "teseracto" fue creada y usada por primera vez en 1888 por Charles Howard Hinton. Apareció en su libro A New Era of Thought. La palabra viene del griego antiguo téssereis aktines, que significa "cuatro rayos". Esto se refiere a las cuatro aristas que salen de cada vértice del teseracto.
¿Cómo podemos entender un teseracto?
Es muy difícil imaginar un teseracto porque solo podemos ver en tres dimensiones. Piensa en un teseracto como un cubo que se mueve a través de una cuarta dimensión, dejando un rastro de todas sus posiciones.
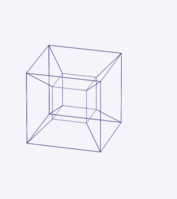
Como los humanos solo podemos ver en tres dimensiones, no podemos ver un teseracto completo. Solo podemos ver sus "proyecciones". Una proyección es como la sombra de un objeto. Cuando un cubo se proyecta en una superficie plana (dos dimensiones), se ve como un cuadrado. De manera similar, cuando un teseracto se proyecta en nuestro espacio tridimensional, se ve como dos cubos, uno dentro del otro, con sus esquinas conectadas.
Sin embargo, en un teseracto real de cuatro dimensiones, todas sus aristas tendrían la misma longitud y todos sus ángulos serían de 90 grados.
Propiedades del teseracto
¿Qué es un teseracto unitario?
Un cubo unitario de cuatro dimensiones es un conjunto de puntos en un espacio de cuatro dimensiones. Estos puntos tienen coordenadas (x, y, z, t) donde cada coordenada está entre 0 y 1.
¿Cuántos vértices tiene?
Los vértices de un teseracto unitario son los puntos donde cada coordenada es 0 o 1. Hay 16 de estos vértices.
¿Cuántas aristas tiene?
Las aristas son las líneas que conectan los vértices. En un teseracto, cada arista es un segmento donde solo una de las cuatro coordenadas cambia, mientras las otras tres se mantienen fijas en 0 o 1. Un teseracto tiene 32 aristas.
¿Cuántas caras y celdas tiene?
Las caras bidimensionales (cuadrados) se forman uniendo dos aristas. Las celdas tridimensionales (cubos) se forman uniendo tres aristas. Un teseracto tiene 24 caras cuadradas y 8 celdas cúbicas.
¿Cómo se calcula el número de elementos?
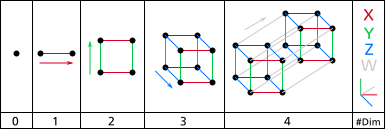
Podemos entender cómo se forma un teseracto paso a paso:
- Paso 0: Empezamos con 1 vértice.
- Paso 1: Si movemos el vértice, creamos otro vértice y 1 arista. Ahora tenemos 2 vértices y 1 arista.
- Paso 2: Si movemos la arista de forma perpendicular, duplicamos los vértices. Se crean 4 aristas y 1 cara (un cuadrado). Ahora tenemos 4 vértices, 4 aristas y 1 cara.
- Paso 3: Si movemos la cara de forma perpendicular, duplicamos los vértices de nuevo. Se crean 12 aristas, 6 caras y 1 volumen (un cubo). Ahora tenemos 8 vértices, 12 aristas, 6 caras y 1 cubo.
- Paso 4: Si movemos el cubo de forma perpendicular en la cuarta dimensión, duplicamos los vértices otra vez. Se crean 32 aristas, 24 caras, 8 cubos y 1 teseracto. ¡Así llegamos a 16 vértices, 32 aristas, 24 caras, 8 volúmenes y 1 hipervolumen (el teseracto)!
Representaciones del teseracto

Una animación de la transformación de dimensiones descrita
|
Podemos proyectar un teseracto en espacios de tres o dos dimensiones, de la misma forma que proyectamos un cubo en una superficie plana.
Una forma de entenderlo es que un teseracto se forma uniendo dos cubos. Es como cuando unes dos cuadrados para formar un cubo: pones dos copias del objeto de menor dimensión y conectas sus vértices. Todas las aristas de un teseracto tienen la misma longitud.
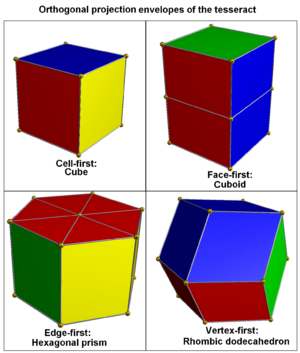
Proyecciones en 3 dimensiones
|
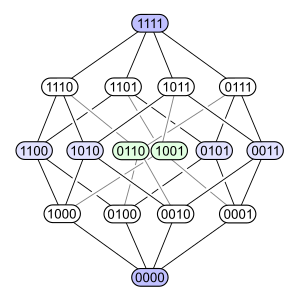
Cuando proyectamos un teseracto en el espacio tridimensional, puede verse de diferentes maneras, dependiendo de cómo lo "miremos" desde la cuarta dimensión. Por ejemplo, si lo proyectamos de una manera específica, las celdas más cercanas y más lejanas se ven como un cubo, y las otras seis celdas se ven como las caras de ese cubo. |
¿Cómo se puede "desplegar" un teseracto?
Desarrollo 3-D de un teseracto
Así como un cubo se puede "desplegar" en seis cuadrados planos (como una caja de cartón desarmada), un teseracto se puede desplegar en ocho cubos en el espacio tridimensional. A esto se le llama una "red" de un politopo. Existen 261 formas diferentes de desplegar un teseracto.
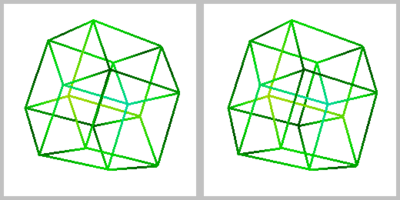 Proyección estereoscópica 3D de un teseracto (vista paralela) |
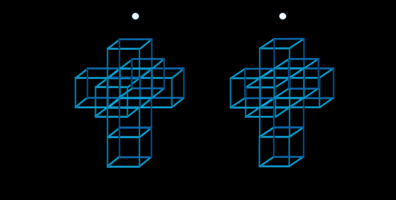 Vista estereográfica del desarrollo 3D de un hipercubo. Se debe observar con los ojos cruzados (no requiere gafas especiales) |
El teseracto en la cultura popular
Desde que se descubrieron, los hipercubos de cuatro dimensiones han aparecido en el arte, la arquitectura y la ciencia ficción. Aquí tienes algunos ejemplos:
- "And He Built a Crooked House": Una historia de ciencia ficción de 1940 de Robert A. Heinlein que trata sobre un edificio con forma de hipercubo de cuatro dimensiones.
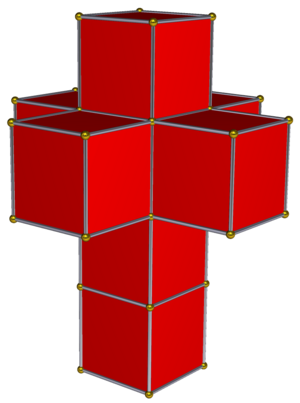
- La Crucifixión: Una famosa pintura de 1954 de Salvador Dalí que muestra un hipercubo de cuatro dimensiones desplegado en forma de cruz.
- El Arco de La Défense: Un gran monumento y edificio cerca de París, Francia, terminado en 1989. Su ingeniero, Erik Reitzel, dijo que el Grande Arche fue diseñado para parecerse a la proyección de un hipercubo.
- Fez: Un videojuego donde el personaje principal puede ver más allá de las dos dimensiones que otros personajes ven. Usa esta habilidad para resolver acertijos. En el juego aparece un teseracto llamado "Dot" que ayuda a navegar y a usar habilidades, lo que encaja con la idea de ver más allá de lo que normalmente percibimos.
- Cube 2: Hypercube: Una película canadiense de 2002 donde los personajes están atrapados dentro de un teseracto lleno de trampas y deben escapar.
La palabra "teseracto" también se ha usado en muchas otras obras de ciencia ficción, a veces sin mucha relación con la forma geométrica de cuatro dimensiones.
Véase también
 En inglés: Tesseract Facts for Kids
En inglés: Tesseract Facts for Kids