Aritmética para niños
La aritmética es una parte muy importante de las matemáticas. Se encarga de estudiar los números y las operaciones básicas que hacemos con ellos: adición (sumar), sustracción (restar), multiplicación y división.
La palabra "aritmética" viene del griego "arithmetikós", que significa "relacionado con los números". Desde hace mucho tiempo, la aritmética ha evolucionado. Al principio, en la Antigua Grecia, se enfocaba en entender las propiedades de los números. Hoy en día, la "Aritmética Elemental" es lo que aprendemos en la escuela. También se refiere a la "alta aritmética", que es un estudio más profundo de los números, conocido como Teoría de Números.
Contenido
Operaciones aritméticas básicas
Las cuatro operaciones principales de la aritmética son:
- Sumar (adición)
- Restar (sustracción)
- Multiplicar
- Dividir
Cuando empiezas a aprender matemáticas en la escuela, lo que haces es aritmética. La diferencia con el Álgebra es que en álgebra usamos letras para representar números desconocidos. La aritmética también nos ayuda a entender conceptos como las potencias (números multiplicados por sí mismos varias veces) y las raíces (encontrar un número que, multiplicado por sí mismo, dé el original).
Además de las operaciones básicas, la aritmética nos ha dado herramientas como las fracciones y los porcentajes. Las fracciones nos permiten trabajar con partes de un todo, y los porcentajes nos ayudan a entender proporciones. Estas herramientas son muy útiles en la vida diaria, en la ciencia y en muchas otras áreas.
¿Qué instrumentos se usaron para calcular?
Desde hace miles de años, las personas han usado diferentes objetos para contar y hacer cálculos. Al principio, usaban sus dedos o palos con marcas.
Historia de la aritmética
¿Cómo empezó la aritmética?
La aritmética es tan antigua como las matemáticas. Los primeros registros de conteo se encuentran en huesos y palos tallados de la Edad de Piedra. Estos se usaban para llevar la cuenta de cosas o para calendarios.
Aritmética en civilizaciones antiguas
Los babilonios, hace unos 3800 años, ya sabían mucho de aritmética. Usaban tablillas de barro con escritura cuneiforme para resolver problemas. Los egipcios también hacían cálculos avanzados con un sistema de fracciones. Sus papiros muestran sumas, restas, multiplicaciones y divisiones.
En la Antigua Grecia, la aritmética se veía como el estudio de las propiedades de los números, no tanto como una herramienta para hacer cálculos. Los griegos diferenciaban entre "número" (que para ellos eran los números naturales) y "magnitud" (como las medidas geométricas). Euclides, en sus famosos libros Los elementos, dedicó varios a la aritmética.
Nicómaco de Gerasa, un filósofo griego, fue el primero en diferenciar claramente la aritmética de otras ciencias como la música o la astronomía. Él le dio a la aritmética un significado más parecido al que conocemos hoy, enfocado en los números enteros y sus propiedades.
Diofanto de Alejandría escribió Arithmetica, donde por primera vez se reconocieron las fracciones como números y se usaron símbolos para representar cantidades desconocidas. Sus trabajos llevaron a grandes avances en la teoría de números.
La aritmética en la Edad Media y el Renacimiento
Después de los griegos, los avances matemáticos continuaron en las regiones islámicas. Los matemáticos árabes tradujeron y conservaron muchas obras griegas. En el siglo XI, matemáticos como Fibonacci llevaron estos conocimientos de vuelta a Europa.
En 1202, Fibonacci publicó su libro Liber Abaci, donde introdujo el sistema de numeración decimal con los números arábigos (los que usamos hoy: 0, 1, 2, 3...). Antes, se usaban los números romanos, que hacían los cálculos muy difíciles. Gracias a Fibonacci, las nuevas técnicas aritméticas se hicieron muy populares en Europa.
Aritmética en América antes de Colón
Los mayas usaban un sistema de numeración basado en el número 20 y fueron de las primeras civilizaciones en desarrollar el concepto del cero. Lo usaban para medir el tiempo y el comercio.
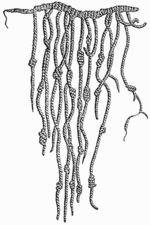
Los incas eran muy buenos en cálculos para la economía y el comercio. Usaban los quipus (cuerdas con nudos) y las yupanas (tableros de cálculo). Su aritmética era sencilla pero muy efectiva para la contabilidad, basada en un sistema decimal. También conocían el cero y dominaban la suma, resta, multiplicación y división.
La aritmética en China
La matemática china se desarrolló de forma independiente. Uno de los textos más antiguos es Zhou Bi Suan Jing, del año 300 a.C. Los chinos usaban un sistema decimal posicional con numeración con varillas mucho antes que otros. Esto les permitía representar números muy grandes y hacer cálculos con el suanpan (o ábaco chino).
El cero y la notación posicional en la India
La matemática hindú hizo un invento muy importante: la notación posicional y el uso del cero como un valor nulo. Esto ocurrió entre los siglos I y VIII. A diferencia de los egipcios, griegos y romanos, que también usaban un sistema decimal pero sin el cero y sin valor posicional, los hindúes crearon un sistema mucho más eficiente.
Este sistema fue transmitido a Occidente por los árabes. Gracias a la introducción de los números árabes y la notación decimal posicional, se pudieron desarrollar los algoritmos de cálculo modernos que usamos hoy.
La aritmética árabe
Los árabes tomaron los conocimientos matemáticos de la India y de Grecia. En la Casa de la sabiduría en Bagdad, tradujeron obras de grandes matemáticos. Al-Juarismi fue clave en el desarrollo del álgebra, que separó los cálculos de la geometría y permitió trabajar con números de una forma nueva.
En el siglo X, se usaban tres sistemas aritméticos: el conteo con los dedos para el comercio, el sexagesimal (de los babilonios) para la astronomía, y el sistema de números indios con valor posicional decimal, que fue el más importante.
Aritmética avanzada
El término "aritmética" también se usa para referirse a la teoría de números. Esta rama de las matemáticas estudia las propiedades de los números enteros, como los números primos, la divisibilidad y las soluciones de ecuaciones con números enteros.
- La aritmética modular estudia los restos de las divisiones.
- La aritmética binaria es la base de las computadoras, usando solo los números 0 y 1.
- La aritmética de Peano es un conjunto de reglas básicas para construir los números naturales.
El Teorema Fundamental de la Aritmética
Este teorema dice que cualquier número entero positivo (mayor que cero) se puede escribir de una única manera como una multiplicación de factores primos. Por ejemplo, el número 12 se puede escribir como 2 x 2 x 3. Este resultado fue descubierto por Euclides y demostrado formalmente por Carl Friedrich Gauss en 1801.
Los teoremas de incompletitud de Gödel
En 1931, Kurt Gödel demostró dos teoremas muy importantes. Uno de ellos dice que, en cualquier sistema matemático formal que sea lo suficientemente complejo como para describir la aritmética, siempre habrá afirmaciones verdaderas que no se pueden demostrar dentro de ese mismo sistema. Esto significa que las matemáticas son muy profundas y siempre habrá cosas por descubrir.
Libros importantes sobre aritmética
-
Papiro de Ahmes; de hace unos 3800 a 4000 años.
-
Las nueve lecciones del arte matemático; de la Dinastía Zhou en China.
-
Elementos de Euclides, alrededor del 300 a.C. Edición de 1570.
-
Arithmetica de Diofanto (alrededor del 280 d.C.). Edición de 1621.
-
Hisāb al-ŷabr wa'l muqābala, de al-Juarismi, siglo IX.
-
Disquisitiones arithmeticae de Carl Friedrich Gauss (1798). Publicado en 1801.
Más sobre aritmética
Véase también
 En inglés: Arithmetic Facts for Kids
En inglés: Arithmetic Facts for Kids