Regla de cálculo para niños
La regla de cálculo es una herramienta antigua que se usaba para hacer cálculos matemáticos. Funciona como una especie de computadora mecánica. Tiene varias escalas con números que se mueven, lo que ayuda a hacer operaciones complicadas como multiplicaciones y divisiones de forma rápida.
Estas reglas se adaptaron para diferentes áreas, como la ingeniería, la construcción o las finanzas. La mayoría medían unos 25 centímetros, lo que permitía una buena precisión. También había versiones más pequeñas, de bolsillo, de unos 10 centímetros.
La regla de cálculo fue muy popular desde mediados del siglo XIX hasta la década de 1970. En esa época, casi todos los ingenieros tenían una. Al principio, se hacían de madera, latón o hueso, y luego de plástico. Su uso disminuyó mucho cuando aparecieron las calculadoras electrónicas y las computadoras personales. Hoy en día, se ven principalmente en museos o se usan para enseñar matemáticas básicas.
Contenido
Historia de la Regla de Cálculo
Desde antes del siglo XVI, ya existían herramientas con escalas para ayudar en los cálculos. Por ejemplo, el famoso científico Galileo Galilei describió un instrumento para calcular fórmulas de trigonometría. Algunos de estos primeros sistemas venían de antiguos astrolabios o herramientas de navegación.
¿Quién inventó la regla de cálculo?
No hay un acuerdo total sobre quién la inventó. Algunos historiadores creen que fue el matemático Edmund Wingate a mediados del siglo XVI. Otros dicen que fue el reverendo William Oughtred en 1636.
El desarrollo de la regla de cálculo avanzó mucho gracias a los logaritmos, que John Napier publicó en 1614. Años después, el astrónomo Edmund Gunter aplicó la idea de los logaritmos a las escalas de cálculo. Creó la "escala de Gunter", que servía para cálculos de navegación.
William Oughtred tomó la idea de Gunter y creó dos escalas que se deslizaban una sobre otra. Al alinear los números, se podían hacer cálculos. Así nació la primera regla de cálculo tal como la conocemos. A finales del siglo XVII, ya se usaban diferentes versiones de estas reglas.
Mejoras y evolución en el diseño
En 1675, Sir Isaac Newton usó tres escalas logarítmicas paralelas para resolver ecuaciones. Él fue el primero en sugerir usar un cursor, una pieza que se desliza y ayuda a leer los resultados.
Más tarde, Henry Coggeshall diseñó la "regla de carpintero" en 1682, para medir madera. En 1683, el experto en medidas Thomas Everard creó un instrumento con escalas para calcular impuestos sobre barriles de cerveza y vino.
Durante el siglo XVIII, las reglas de cálculo se modificaron para ser más precisas. Ingenieros como James Boulton y James Watt mejoraron los diseños. En 1815, el físico Peter Mark Roget inventó las escalas log-log, que permitían calcular cualquier raíz cuadrada.
En 1831, Victor Amadee Mannheim propuso un sistema para estandarizar las escalas, llamado "sistema Mannheim". Este sistema incluía una regleta deslizante que hacía los cálculos más cómodos.
A finales del siglo XIX, muchas empresas empezaron a fabricar reglas de cálculo debido a la gran demanda. La Revolución Industrial necesitaba más cálculos para las nuevas máquinas. En Estados Unidos, marcas como Keuffel & Esser, Dietzgen y Post Company fueron líderes.
El sistema Rietz y su impacto
La evolución de las reglas de cálculo continuó durante la Revolución Industrial. En la década de 1870, empresas alemanas como Dennert and Pape (fabricantes de Aristo) y Faber (más tarde Faber-Castell) eran importantes.
En 1902, Max Rietz unificó los sistemas de escalas con el "sistema Rietz" (también llamado Mannheim). Esto significó que un ingeniero que aprendiera este sistema podía usar cualquier regla de cálculo que lo implementara, lo que facilitó mucho su uso y comparación. Este sistema fue muy aceptado hasta que Alwin Walter propuso nuevos cambios en 1934, creando el "Sistema Darmstadt".
El fin de una era: la llegada de las calculadoras
La época dorada de la regla de cálculo duró más de un siglo, desde mediados del siglo XIX hasta la década de 1970. Era la herramienta de cálculo más usada en ciencia e ingeniería antes de que aparecieran las calculadoras de bolsillo.
A mediados del siglo XX, se dejó de usar madera para fabricarlas y se empezó a usar plástico. En 1930, Philip Dalton inventó una regla de cálculo circular llamada E6B, que se usaba para cálculos aeronáuticos durante el vuelo. Fue muy útil en la Segunda Guerra Mundial.
El uso de las reglas de cálculo siguió creciendo en los años 50 y 60, incluso cuando las computadoras digitales empezaban a aparecer. Sin embargo, su popularidad cayó rápidamente con la llegada de las calculadoras electrónicas. El lanzamiento del modelo HP-35 de Hewlett-Packard el 1 de febrero de 1972 marcó el principio del fin para las reglas de cálculo.
Para 1980, la producción de reglas de cálculo casi había desaparecido. Hoy en día, solo se fabrican en pequeñas cantidades para usos muy específicos, como en la navegación, o para coleccionistas.
Partes de una Regla de Cálculo
Una regla de cálculo tiene varias partes principales:
- Soporte básico o cuerpo: Es la parte principal, generalmente rectangular. Tiene una ranura en el centro.
- Corredera: Es una pieza más pequeña que se desliza por la ranura central del cuerpo.
- Escalas: Son las líneas y números grabados en las caras de estas piezas. Algunas reglas tienen escalas en la parte trasera, y se les llama "dúplex". Las "simplex" solo tienen escalas en la parte frontal.
- Cursor: Es una pieza transparente y móvil con una línea fina, llamada "hilo" o "índice". Ayuda a alinear y leer los números en las escalas, especialmente cuando están separadas. Algunos cursores tenían una lupa para ver mejor.
¿Qué tan precisas eran?
La precisión de una regla de cálculo dependía de la longitud de sus escalas. Cuanto más largas eran las escalas, más precisos eran los resultados. Sin embargo, la precisión también dependía de la persona que la usaba, ya que a menudo había que "estimar" los valores entre las marcas.
Las reglas de cálculo comunes solían dar resultados con hasta tres cifras significativas. Esto significa que los últimos números eran a menudo una estimación. Aunque esto pueda parecer una limitación, en muchas aplicaciones prácticas era suficiente, ya que los datos de partida tampoco solían ser más precisos. Esto evitaba la "falsa precisión" que a veces pueden dar las calculadoras electrónicas.
Materiales y formas
A lo largo de la historia, las reglas de cálculo se hicieron de muchos materiales, como cartón, madera (boj, bambú), metales (bronce, latón) y plásticos.
La forma más común era la rectangular, de ahí su nombre de "regla". Sin embargo, también existieron otros diseños.
El círculo de cálculo
También conocido como "regla de cálculo circular", fue inventado desde los inicios. Es más compacto que la regla rectangular para la misma longitud de escalas. Además, los resultados de las operaciones nunca se "salen" de la escala, ya que es un círculo cerrado. Sin embargo, puede ser un poco menos intuitivo de usar.
Se fabricaron en dos estilos principales: con dos círculos concéntricos y un cursor, o con un disco fijo y dos cursores móviles. También hubo modelos que parecían relojes de bolsillo o de pulsera.
Reglas de cálculo cilíndricas
Un ejemplo famoso es la Otis King, diseñada por Otis Carter Formby King. Tenía una escala en espiral grabada en un cilindro. Se usó inicialmente para cálculos específicos en tiendas y se fabricó desde 1922 hasta 1972.
¿Cómo se usa una regla de cálculo?
Para usar bien una regla de cálculo, es clave entender cómo funcionan sus escalas. Las escalas básicas son bastante sencillas, especialmente si tienen símbolos que las identifican.
Si no se sabe qué significan las escalas, lo mejor es consultar el manual del modelo específico. Hoy en día, se puede encontrar mucha información en internet.
Las otras dos habilidades importantes son: practicar la lectura de los valores y saber dónde colocar el punto decimal.
Las escalas de las reglas de cálculo suelen estar muy llenas de números, lo que puede confundir al leer los valores o los resultados. Para evitar errores, hay que prestar mucha atención y practicar.
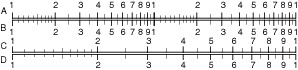
Las escalas logarítmicas solo muestran la parte decimal de los números. Por eso, la escala se repite cada diez números, en lo que se llama un "ciclo". Las escalas C y D, que son las básicas, van del 1 al 10. Las escalas A y B son de dos ciclos y muestran los cuadrados de los números de las escalas C y D.
Es importante no confundir los números. Por ejemplo, si calculas 1.5 al cuadrado, el resultado es 2.25. Pero si calculas 4.2 al cuadrado, el resultado no puede ser 1.76, sino 17.6. Siempre es útil hacer una estimación mental para asegurarse de que el resultado tiene sentido.
Si necesitas hacer varias operaciones seguidas, es buena idea anotar los resultados intermedios en un papel. Con práctica, también puedes usar el cursor para transferir resultados.
Una ventaja de estas reglas es que si pueden hacer una operación, también pueden hacer la inversa. Por ejemplo, si sirven para multiplicar, también sirven para dividir. Solo hay que cambiar el orden de las escalas.
Tipos de Escalas y Modelos
Durante los primeros dos siglos, las reglas de cálculo eran hechas a mano y en pocas cantidades. Las funciones que ofrecían dependían del inventor o del cliente. Al principio, se usaban maderas finas como la caoba, o materiales como el hueso y el latón.
A medida que avanzaba el siglo XIX y crecían los conocimientos científicos y la industria, más ingenieros necesitaban hacer cálculos. Esto creó un mercado para las reglas de cálculo, y surgieron modelos con un número y tipo de escalas más estables.
Modelos de escalas principales
El primer modelo realmente popular fue diseñado por el artillero francés Amédée Mannheim en 1850. Parte de su éxito se debió a que incluyó el cursor, que la mayoría de las reglas anteriores no tenían. Este modelo fue adoptado por el ejército francés y se empezó a fabricar en masa a partir de 1859.
Las escalas suelen identificarse con una letra grabada en su extremo izquierdo. Aunque no es totalmente uniforme, la mayoría de los fabricantes usan una terminología similar.
Los tres tipos básicos de reglas de cálculo, según sus escalas, son:
- Mannheim: Incluye las escalas A, B, C, D.
- Rietz: Añade las escalas K, L, S, T, ST, CI a las del modelo Mannheim (propuesta por Max Rietz en 1902).
- Darmstadt: Añade principalmente las escalas LL al modelo Rietz (propuesta por Alwin Walther en 1934).
Escalas comunes y sus funciones
|
|
|
|
|
|
Escala para calcular cuadrados; tiene dos ciclos logarítmicos. |
|
|
|
Escala para calcular cuadrados; similar a la A, pero en la regleta móvil. |
|
|
|
Duplicado de la escala básica; tiene un ciclo logarítmico. |
|
|
|
Escala básica; tiene un ciclo logarítmico. |
|
|
|
Escala para calcular cubos; tiene tres ciclos logarítmicos. |
|
|
|
Escala C "invertida", se lee de derecha a izquierda; para calcular recíprocos. |
|
|
|
Escala C "desplazada"; su inicio es un valor fijo, como el número pi. |
|
|
|
Escala para ángulos de senos (se usa con la escala A). |
|
|
|
Escala para ángulos de tangentes (se usa con la escala A). |
|
|
|
Escala para senos y tangentes de ángulos pequeños; para convertir grados a radianes. |
|
|
|
Escala lineal para obtener la parte decimal de los logaritmos comunes (base 10). |
|
|
|
Escala lineal para obtener los logaritmos naturales (base e). |
|
|
|
Conjunto de escalas doblemente logarítmicas (log-log), para operaciones con exponentes. |
|
Las reglas especializadas pueden tener otras escalas para cálculos específicos, como los de estadística o ingeniería eléctrica.
|
||
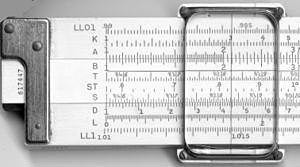
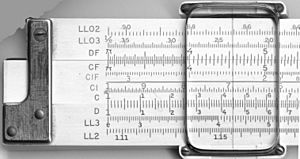
| Escalas de las caras anterior y posterior de una regla dúplex K&E 4081-3. |
¿Cómo funciona matemáticamente?
Las operaciones que se pueden hacer con una regla de cálculo se dividen en dos grupos.
Nomogramas estáticos
En el primer grupo, las escalas están fijas, como en un nomograma. Solo se mueve el cursor para obtener los resultados. Por ejemplo, para elevar un número al cuadrado o sacar su raíz cuadrada, no necesitas mover la regleta central, a veces ni siquiera el cursor. Estas operaciones se representan con ecuaciones de dos variables, como y = f(x), donde la función puede ser elevar a una potencia o calcular un logaritmo.
Escalas móviles
Las operaciones del segundo grupo requieren mover la regleta central. Esto es lo que se llama "instrumentos nomo-mecánicos", que usan un mecanismo simple para ayudar a los cálculos.
Estas operaciones son principalmente la suma y la multiplicación (y sus inversas, la resta y la división). En estos casos, lo que se hace es sumar o restar segmentos de las escalas.
Suma de segmentos
Aunque se dice que la regla de cálculo no sirve para sumar, en realidad sí lo hace, pero de una manera especial. Si deslizas dos reglas normales una sobre otra, y pones el inicio de la de arriba frente al número 3 de la de abajo, verás que cada número de la regla de arriba se alinea con otro de la de abajo que es la suma de ese número más 3.
La razón por la que las reglas de cálculo normales no tienen escalas para sumar es doble: primero, la suma es una operación que la mayoría de la gente puede hacer mentalmente; y segundo, si incluyeran escalas para sumar, la regla sería demasiado larga para ser útil. Por ejemplo, una regla de 25 cm solo podría sumar hasta "16+9".
Multiplicación
El "truco" de la regla de cálculo es que, aunque hace sumas de segmentos, las escalas están calibradas de una manera especial para que esas sumas se conviertan en multiplicaciones.
Imagina una regla normal graduada en centímetros. Ahora, debajo de ella, colocamos otra línea con los valores de los logaritmos decimales de los números de la primera escala. El punto 0 de ambas escalas coincide.
Esto fue lo que hizo Edmund Gunter en 1620. Él inscribió una escala similar en un instrumento de más de medio metro de largo. Los cálculos se hacían usando compases, lo cual era común en esa época.
Si ahora repetimos el proceso de sumar segmentos usando dos de estas escalas logarítmicas, el resultado es muy diferente.
Si la escala superior se mueve 1.5 unidades sobre la inferior, el número que aparece debajo de cada marca superior no es la suma de ese número más 1.5, sino ese número multiplicado por 1.5. Esto sucede gracias a una propiedad de los logaritmos: log a + log b = log (a x b). La regla de cálculo "esconde" los logaritmos y nos muestra directamente el resultado de la multiplicación.
Ver también
- Computador analógico
- Nonio
- Nomograma
- Volvelle
- Regla de cálculo Coggeshall
- E6B Flight Computer
Véase también
 En inglés: Slide rule Facts for Kids
En inglés: Slide rule Facts for Kids