Coma flotante para niños

Enciclopedia para niños

La representación de coma flotante (en inglés, floating point) es una forma especial de notación científica que usan las computadoras. Permite representar números reales muy grandes o muy pequeños de forma eficiente y compacta. También facilita que las computadoras realicen cálculos con estos números. El estándar más común para esto es el IEEE 754.

¿Qué es la Notación Científica?

La representación de coma flotante es muy parecida a la notación científica que ya conoces, pero con algunas diferencias. Para entenderla bien, primero vamos a repasar la notación científica.

Cómo se Representa un Número

La notación científica se usa para escribir números reales. Un número real (que llamaremos r) se representa con tres partes:

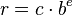
$r=c \cdot b^e \,\!$

c. El coeficiente: Es un número con un solo dígito antes de la coma y varios dígitos después.
b. La base: En nuestro sistema decimal, la base es 10. En el sistema binario de las computadoras, la base es 2.
e. El exponente: Es un número entero que indica a qué potencia se eleva la base.

El Coeficiente

El coeficiente tiene un signo que nos dice si el número real es positivo o negativo.

También tiene una cantidad específica de dígitos importantes. Estos dígitos nos indican qué tan preciso es el número. Cuantos más dígitos tenga el coeficiente, más precisa será la representación. Por ejemplo, el número π se puede escribir como 3,14 x 10⁰ (con 3 dígitos importantes) o como 3,14159265359 x 10⁰ (con 12 dígitos importantes). La segunda forma es mucho más precisa.

La Base y el Exponente

El coeficiente se multiplica por la base elevada a una potencia (el exponente). En el sistema decimal, la base es 10. Cuando multiplicamos el coeficiente por la base elevada a una potencia, la coma del coeficiente se mueve. Se desplaza tantas posiciones como indique el exponente.

Si el exponente es positivo, la coma se mueve hacia la derecha.
Si el exponente es negativo, la coma se mueve hacia la izquierda.

Veamos cómo cambia un número al variar el exponente:

2,71828 x 10^-2 es 0,0271828
2,71828 x 10^-1 es 0,271828
2,71828 x 10 ⁰ es 2,71828 (el exponente cero significa que la coma no se mueve)
2,71828 x 10 ¹ es 27,1828
2,71828 x 10 ² es 271,828

Un Ejemplo Práctico

Aquí tienes un ejemplo de un número en notación científica:

-1,234 567 89 x 10³

El coeficiente es -1,23456789. Tiene 9 dígitos importantes y se multiplica por 10 elevado a la 3. El signo del coeficiente nos dice que el número real es negativo.

El valor del exponente nos indica cuántas posiciones debe moverse la coma del coeficiente. El signo del exponente nos dice si el movimiento es hacia la derecha (exponente positivo) o hacia la izquierda (exponente negativo). Si el exponente es cero, la coma no se mueve. Por eso se llama "coma flotante", porque la coma "flota" o se mueve según el exponente.

En el ejemplo -1,23456789 x 10³, el exponente es 3 positivo. Esto significa que la coma del coeficiente -1,23456789 debe moverse 3 posiciones hacia la derecha. El resultado es el número real:

-1234,567 89

Aquí tienes una tabla con más ejemplos de números reales y cómo se escriben en notación científica con tres dígitos importantes:

Número real	Notación científica
123 000 000 000 000 000 000,0	1,23 x 10²⁰
123 000 000,0	1,23 x 10⁸
1230,0	1,23 x 10³
123,0	1,23 x 10²
12,3	1,23 x 10¹
1,23	1,23 x 10⁰
0,123	1,23 x 10^-1
0,012 3	1,23 x 10^-2
0,001 23	1,23 x 10^-3
0,000 000 012 3	1,23 x 10^-8
0,000 000 000 000 000 000 012 3	1,23 x 10^-20

Como puedes ver, la notación científica hace que los números muy grandes o muy pequeños sean mucho más fáciles de escribir. Por eso se usa mucho en ciencia, donde se manejan cifras enormes (como la masa del Sol) o muy pequeñas (como la carga de un electrón). Y por eso también se usa en las computadoras, en forma de coma flotante.

Cómo lo Usan las Computadoras y Calculadoras

Las computadoras y calculadoras pueden mostrar los números en notación científica de diferentes maneras. Por ejemplo, la velocidad de la luz, que es 2,99792458 x 10⁸, puede aparecer así:

Notación	Comentario
2,99792458 x 10⁸	Es la notación científica estándar.
2,99792458e8	Es común en computadoras y calculadoras; a veces la "e" es mayúscula.
2,99792458d8	Se usa en el lenguaje BASIC para números con mucha precisión.
2,99792458 x 10⁸	Se usa en calculadoras. El exponente se ingresa con teclas como 10^x o EXP.

La Coma Flotante en el Sistema Binario

Representación de la coma flotante

Un número real puede tener muchísimos dígitos. La coma flotante solo puede representar una cantidad limitada de ellos. Esto significa que solo se usan los dígitos más importantes del número real. Por lo tanto, un número real a menudo se representa como una aproximación, no con total exactitud. La precisión depende de cuántos dígitos importantes tenga la representación de coma flotante que se esté usando. Los dígitos menos importantes a veces se redondean o se eliminan. Aunque esto puede causar un pequeño error, es muy útil para manejar números muy grandes o muy pequeños.

En la representación binaria de coma flotante, el primer bit (el de más a la izquierda) indica el signo: 0 para positivo y 1 para negativo. Luego, hay una serie de bits para el exponente. El resto de los bits forman la parte importante del número.

Generalmente, la parte importante está "normalizada". Esto significa que su primer bit siempre es un 1. Para ahorrar espacio, este 1 no se guarda, se asume que está ahí. Se le llama bit oculto o implícito. Antes de hacer cálculos, este bit oculto se vuelve visible. Hay excepciones, como el número cero, o cuando el número es tan pequeño que el exponente no puede representarlo. En esos casos, los dígitos importantes se representan de una manera especial para no perder la precisión de golpe.

Un Ejemplo Binario

Veamos un ejemplo de notación de coma flotante. Abajo hay tres números en una representación de coma flotante de 16 bits. El bit de la izquierda es el signo, luego hay 6 bits para el exponente, seguidos de 9 bits para la parte importante:

$\begin{matrix} \text{Signo}\\ \overbrace{ 1 } \\ 0 \\ 0 \end{matrix} \quad \begin{matrix} \text{Exponente}\\ \overbrace{ 100011 } \\ 011011 \\ 101001 \end{matrix} \quad \begin{matrix} \text{Parte Significativa}\\ \overbrace{ 011101100 } \\ 111001101 \\ 000000001 \end{matrix} \begin{matrix} \ \\ \quad = \mathrm{0xC6EC} \\ \quad = \mathrm{0x37CD} \\ \ = \mathrm{0x5201} \end{matrix}$

El Bit de Signo

El bit de la izquierda nos dice el signo del número. Un 0 significa que el número es positivo, y un 1 significa que es negativo. En los ejemplos de arriba, el primer número es negativo y los otros dos son positivos.

El Exponente

El exponente indica cuánto debe moverse la coma binaria de la parte importante. En este caso, el exponente usa 6 bits, lo que permite 64 valores diferentes. Es un exponente binario (base 2) que puede ir desde -31 hasta +32. Esto significa que la coma binaria puede moverse hasta 31 dígitos binarios a la izquierda (para números muy cercanos a cero) y hasta 32 dígitos binarios a la derecha (para números muy grandes).

El exponente no se guarda directamente como un número con signo (-31 a +32). En su lugar, se le suma un "desplazamiento" (o bias). Para un exponente de 6 bits (64 valores), el desplazamiento es 31. Así, el rango de -31 a +32 se representa internamente como un número entre 0 y 63. Los números entre 31 y 63 representan exponentes de 0 a 32, y los números entre 0 y 30 representan exponentes de -31 a -1.

-31 0 32 <-- Exponente binario real +-------+-------+-------+-------+ 0 31 63 <-- Representación en coma flotante del exponente de 6 bits (Es el exponente binario más un bit de 31)

La Parte Significativa

La parte importante, en este ejemplo, tiene 10 dígitos binarios importantes. De estos, 9 se guardan de forma visible y 1 es implícito (no se guarda).

Como mencionamos, esta parte importante suele estar normalizada y siempre tiene un 1 como el bit más importante. Para ahorrar espacio y aumentar la precisión, este 1 no se almacena. Por eso se le llama bit oculto o implícito. Sin embargo, antes de hacer cualquier cálculo, este bit implícito debe hacerse visible.

Números Reales Representados

La notación genérica de coma flotante que vimos antes representa los siguientes números reales (en binario). El color rojo indica el bit más importante, que es implícito al guardarse, pero se hace explícito al calcular o mostrar la información:

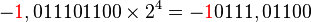-\color{red}1\color{black},011101100 \times 2^{4} = -\color{red}1\color{black}0111,01100

(La coma se mueve 4 posiciones binarias (bits) a la derecha)

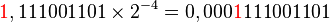\color{red}1\color{black},111001101 \times 2^{-4} = 0,000\color{red}1\color{black}111001101

(La coma se mueve 4 posiciones binarias a la izquierda)

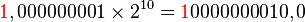\color{red}1\color{black},000000001 \times 2^{10} = \color{red}1\color{black}0000000010,0

(La coma se mueve 10 posiciones binarias a la derecha)

(todos los valores están en representación binaria)

Coma Flotante vs. Coma Fija

Para un mismo tamaño de memoria (bytes), la notación de coma flotante puede ser más lenta de procesar y menos precisa que la notación de coma fija. Esto se debe a que, además de guardar el número, también debe guardar el exponente. Sin embargo, la coma flotante permite representar un rango mucho mayor de números.

Procesadores y Programas Especializados

Las operaciones matemáticas con números de coma flotante son complejas. Por eso, muchos sistemas tienen un procesador especial llamado unidad de coma flotante (FPU) o componentes específicos para estas operaciones. Cuando no hay un hardware así o no puede realizar ciertas operaciones, se usan programas especiales (bibliotecas de software) para hacer los cálculos.

Tipos de Formatos de Coma Flotante

Aquí se muestran algunos formatos binarios de números de coma flotante según el estándar IEEE 754 (2008):

	Representación (número de bits)				Características
Tipo	Signo	Exponente	Significante	Total	Tamaño	Desplazamiento del exponente	Bits de precisión (número de bits importantes)	Dígitos importantes en decimal	Rango
Medio (half)	1	5	10	16	2 bytes (16 bits)	15	11	3,31	-? .. 65504
Simple (single)	1	8	23	32	4 bytes (32 bits)	127	24	7,22	-1,701411733e38 .. 3,402823466e+38
Doble (double)	1	11	52	64	8 bytes (64 bits)	1023	53	15,95	2,2250738585072014e-308 .. 1,7976931348623158e+308
Cuádruple (quad)	1	15	112	128	16 bytes (128 bits)	16383	113	34,02	??

Galería de imágenes

Ver También

Véase también

En inglés: Floating point Facts for Kids

Obtenido de «https://ninos.kiddle.co/index.php?title=Coma_flotante&oldid=4930250»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Coma flotante para Niños. Enciclopedia Kiddle.