Fracción egipcia para niños

Una fracción egipcia es una forma especial de escribir números. Imagina que tienes una fracción, como 3/4. Los antiguos egipcios no la escribían así. En cambio, la representaban como la suma de varias fracciones con un 1 en la parte de arriba (llamadas fracciones unitarias), y donde todos los números de abajo (los denominadores) son diferentes. Por ejemplo, 3/4 se podría escribir como 1/2 + 1/4.

Se ha demostrado que cualquier número positivo que se pueda escribir como fracción (un número racional) puede representarse de esta manera, como una suma de fracciones unitarias distintas.

El ojo de Horus (Udyat) contiene los símbolos jeroglíficos de los primeros números racionales.

¿Qué Son las Fracciones Egipcias?

Las fracciones egipcias son sumas de fracciones donde el numerador (el número de arriba) es siempre 1, y los denominadores (los números de abajo) son números enteros positivos y diferentes entre sí. Por ejemplo, 1/3 + 1/5 es una fracción egipcia, pero 1/3 + 1/3 no lo sería porque los denominadores no son distintos.

Las Matemáticas en el Antiguo Egipto

Los historiadores de las matemáticas nos cuentan que el álgebra, que es una rama de las matemáticas que usa letras y símbolos para resolver problemas, se desarrolló en varias etapas.

El Álgebra de los Antiguos Egipcios

1. Álgebra retórica: En esta etapa, los problemas se explicaban usando solo palabras, como si contaras una historia. 2. Álgebra sincopada: Aquí, algunas palabras se acortaban o se usaban abreviaturas para hacer los problemas más sencillos de escribir y entender. 3. Álgebra simbólica: Esta es la etapa que usamos hoy, donde se usan símbolos como "x" para representar números desconocidos y signos como "+" o "=" para las operaciones.

Los egipcios usaban las dos primeras formas. Sabemos por sus jeroglíficos que los sacerdotes y escribas egipcios usaban palabras como "aha" (que significaba "montón" o "conjunto") para referirse a una cantidad desconocida en sus problemas.

El Papiro de Ahmes: Un Tesoro Matemático

Un ejemplo famoso de esto se encuentra en el Papiro de Ahmes, un documento muy antiguo (de alrededor del año 1650 a.C.) que se guarda en el Museo Británico de Londres. En este papiro, hay un problema que dice:

"Problema 24: Una cantidad y su séptima parte suman 19. ¿Cuál es la cantidad?"

Para resolverlo, los egipcios pensaban de una manera muy práctica. Si la cantidad fuera 7, entonces 7 y su séptima parte (que es 1) sumarían 8. Luego, se preguntaban cuántas veces había que multiplicar 8 para llegar a 19. La misma cantidad de veces que multiplicaran 8, tendrían que multiplicar 7 para encontrar la respuesta.

En nuestras matemáticas modernas, este problema se escribiría como: x + x/7 = 19. La solución es x = 133/8.

Fragmento del Papiro de Ahmes.

¿Cómo Escribían las Fracciones los Egipcios?

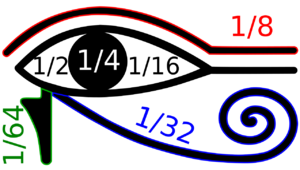
Los antiguos egipcios usaban principalmente fracciones unitarias, como 1/2, 1/3, 1/4, 1/10, etc.

Para escribir una fracción, usaban un jeroglífico que parecía una boca abierta (R). Este símbolo representaba la barra de fracción que usamos hoy (/). Debajo de la "boca abierta", escribían el número que sería el denominador de la fracción.

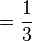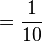Cuando tenían una fracción que no era unitaria (por ejemplo, 2/3), la escribían como una suma de fracciones unitarias distintas. Por eso, a estas sumas se les llama "fracciones egipcias".

La Tablilla de Ajmim: Un Ejemplo Práctico

La tablilla de Ajmim es otro documento antiguo que nos muestra cómo los egipcios trabajaban con fracciones. En ella, se explica cómo dividir una unidad de volumen llamada hekat (que era como una medida de grano, equivalente a 64/64 partes).

La tablilla muestra cómo dividir un hekat entre 3, 7, 10, 11 y 13. Por ejemplo, al dividir un hekat (64/64) entre 3, el escriba obtenía un cociente (el resultado de la división) de 21 y un resto de 1. Luego, reescribía 21 como 16 + 4 + 1. Así, 21/64 se convertía en 16/64 + 4/64 + 1/64, que es igual a 1/4 + 1/16 + 1/64.

El escriba combinaba el cociente y el resto en una sola expresión. Por ejemplo, la respuesta para 1/3 de hekat se escribía como 1/4 1/16 1/64 1 2/3 R. No usaban signos de suma o multiplicación, simplemente ponían las fracciones una al lado de la otra, de izquierda a derecha.

Para demostrar que sus soluciones eran correctas, el escriba multiplicaba las respuestas por los divisores originales y así obtenía de nuevo el valor inicial de 64/64 del hekat.

El Algoritmo de Sylvester: Creando Fracciones Egipcias

Aunque los egipcios tenían sus propios métodos, hoy en día existe un método moderno para convertir cualquier fracción en una fracción egipcia. Se llama el algoritmo voraz de James Joseph Sylvester. Un algoritmo es como una receta o una serie de pasos que se siguen para resolver un problema.

Pasos del Algoritmo

1. Encuentra la fracción unitaria más grande que sea menor o igual a la fracción que quieres convertir. Para encontrar el denominador, divide el número de abajo (denominador) entre el número de arriba (numerador) de tu fracción original. Si hay un resto, súmale 1 al resultado. Si no hay resto, tu fracción ya es unitaria y has terminado. 2. Resta esta fracción unitaria de tu fracción original. 3. Repite los pasos 1 y 2 con la nueva fracción que obtuviste, hasta que el resultado sea una fracción unitaria.

Un Ejemplo Paso a Paso

Vamos a convertir 19/20 en una fracción egipcia usando el algoritmo de Sylvester:

• Paso 1: Queremos convertir 19/20. Dividimos 20 entre 19. El resultado es 1 con un resto. Así que, sumamos 1 al resultado, lo que nos da 2. La primera fracción unitaria es 1/2.
• Paso 2: Restamos 1/2 de 19/20:

19/20 - 1/2 = 19/20 - 10/20 = 9/20.

• Paso 3: Ahora trabajamos con 9/20. Dividimos 20 entre 9. El resultado es 2 con un resto. Sumamos 1 al resultado, lo que nos da 3. La siguiente fracción unitaria es 1/3.
• Paso 4: Restamos 1/3 de 9/20:

9/20 - 1/3 = 27/60 - 20/60 = 7/60.

• Paso 5: Ahora trabajamos con 7/60. Dividimos 60 entre 7. El resultado es 8 con un resto. Sumamos 1 al resultado, lo que nos da 9. La siguiente fracción unitaria es 1/9.
• Paso 6: Restamos 1/9 de 7/60:

7/60 - 1/9 = 21/180 - 20/180 = 1/180. ¡Esta ya es una fracción unitaria! Así que hemos terminado.

Entonces, 19/20 se puede escribir como la fracción egipcia: 1/2 + 1/3 + 1/9 + 1/180

Es importante saber que un mismo número puede tener varias representaciones como fracción egipcia. Por ejemplo, 19/20 también se puede escribir como: 1/2 + 1/4 + 1/5

Galería de imágenes

• 

  Papiro de Ahmes o papiro matemático de Rhind.

Véase también

En inglés: Egyptian fraction Facts for Kids

• Matemáticas en el Antiguo Egipto