Potenciación para niños
La potenciación es una operación matemática que nos ayuda a escribir multiplicaciones repetidas de una forma más corta. Imagina que quieres multiplicar un número por sí mismo varias veces. En lugar de escribir 2 x 2 x 2 x 2 x 2, puedes usar la potenciación.
Esta operación tiene dos partes principales:
- La base (un número grande, por ejemplo, a).
- El exponente (un número pequeño que se escribe arriba y a la derecha de la base, por ejemplo, n).
Se escribe como 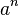 y se lee como "a elevado a la n". Por ejemplo,
y se lee como "a elevado a la n". Por ejemplo, 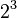 se lee "dos elevado a la tres" o "dos al cubo". Si el exponente es 2, se lee "al cuadrado" (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5^2 , "cinco al cuadrado"). Si es 3, se lee "al cubo" (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^3 , "cuatro al cubo"). Para exponentes mayores, decimos "elevado a la cuarta", "a la quinta", y así sucesivamente.
se lee "dos elevado a la tres" o "dos al cubo". Si el exponente es 2, se lee "al cuadrado" (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5^2 , "cinco al cuadrado"). Si es 3, se lee "al cubo" (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 4^3 , "cuatro al cubo"). Para exponentes mayores, decimos "elevado a la cuarta", "a la quinta", y así sucesivamente.
Contenido
¿Qué es la Potenciación?
La potenciación es una forma abreviada de multiplicar un número por sí mismo varias veces. El número base se multiplica por sí mismo tantas veces como lo indica el exponente.
Por ejemplo, si tenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^4 :
- La base es 3.
- El exponente es 4.
Esto significa que debemos multiplicar el 3 por sí mismo 4 veces: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \times 3 \times 3 \times 3 = 81 .
Potencias con Exponentes Naturales
Cuando el exponente es un número natural (1, 2, 3, 4...), nos dice cuántas veces la base se multiplica por sí misma.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^1 = a (cualquier número elevado a 1 es el mismo número).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^2 = a \times a
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^3 = a \times a \times a
- En general, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^n = \underbrace{a \times a \times \cdots \times a}_{n \text{ veces}}
Esto funciona para cualquier tipo de número, ya sean números positivos, negativos o incluso fracciones.
Multiplicar Potencias con la Misma Base
Cuando multiplicamos potencias que tienen la misma base, mantenemos la base y sumamos los exponentes.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^n \cdot a^m = a^{n+m}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 9^3 \cdot 9^2 = 9^{3+2} = 9^5 (Esto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (9 \times 9 \times 9) \times (9 \times 9) , que son cinco 9s multiplicándose).
Potencia de una Potencia
Si tenemos una potencia elevada a otro exponente, mantenemos la base y multiplicamos los exponentes.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a^m)^n = a^{m \cdot n}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5^2)^3 = 5^{2 \cdot 3} = 5^6 (Esto es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5 \times 5) \times (5 \times 5) \times (5 \times 5) , que son seis 5s multiplicándose).
Potencia de un Producto
Cuando un producto (una multiplicación) está elevado a un exponente, podemos elevar cada factor a ese exponente por separado y luego multiplicarlos.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a \cdot b)^n = a^n \cdot b^n
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2 \times 3)^4 = 2^4 \times 3^4
Potencias con Base Negativa
Si la base es un número negativo, el resultado depende de si el exponente es par o impar:
- Si el exponente es par, el resultado es positivo.
* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-2)^4 = (-2) \times (-2) \times (-2) \times (-2) = 16
- Si el exponente es impar, el resultado es negativo.
* Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (-2)^3 = (-2) \times (-2) \times (-2) = -8
Potencias con Exponentes Negativos
Un exponente negativo significa que debemos tomar el inverso de la base elevada al exponente positivo.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{-n} = \frac{1}{a^n}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 5^{-2} = \frac{1}{5^2} = \frac{1}{25}
Dividir Potencias con la Misma Base
Cuando dividimos potencias que tienen la misma base, mantenemos la base y restamos los exponentes (el exponente de arriba menos el de abajo).
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{a^m}{a^n} = a^{m - n}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{9^5}{9^3} = 9^{5-3} = 9^2
Potencia con Exponente Cero
Cualquier número (excepto el cero) elevado al exponente 0 siempre da como resultado 1.
- Regla:
 (siempre que
(siempre que 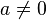 )
) - Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 7^0 = 1
- El caso de
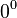 no tiene un valor definido en matemáticas.
no tiene un valor definido en matemáticas.
Potencia de un Cociente
Cuando una división (un cociente) está elevada a un exponente, podemos elevar el numerador y el denominador a ese exponente por separado y luego dividirlos.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left(\frac{a}{b}\right)^n = \frac{a^n}{b^n}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left(\frac{2}{5}\right)^3 = \frac{2^3}{5^3} = \frac{8}{125}
Potencias con Exponentes Fraccionarios
Los exponentes fraccionarios están relacionados con las raíces. Por ejemplo, un exponente de  significa una raíz cuadrada, y un exponente de
significa una raíz cuadrada, y un exponente de  significa una raíz cúbica.
significa una raíz cúbica.
- Regla: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{\frac{1}{n}} = \sqrt[n]{a}
- Ejemplo: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 9^{\frac{1}{2}} = \sqrt{9} = 3
- En general, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{\frac{n}{m}} = \sqrt[m]{a^n}
Potencias con Exponentes Reales
La potenciación también se puede extender a exponentes que son números reales (como 3.14159...). Para esto, se usan conceptos más avanzados de matemáticas, pero la idea principal sigue siendo la misma: una forma de multiplicar un número por sí mismo.
Propiedades que NO cumple la Potenciación
Es importante saber que la potenciación no siempre sigue las mismas reglas que la suma o la multiplicación:
- No es distributiva con la suma o resta: No puedes distribuir el exponente si hay una suma o resta dentro del paréntesis.
* 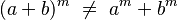 *
* 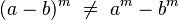
- No es conmutativa: El orden de la base y el exponente importa.
* 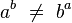 (Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^3 = 8 , pero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^2 = 9 ).
(Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^3 = 8 , pero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^2 = 9 ).
- No es asociativa: El orden en que se agrupan las potencias importa.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a^{b^c} \ \neq\ (a^b)^c (Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2^{3^2} = 2^9 = 512 , pero Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2^3)^2 = 8^2 = 64 ).
Potencias de Base 10
Las potencias de base 10 son muy útiles, especialmente para escribir números muy grandes o muy pequeños.
- Si el exponente es positivo, el número de ceros después del 1 es igual al exponente.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^1 = 10 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^2 = 100 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^6 = 1.000.000
- Si el exponente es negativo, el número de ceros antes del 1 (incluyendo el cero antes de la coma) es igual al valor absoluto del exponente.
* Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{-1} = 0,1 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{-2} = 0,01 * Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^{-6} = 0,000001
Estas potencias se usan en la Notación científica para simplificar la escritura de números muy grandes o muy pequeños. Por ejemplo, 0,00000123 se puede escribir como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 123 \cdot 10^{-8} .
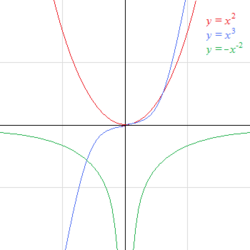
Representación Gráfica de Potencias
Podemos dibujar las potencias en una gráfica. La forma de la curva depende de si el exponente es par o impar.
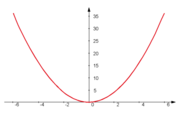
- Si el exponente es par (como
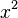 ,
, 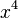 ), la gráfica se parece a una parábola. Es simétrica y tiene su punto más bajo (o más alto) en (0,0).
), la gráfica se parece a una parábola. Es simétrica y tiene su punto más bajo (o más alto) en (0,0). - Si el exponente es impar (como
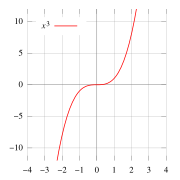
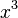 ,
, 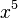 ), la gráfica es una curva que pasa por (0,0) y se extiende en dos direcciones opuestas. Tiene una simetría especial alrededor del punto (0,0).
), la gráfica es una curva que pasa por (0,0) y se extiende en dos direcciones opuestas. Tiene una simetría especial alrededor del punto (0,0).
|
Véase también
 En inglés: Exponentiation Facts for Kids
En inglés: Exponentiation Facts for Kids
- Productos notables
- Raíz cuadrada
- Radicación
- Logaritmo


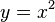 .
. 
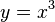 .
.