Porcentaje para niños

El porcentaje es una forma especial de mostrar una parte de un total. Imagina que divides algo en 100 partes iguales. El porcentaje nos dice cuántas de esas 100 partes estamos tomando. Por eso, también se le llama "tanto por ciento", que significa "tantas partes por cada cien".

Usamos el símbolo «%» para representarlo. Este símbolo siempre va después del número, dejando un pequeño espacio. Por ejemplo, si decimos "32 %", significa "32 de cada 100".

Podemos pensar en el porcentaje como una fracción o un número decimal:

• 32 % es lo mismo que la fracción 32/100.
• Y 32/100 es igual a 0,32.

Si queremos calcular el 32 % de 2000, significa que tomamos 32 partes de cada 100 de esas 2000. Para hacerlo, multiplicamos 0,32 por 2000, lo que nos da 640. Así, 640 es el 32 % de 2000.

El porcentaje es muy útil para comparar grupos de diferentes tamaños. Por ejemplo, si en un país hay 500 000 personas con gripe de un total de 10 000 000, y en otro país hay 150 000 enfermos de un total de 1 000 000, es más fácil entender la situación si usamos porcentajes. En el primer país, el 5 % de la gente tiene gripe, mientras que en el segundo, el 15 % la tiene. Esto nos muestra rápidamente que la proporción de enfermos es mayor en el segundo país.

Ejemplos de Porcentajes

Un gráfico circular que muestra el porcentaje de uso de navegadores web en sitios de Wikimedia (abril de 2009 a 2012)

Un porcentaje nos ayuda a entender una parte de un todo. Por ejemplo, 45 % se puede escribir como la fracción 45/100 o como el número decimal 0,45.

¿Cómo se aplica el porcentaje en la vida diaria?

Los porcentajes se usan mucho para hablar de proporciones.

Ejemplo 1: Alumnos en clase

Si el 50 % de los alumnos de una clase son chicos, significa que de cada 100 alumnos, 50 son chicos. Si en total hay 500 alumnos, entonces 250 de ellos son chicos.

Ejemplo 2: Aumento de precio

Imagina que un artículo cuesta 2,50 € y su precio sube 0,15 €. Para saber qué porcentaje de aumento es, dividimos 0,15 entre 2,50, lo que nos da 0,06. Si multiplicamos 0,06 por 100, obtenemos un aumento del 6 %.

Aunque la mayoría de los porcentajes que vemos están entre 0 y 100, un porcentaje puede ser mayor que 100 o incluso negativo. Esto ocurre, por ejemplo, cuando hablamos de cambios o comparaciones.

Historia y Origen del Porcentaje

El concepto de porcentaje es muy antiguo. Ya en el siglo XV, se usaba para calcular impuestos e intereses. Su origen se remonta al Imperio Romano, donde el emperador Augusto estableció un impuesto del 1/100 sobre los bienes vendidos en subastas. Para facilitar los cálculos, ya usaban fracciones que se referían a centenas.

Con el tiempo, especialmente en la Edad Media, los cálculos con un denominador de 100 se hicieron más comunes. A finales del siglo XV y principios del siglo XVI, muchos libros de matemáticas ya incluían estos cálculos para temas como ganancias, pérdidas y tasas de interés. En el siglo XVII, era normal expresar las tasas de interés en centésimas.

¿Cómo evolucionó el símbolo del porcentaje?

El primer símbolo que hacía referencia al «por ciento»

La idea de "por ciento" surgió para simplificar el uso de las fracciones. Era más fácil decir "66 %" que "dos tercios" de una cantidad. Así, la forma de hablar sobre estas proporciones fue cambiando hasta llegar a "por ciento".

Con esta nueva forma de hablar, también surgió la necesidad de escribirlo de manera abreviada. El primer símbolo parecido al actual «%» apareció en un manuscrito anónimo de 1425. Este símbolo fue evolucionando hasta convertirse en el que conocemos hoy.

• 

  Símbolo en el siglo XV

• 

  Símbolo en el siglo XVII

• 

  Símbolo desde el siglo XVIII

El símbolo «%» es una forma estilizada de los dos ceros. Se cree que evolucionó de un símbolo similar que tenía una línea horizontal en lugar de diagonal (alrededor de 1650). Este, a su vez, venía de un símbolo que representaba "P cento" (alrededor de 1425), que significaba "por ciento". La "P" se abrevió y luego desapareció, y "cento" se convirtió en dos círculos separados por una línea, dando origen al símbolo moderno.

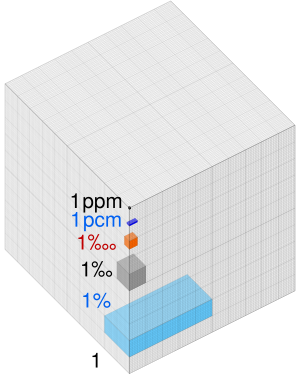
Existen otros símbolos parecidos, como ‰ (por mil) y ‱ (por diez mil o punto básico), que indican que un número se divide por mil o diez mil, respectivamente.

Cálculos con Porcentajes

Para calcular un porcentaje, multiplicamos el valor numérico de la parte por 100 y lo dividimos por el total. Por ejemplo, para saber qué porcentaje son 50 manzanas de un total de 1250 manzanas, primero dividimos 50 entre 1250, lo que da 0,04. Luego, multiplicamos 0,04 por 100 para obtener 4 %.

También podemos multiplicar primero y luego dividir. En el ejemplo anterior, multiplicaríamos 50 por 100 (5000) y luego dividiríamos 5000 entre 1250, lo que también da 4 %.

Porcentaje de un porcentaje

Para calcular un porcentaje de otro porcentaje, convertimos ambos a fracciones de 100 o a números decimales y luego los multiplicamos. Por ejemplo, el 50 % de 40 % se calcula así:

• 50/100 × 40/100 = 0,50 × 0,40 = 0,20 = 20/100 = 20 %.

Es importante no confundir la forma de escribir los porcentajes. Por ejemplo, 25 % es 25/100 o 0,25. No es correcto escribir 25 % / 100, porque eso significaría dividir por 10 000.

Cuando usamos porcentajes, siempre debemos dejar claro a qué se refiere el 100 %.

Ejemplo: Estudiantes de informática

Imagina una universidad donde el 60 % de los estudiantes son mujeres y el 10 % de todos los estudiantes estudian informática. Si el 5 % de las alumnas estudian informática, ¿qué porcentaje de los estudiantes de informática son mujeres?

Primero, calculamos qué porcentaje de todos los estudiantes son mujeres que estudian informática: 60/100 (mujeres) × 5/100 (mujeres que estudian informática) = 3/100, o el 3 % de todos los estudiantes.

Luego, dividimos este 3 % entre el 10 % de todos los estudiantes que estudian informática: 3 % / 10 % = 30/100, o el 30 %. Esto significa que el 30 % de los estudiantes de informática son mujeres.

Representación del Porcentaje

Porcentaje como fracción

Para convertir un porcentaje a fracción, simplemente dividimos el número del porcentaje entre 100 y simplificamos la fracción.

Ejemplo: Para representar el 10 % como fracción:

• 10 % = 10/100 = 1/10 = 0,1

Porcentaje como multiplicación

Para representar una fracción como porcentaje, multiplicamos la fracción por un número que haga que el denominador sea 100. El numerador resultante será el porcentaje.

Ejemplo: Para representar 1/10 como porcentaje:

• 1/10 = 10/100 = 10 %

Cómo Calcular un Porcentaje de un Número

Para encontrar un porcentaje de un número, puedes multiplicarlo por 0,01 (que es lo mismo que 1/100). Por ejemplo, para calcular el 25 % de 150:

• 25 × 0,01 × 150 = 37,5

Otra forma de hacerlo es multiplicar el número por el porcentaje y luego dividir el resultado entre 100.

También puedes usar una regla de tres simple. Por ejemplo, para calcular el 25 % de 150:

• Si 100 % es 150
• Entonces 25 % es x
• Para encontrar x, multiplicamos 150 por 25 y dividimos entre 100: (150 × 25) / 100 = 37,5.

Así, 37,5 es el 25 % de 150.

Porcentaje de Aumento y Disminución

Cuando hablamos de un "aumento del 10 %" o una "disminución del 10 %", generalmente nos referimos al valor inicial. Por ejemplo, si un artículo cuesta 200 € y su precio aumenta un 10 % (que son 20 €), el nuevo precio será 220 €. Este nuevo precio es el 110 % del precio original (100 % + 10 % = 110 %).

Otros ejemplos de cambios porcentuales:

• Un aumento del 100 % significa que la cantidad final es el doble de la original (100 % original + 100 % de aumento = 200 %).
• Un aumento del 800 % significa que la cantidad final es 9 veces la original (100 % + 800 % = 900 %).
• Una disminución del 60 % significa que la cantidad final es el 40 % de la original (100 % – 60 % = 40 %).
• Una disminución del 100 % significa que la cantidad final es cero (100 % – 100 % = 0 %).

En general, si una cantidad cambia en un x por ciento, la cantidad final será (100 + x) por ciento de la cantidad original.

Porcentajes Compuestos

Cuando aplicamos varios cambios porcentuales seguidos, no podemos simplemente sumarlos. Por ejemplo, si un precio sube un 10 % y luego baja un 10 %, el resultado final no es el precio original.

Si un artículo de 200 € sube un 10 % (a 220 €) y luego baja un 10 % (que son 22 € de 220 €), el precio final será 198 €. Esto ocurre porque el segundo porcentaje se calcula sobre una cantidad diferente (220 €), no sobre la original (200 €).

En general, si una cantidad aumenta un x por ciento y luego disminuye un x por ciento, la cantidad final será un poco menor que la original. La disminución neta es el cuadrado del cambio porcentual original (expresado como decimal). En el ejemplo anterior, el precio final de 198 € fue un 1 % menos que el precio inicial de 200 €.

Si los cambios porcentuales son diferentes, por ejemplo, un aumento del x por ciento seguido de un cambio del y por ciento, la cantidad final se calcula multiplicando la cantidad original por (1 + 0,01x) y luego por (1 + 0,01y).

Es importante ser claro al hablar de porcentajes, especialmente en temas como las tasas de interés o los resultados de elecciones. A veces, un "aumento del 5 %" en una tasa de interés puede significar un aumento de 5 puntos porcentuales (por ejemplo, del 10 % al 15 %), no un aumento del 5 % del valor original (que sería del 10 % al 10,05 %). Para evitar confusiones, se usan términos como "puntos porcentuales" o "puntos básicos".

Otros Usos del Porcentaje

La palabra "porcentaje" a veces se usa de forma un poco diferente en los deportes. Por ejemplo, en el baloncesto, se puede decir que un jugador tiene un ".609 porcentaje de tiros de campo". Esto significa que acertó el 60,9 % de sus tiros, no el 0,609 %. Lo mismo ocurre con el "porcentaje de victorias" de un equipo, que se expresa como un decimal (por ejemplo, .500 significa que ganó el 50 % de sus partidos).

El porcentaje también se usa para describir la inclinación de una carretera o vía de tren. Se calcula como 100 × (subida / trayecto). Esto nos dice cuánto sube o baja una carretera por cada 100 unidades de distancia horizontal, expresado en porcentaje.

Además, el porcentaje se utiliza para describir la composición de mezclas, como el porcentaje en masa o el porcentaje en moles.

Unidades Relacionadas

Visualización de 1 %, 1 ‰, 1 ‱, 1 pcm y 1 ppm como fracciones del bloque grande

• Punto porcentual: Diferencia de 1 parte en 100.
• Por mil (‰): 1 parte en 1000.
• Punto base (bp): 1 parte en 10 000.
• Pendiente (geografía)
• Vuelta (ángulo)

Aplicaciones Prácticas

• Porcentaje de panadero
• Porcentaje en volumen

Véase también

En inglés: Percentage Facts for Kids

• Partes por millón
• Por mil (‰)
• Punto base
• Regla de tres