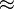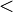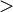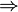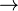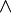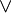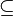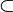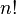Anexo:Símbolos matemáticos para niños
Los símbolos matemáticos son como el lenguaje secreto de las matemáticas. Nos ayudan a escribir ideas complejas de forma corta y clara. Cada símbolo tiene un significado especial y nos permite entender operaciones, relaciones y conceptos importantes.
Contenido
- Símbolos de Aritmética
- Símbolos de Álgebra
- Símbolos de Igualdad y Desigualdad
- Símbolos de Lógica
- Símbolos de Teoría de Conjuntos
- Símbolos de Funciones
- Símbolos de Números
- Símbolos de Geometría Euclidiana
- Símbolos de Combinatoria
- Símbolos de Cálculo Diferencial
- Símbolos de Secuencias y Sucesiones
- Véase también
Símbolos de Aritmética
La aritmética es la parte de las matemáticas que estudia los números y las operaciones básicas que hacemos con ellos, como sumar, restar, multiplicar y dividir.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
|
|
Adición | más | Sumar dos o más números. Por ejemplo, 4 + 6 = 10 significa que si a cuatro le agregamos seis, el resultado es diez. |
| 43 + 65 = 108; 2 + 7 = 9 | |||
 |
Sustracción | menos | Quitar una cantidad a otra. Por ejemplo, 36 − 5 = 31 significa que si a 36 le quitamos 5, el resultado es 31. También se usa para números negativos, como en 36 + (−55) = −19. |
| 36 − 5 = 31; 36 − 55 = −19 | |||
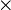  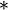 |
Multiplicación | por | Sumar un número varias veces. Por ejemplo, 7 × 6 = 42 significa que si sumamos el 6 siete veces, el resultado es 42. |
| 4 × 6 = 24 o 4 * 6 = 24 o 4 · 6 = 24 | |||
 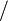 |
División | entre, dividido por | Repartir una cantidad en partes iguales. Por ejemplo, 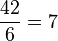 significa que si dividimos 42 en 6 partes iguales, cada parte es de tamaño 7. significa que si dividimos 42 en 6 partes iguales, cada parte es de tamaño 7. |
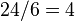 |
|||
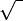 |
Raíz cuadrada | la raíz cuadrada de... | Es el número positivo que, al multiplicarse por sí mismo, da el número original. Por ejemplo, √9 = 3 porque 3 × 3 = 9. |
| √(x²) = |x| | |||
Símbolos de Álgebra
El álgebra usa letras y símbolos para representar números y cantidades, lo que nos permite resolver problemas más complejos.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |\Box| | Valor absoluto | valor absoluto de... | La distancia de un número al cero en la recta numérica, sin importar si es positivo o negativo. Por ejemplo, |−5| = 5 y |5| = 5. |
| |a + bi | = √(a² + b²) | |||
|
|
Sumatorio | suma sobre... | Sumar una serie de números. Por ejemplo, ∑k=14 k² significa sumar los cuadrados de los números del 1 al 4. |
| ∑k=14 k² = 1² + 2² + 3² + 4² = 1 + 4 + 9 + 16 = 30 | |||
 |
Productorio | producto sobre... | Multiplicar una serie de números. Por ejemplo, ∏k=14 (k + 2) significa multiplicar (1+2), (2+2), (3+2) y (4+2). |
| ∏k=14 (k + 2) = (1 + 2)(2 + 2)(3 + 2)(4 + 2) = 3 × 4 × 5 × 6 = 360 | |||
Símbolos de Igualdad y Desigualdad
Estos símbolos nos ayudan a comparar cantidades y expresiones matemáticas.
| Símbolo | Nombre | Se lee | ¿Qué significa? |
|---|---|---|---|
|
|
Igualdad | igual a | Indica que dos expresiones tienen el mismo valor. Por ejemplo, 1 + 2 = 3. |
| 1 + 2 = 6 − 3, 36 + 11 = 47 | |||
|
|
Desigualdad | distinto a | Indica que dos expresiones no tienen el mismo valor. Por ejemplo, 1 + 2 ≠ 4. |
1 + 2 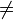 47 47 |
|||
|
|
Aproximación | es aproximadamente igual a | Indica que dos valores son muy parecidos, pero no exactamente iguales. Por ejemplo, π ≈ 3.14159. |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \pi\approx 3,1415924 | |||
|
|
Comparación | es menor que..., es mayor que... | Indica que un número es más pequeño (<) o más grande (>) que otro. Por ejemplo, 3 < 4 (3 es menor que 4) y 5 > 4 (5 es mayor que 4). |
| 3 < 4 5 > 4 | |||
|
|
Comparación | es menor o igual a..., es mayor o igual a... | Indica que un número es menor o igual (≤) o mayor o igual (≥) que otro. Por ejemplo, x ≥ 1 significa que x puede ser 1 o cualquier número más grande. |
| x ≥ 1 ⇒ x² ≥ x | |||
Símbolos de Lógica
La lógica proposicional nos ayuda a analizar cómo se relacionan las afirmaciones y si son verdaderas o falsas.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
|
|
Implicación | implica; si... entonces | Si la primera parte es verdadera, entonces la segunda parte también lo es. Por ejemplo, "Si llueve (A), entonces el suelo se moja (B)". |
| x = 2 ⇒ x² = 4 es verdadera, pero 4 = x² ⇒ x = 2 es, en general, falso (ya que x podría ser −2). | |||
|
|
Doble implicación | si y solo si | Ambas partes son verdaderas o ambas son falsas al mismo tiempo. Por ejemplo, "Puedes votar si y solo si tienes 18 años o más". |
| x + 5 = y + 2 ⇔ x + 3 = y | |||
|
|
Conjunción lógica | y | La afirmación es verdadera solo si ambas partes son verdaderas. Por ejemplo, "Está lloviendo Y hace frío". |
| n < 4 ∧ n > 2 ⇔ n = 3 cuando n es un número natural | |||
|
|
Disyunción lógica | o | La afirmación es verdadera si al menos una de las partes es verdadera. Por ejemplo, "Voy al cine O leo un libro". |
| n ≥ 4 ∨ n ≤ 2 ⇔ n ≠ 3 cuando n es un número natural | |||
|
|
Negación lógica | no | Cambia el valor de verdad de una afirmación. Si "A" es verdadera, "no A" es falsa. |
| ¬(A ∧ B) ⇔ (¬A) ∨ (¬B); x ∉ S ⇔ ¬(x ∈ S) | |||
Símbolos de Teoría de Conjuntos
La teoría de conjuntos estudia colecciones de objetos, llamadas conjuntos.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
|
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{\Box,\Box \} |
Delimitadores de conjunto | el conjunto de... | Se usan para listar los elementos de un conjunto. Por ejemplo, {a, b, c} es el conjunto que contiene a, b y c. |
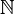 = {0,1,2,3,...} = {0,1,2,3,...} |
|||
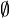  |
Conjunto vacío | conjunto vacío | Es un conjunto que no tiene ningún elemento. Se representa con {} o ∅. |
{n ∈ 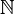 : 1 < n² < 4} = {} : 1 < n² < 4} = {} |
|||
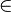 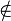 |
Pertenencia de conjuntos | está en; es elemento de | Indica si un elemento pertenece (∈) o no pertenece (∉) a un conjunto. Por ejemplo, 2 ∈ 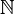 (2 está en los números naturales). (2 está en los números naturales). |
(1/2)−1 ∈ 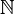 ; 2−1 ∉ ; 2−1 ∉ 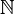 |
|||
|
|
Subconjunto | es subconjunto de | Indica que todos los elementos de un conjunto (A) también están en otro conjunto (B). Si A ⊂ B, significa que A es un subconjunto de B, pero no son el mismo conjunto. |
A ∩ B ⊆ A; 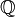 ⊂ ⊂ 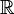 |
|||
 |
Unión de conjuntos | la unión de... y... | Crea un nuevo conjunto con todos los elementos de dos o más conjuntos. |
| A ⊆ B ⇔ A ∪ B = B | |||
|
|
Intersección de conjuntos | la intersección de... y... | Crea un nuevo conjunto con los elementos que dos o más conjuntos tienen en común. |
{x ∈ 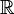 : x² = 1} ∩ : x² = 1} ∩ 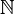 = {1} = {1} |
|||
Símbolos de Funciones
Una función es una regla que asigna a cada elemento de un conjunto (llamado dominio) un único elemento de otro conjunto (llamado codominio).
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
 ![\left[\ \right]](/images/math/3/a/6/3a6a4b52a2ccd7ec58002cb495362e16.png)  |
Aplicación de función; agrupamiento | de | Se usan para agrupar operaciones o para indicar el valor de una función. Por ejemplo, f(x) es el valor de la función f para el valor x. |
| Si f(x) := x², entonces f(3) = 3² = 9; (8/4)/2 = 1, pero 8/(4/2) = 4 | |||
 |
Correspondencia funcional | de... en | Indica que una función f toma valores del conjunto X y los relaciona con valores del conjunto Y. |
Considérese la función 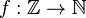 definida por f(x) := x²+1 definida por f(x) := x²+1 |
|||
Símbolos de Números
Los números se clasifican en diferentes conjuntos, cada uno con propiedades especiales.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
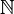 |
Números naturales | N | Son los números que usamos para contar: {0, 1, 2, 3, ...}. A veces, el 0 no se incluye. |
{|a| ∈ Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb Z,a\neq 0 } = 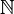 |
|||
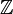 |
Números enteros | Z | Incluyen los números naturales, sus negativos y el cero: {..., −3, −2, −1, 0, 1, 2, 3, ...}. |
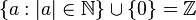 |
|||
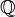 |
Números racionales | Q | Son los números que se pueden escribir como una fracción de dos números enteros (p/q), donde q no es cero. Por ejemplo, 1/2, 3/4, 5. |
3.14 ∈ 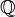 ; π ∉ ; π ∉ 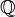 |
|||
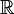 |
Números reales | R | Incluyen todos los números racionales e irracionales (los que no se pueden escribir como fracción, como π o √2). Son todos los números en la recta numérica. |
π ∈ 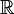 ; √(−1) ∉ ; √(−1) ∉ 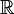 |
|||
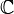 |
Números complejos | C | Son números que tienen una parte real y una parte imaginaria. Se escriben como a + bi, donde 'i' es la raíz cuadrada de -1. |
i = √(−1) ∈ 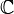 |
|||
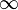 |
Infinito | infinito | Representa una cantidad sin límite, más grande que cualquier número real. Se usa a menudo en cálculos de límites. |
| limx→0 1/|x| = ∞ | |||
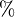 |
Porcentaje | porcentaje de | Una cantidad expresada como una fracción de 100. Por ejemplo, 50% es 50/100. |
| x% = x/100 | |||
Símbolos de Geometría Euclidiana
La geometría euclidiana estudia las formas, tamaños y posiciones de figuras en el espacio.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
|
|
Pi | pi | Es una constante matemática que representa la relación entre la circunferencia de un círculo y su diámetro. Su valor aproximado es 3.14159. |
| A = πr² es el área de un círculo con radio "r" | |||
Símbolos de Combinatoria
La combinatoria es una rama de las matemáticas que estudia las diferentes formas de organizar o combinar elementos de un conjunto.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
|
|
Factorial | factorial de... | Es el producto de todos los números enteros positivos desde 1 hasta un número dado 'n'. Por ejemplo, 4! = 1 × 2 × 3 × 4 = 24. |
| 4! = 24 | |||
Símbolos de Cálculo Diferencial
El cálculo diferencial es una rama de las matemáticas que estudia cómo cambian las funciones y las tasas de cambio.
| Símbolo | Nombre | Se lee como | ¿Qué significa? |
|---|---|---|---|
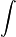 |
Integración | integral de... | Se usa para calcular el área bajo una curva o la acumulación de una cantidad. |
| ∫0b x² dx = b³/3 | |||
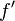 |
Derivación | derivada de f; f prima | Representa la tasa de cambio instantánea de una función en un punto. Es como la pendiente de la línea tangente a la gráfica de la función. |
| Si f(x) = x², entonces f '(x) = 2x | |||
Símbolos de Secuencias y Sucesiones
Las sucesiones son listas ordenadas de números o elementos que siguen un patrón.
| Símbolo | Nombre | Se lee | ¿Qué significa? |
|---|---|---|---|
|
|
Ad infinitum o sucesión | se repite/progresión | Indica que una secuencia de números o elementos continúa siguiendo un patrón, ya sea hasta un punto específico o infinitamente. |
| 1, 2, 3, 4, ... significa que la secuencia de números naturales continúa indefinidamente. | |||
Véase también
 En inglés: Glossary of mathematical symbols Facts for Kids
En inglés: Glossary of mathematical symbols Facts for Kids
- Wikipedia: Cómo se edita una página contiene información acerca de cómo producir símbolos matemáticos en otros artículos matemáticos.