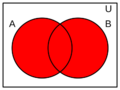
Disyunción lógica para niños
Datos para niños Disyunción lógica |
||
|---|---|---|
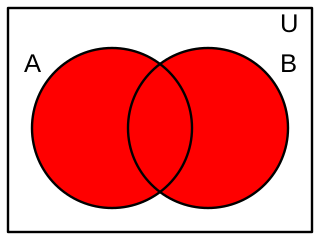 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje natural | A o B | |
| Lenguaje formal |  |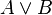
|
| Operador booleano |  |
|
| Operador de conjuntos |  |
|
| Puerta lógica | ||
 |
||
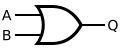| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & A \lor B \ \hline V & V & V \ V & F & V \ F & V & V \ F & F & F \ \end{array} | ||
La disyunción lógica es un concepto fundamental en la lógica y las matemáticas. Se usa para conectar dos ideas o afirmaciones. Imagina que tienes dos frases, como "Hoy es martes" y "Está lloviendo". La disyunción lógica te permite unirlas con la palabra "o".
En lógica, la disyunción se representa con el símbolo 
. También se le conoce como "disyunción inclusiva". Esto significa que la afirmación completa es verdadera si al menos una de las partes es verdadera. Solo es falsa si ambas partes son falsas.
Por ejemplo, si dices "Voy al cine o voy a la biblioteca", esta frase es verdadera si vas al cine, si vas a la biblioteca, o si haces ambas cosas. Solo sería falsa si no vas ni al cine ni a la biblioteca.
Este concepto es muy importante en la informática y la electrónica. Por ejemplo, las computadoras usan "puertas OR" para tomar decisiones.
Contenido
¿Qué es la disyunción lógica?
La disyunción lógica es una operación que combina dos afirmaciones. El resultado de esta combinación puede ser verdadero o falso. Para entenderla mejor, usamos algo llamado "tabla de verdad".
La tabla de verdad de la disyunción
La tabla de verdad nos muestra todos los posibles resultados de una disyunción. Usamos "V" para verdadero y "F" para falso.
Si tenemos dos afirmaciones, A y B, la disyunción "A o B" (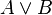) funciona así:
- Si A es verdadera y B es verdadera, entonces "A o B" es verdadera.
- Si A es verdadera y B es falsa, entonces "A o B" es verdadera.
- Si A es falsa y B es verdadera, entonces "A o B" es verdadera.
- Si A es falsa y B es falsa, entonces "A o B" es falsa.
Aquí tienes la tabla de verdad: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{|c|c||c|} \hline A & B & A \lor B \\ \hline F & F & F \\ V & F & V \\ F & V & V \\ V & V & V \\ \hline \end{array}
Como puedes ver, la única forma de que la disyunción sea falsa es que ambas afirmaciones sean falsas.
Símbolos y ejemplos de disyunción
El símbolo más común para la disyunción lógica es , que parece una "v". También se usa la palabra "o" en el lenguaje común.
Algunos ejemplos de cómo se escribe la disyunción:
- a b (se lee "a o b")
- ¬a b (se lee "no a o b")
- a ¬b ¬c d ¬e
En la teoría de conjuntos, la idea similar a la disyunción es la unión de conjuntos.
Propiedades importantes de la disyunción
La disyunción lógica tiene varias propiedades que la hacen predecible y útil. Estas propiedades son como reglas que siempre se cumplen.
- Ley asociativa: No importa cómo agrupes las afirmaciones, el resultado es el mismo.
* (A o B) o C es lo mismo que A o (B o C).
- Existencia del elemento neutro: Si combinas una afirmación con "falso", el resultado es la afirmación original.
* A o Falso es lo mismo que A.
- Ley conmutativa: El orden de las afirmaciones no cambia el resultado.
* A o B es lo mismo que B o A.
- Existe elemento absorbente: Si combinas una afirmación con "verdadero", el resultado siempre es "verdadero".
* A o Verdadero es lo mismo que Verdadero.
Disyunción en operaciones con bits
En la informática, la disyunción se usa mucho con los bits. Un bit es la unidad más pequeña de información y puede ser 0 (falso) o 1 (verdadero).
Veamos cómo funciona la disyunción con bits:
- Cero o cero:
* 0 0 = 0
- Cero o uno:
* 0 1 = 1
- Uno o cero:
* 1 0 = 1
- Uno o uno:
* 1 1 = 1
También se puede aplicar a números más grandes representados en binario (con varios bits):
- Por ejemplo, 1010 1100 = 1110.
* Esto se hace bit a bit: * 1 1 = 1 * 0 1 = 1 * 1 0 = 1 * 0 Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \lor </lor> 0 = 0 == Conexión con la unión de conjuntos == La disyunción lógica está muy relacionada con la [[unión de conjuntos]]. En la [[teoría de conjuntos]], la unión de dos conjuntos A y B (escrito A <math>\cup B) incluye todos los elementos que están en A, o en B, o en ambos.
Por ejemplo, si tienes un conjunto de frutas (Manzana, Pera) y otro de verduras (Zanahoria, Brócoli), la unión de ambos sería (Manzana, Pera, Zanahoria, Brócoli). Si tuvieras un elemento repetido, como (Manzana, Pera) y (Pera, Naranja), la unión sería (Manzana, Pera, Naranja), ya que la Pera está en al menos uno de los conjuntos.
Esta similitud hace que la disyunción lógica y la unión de conjuntos compartan muchas propiedades.
Galería de imágenes
-
Diagrama de Venn de la conectiva
-
Símbolo de la puerta lógica OR
Véase también
En inglés: Disjunction Facts for Kids
- Álgebra booleana
- Lógica proposicional
- XOR (O exclusivo)
- Conjunción lógica
- Operador a nivel de bits
