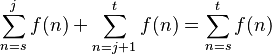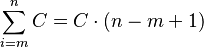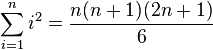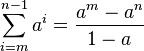Sumatorio para niños
El sumatorio o sumatoria es una forma especial de escribir sumas largas en Matemáticas. Imagina que necesitas sumar muchos números, a veces incluso una cantidad muy grande. Para no tener que escribir todos los números uno por uno, usamos un símbolo especial. Este símbolo es la letra griega sigma mayúscula ( , ∑).
, ∑).
Aunque a veces se usa la palabra "sumatoria", muchos matemáticos prefieren decir simplemente "suma" o "operación de suma" para referirse a esta idea.
Contenido
¿Cómo funciona la notación sigma?
El símbolo sigma mayúscula
La notación con la letra griega sigma mayúscula (Σ) se usa así:
|
|
Esto se lee como "la suma de a sub-i, desde que i vale m hasta que i vale n".
- La letra i es el índice de suma. Es como un contador que va cambiando.
- El número m es el límite inferior. Es el primer valor que toma i.
- El número n es el límite superior. Es el último valor que toma i.
- La expresión a sub-i representa los números que vamos a sumar.
El índice i siempre empieza en m y va aumentando de uno en uno hasta llegar a n. Es importante que m sea menor o igual que n ( ).
).
Casos especiales de la suma
- Si m y n son el mismo número, solo sumamos un término:
- Si m es mayor que n, la suma es cero. Esto es porque no hay números para sumar en ese rango:
El número de términos que se suman es 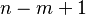 . Por ejemplo, si sumamos desde 1 hasta 6, hay Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6-1+1 = 6 términos.
. Por ejemplo, si sumamos desde 1 hasta 6, hay Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 6-1+1 = 6 términos.
Ejemplos de sumas con sigma
Para sumar los cuadrados de los primeros seis números enteros positivos, escribimos:
La suma de los números no cambia si los ordenamos de otra manera. Esto se debe a propiedades de la suma como la conmutatividad y la asociatividad.
¿Para qué se usa el sumatorio?
Los sumatorios son muy útiles para escribir fórmulas de manera corta y clara. Por ejemplo, para calcular el promedio de un grupo de números, se usa esta expresión:
Aquí, 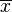 es el promedio,
es el promedio, 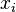 son los números individuales y
son los números individuales y  es la cantidad total de números.
es la cantidad total de números.
Fórmulas para calcular sumas más rápido
A veces, sumar muchos números uno por uno es muy tardado. Por suerte, existen fórmulas que nos ayudan a calcular sumatorios de forma más rápida.
Suma de los primeros números naturales
Para sumar los primeros n números naturales (1, 2, 3, ... hasta n), usamos esta fórmula:
Por ejemplo, para sumar los primeros 1000 números naturales:
Suma de números naturales en un rango
Si quieres sumar números naturales desde un número m hasta un número n, puedes usar esta fórmula: 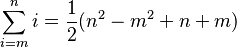 Por ejemplo, para sumar los números del 100 al 200:
Por ejemplo, para sumar los números del 100 al 200: 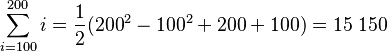
Propiedades importantes de la suma
Los sumatorios tienen reglas que nos permiten manejarlos:
- Si multiplicas cada término por una constante C, puedes sacar la constante fuera del sumatorio:
- Puedes sumar o restar dos sumatorios si tienen los mismos límites:
- Si divides un rango de suma en dos partes, la suma total es la suma de las partes:
Algunas sumas de expresiones con potencias
- Suma de una constante C repetida n-m+1 veces:
- Suma de los cuadrados de los números naturales:
- Suma de los cubos de los números naturales:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sum_{i=1}^n i^3 = \left(\frac{n(n+1)}{2}\right)^2
Algunas sumas con términos exponenciales
Cuando a es un número constante diferente de 1:
- Suma de una serie geométrica:
Errores comunes al usar el término
En español, a veces se usa la palabra "sumatoria" por influencia del inglés. Sin embargo, la forma más tradicional y correcta en español es decir "suma" o "sumatorio". Por ejemplo, decimos "la suma de dos y tres es cinco", no "el sumatorio de dos y tres es cinco".
Véase también
 En inglés: Sum Facts for Kids
En inglés: Sum Facts for Kids
- Productorio
- Serie matemática
- Notación matemática
- Símbolos matemáticos


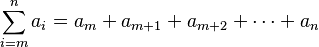
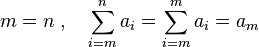
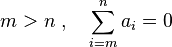
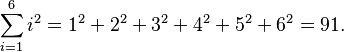
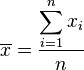
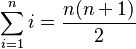
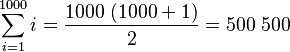
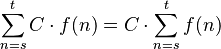
![\sum_{n=s}^t f(n) + \sum_{n=s}^{t} g(n) = \sum_{n=s}^t \left[f(n) + g(n)\right]](/images/math/2/0/7/207fc076b9b57a8845852e18ab6bfe8f.png)