Bicondicional para niños
Datos para niños Bicondicional |
||
|---|---|---|
 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje natural | A si y solo si B A es equivalente a B |
|
| Lenguaje formal |  |
|
| Operador booleano | 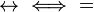 |
|
| Operador de conjuntos |  |
|
| Puerta lógica | ||
 |
||
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & A \leftrightarrow B \ \hline V & V & V \ V & F & F \ F & V & F \ F & F & V \ \end{array} | ||
En el mundo de las matemáticas y la lógica, existe una herramienta especial llamada bicondicional. También se le conoce como equivalencia o doble implicación. Imagina que es como una regla que conecta dos ideas o afirmaciones. Se usa mucho con la frase si y solo si.
Un bicondicional es un tipo de operador lógico. Esto significa que toma dos ideas y las une para formar una nueva idea. Esta nueva idea será verdadera solo si las dos ideas originales tienen el mismo valor de verdad. Es decir, si ambas son verdaderas o si ambas son falsas. Si una es verdadera y la otra falsa, el bicondicional será falso. Es una forma de decir que dos cosas son lógicamente iguales o equivalentes.
Contenido
¿Qué es un Bicondicional?
El bicondicional es una conexión entre dos afirmaciones, que llamaremos p y q. La frase clave es "p si y solo si q".
Para que esta conexión sea verdadera, p y q deben ser ambas verdaderas o ambas falsas al mismo tiempo. Si una es verdadera y la otra es falsa, entonces la conexión bicondicional es falsa.
Piensa en ello como una doble vía. Si vas por un camino, también puedes volver por el mismo camino.
¿Cómo funciona el Bicondicional?
El bicondicional es como decir que la afirmación "p si y solo si q" es lo mismo que decir dos cosas a la vez:
- "Si p es verdadera, entonces q también es verdadera."
- "Y si q es verdadera, entonces p también es verdadera."
Esto se puede escribir con símbolos así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): p \leftrightarrow q \equiv (p\to q) \wedge (q\to p) .
Aquí,  significa "entonces" y
significa "entonces" y 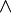 significa "y".
significa "y".
La tabla de verdad explicada
Para entender mejor cómo funciona el bicondicional, usamos una tabla de verdad. Esta tabla nos muestra cuándo la conexión es verdadera (V) o falsa (F).
| p | q |
p ↔ q
|
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | V |
- Si p es verdadera (V) y q es verdadera (V), entonces "p si y solo si q" es verdadera (V).
- Si p es verdadera (V) y q es falsa (F), entonces "p si y solo si q" es falsa (F).
- Si p es falsa (F) y q es verdadera (V), entonces "p si y solo si q" es falsa (F).
- Si p es falsa (F) y q es falsa (F), entonces "p si y solo si q" es verdadera (V).
¿Cómo se representa y se lee?
Una forma de expresar el bicondicional es decir que q es una condición necesaria y suficiente para p. Esto significa que q es indispensable para p, y que q por sí sola es suficiente para que p ocurra.
Símbolos y abreviaturas
En español, a veces se usan abreviaturas como sii, ssi y syss para "si y solo si". Así, "p ↔ q" se puede leer como "p sii q". En inglés, la abreviatura es iff (If and only if).
En Lógica y matemáticas, los símbolos más comunes para el bicondicional son  ,
,  y ≡.
y ≡.
- El símbolo
 se usa a menudo para conectar dos afirmaciones y crear una nueva.
se usa a menudo para conectar dos afirmaciones y crear una nueva. - Los símbolos
 y ≡ se usan más para mostrar que dos afirmaciones son lógicamente equivalentes. El significado exacto puede depender del contexto.
y ≡ se usan más para mostrar que dos afirmaciones son lógicamente equivalentes. El significado exacto puede depender del contexto.
Bicondicional en la tecnología
En el mundo de la lógica digital, que es la base de las computadoras, el bicondicional se puede representar con una "puerta lógica" llamada XNOR. Esta puerta hace exactamente lo mismo: da una salida verdadera solo si sus dos entradas son iguales (ambas 0 o ambas 1).
Ejemplos para entenderlo mejor
Veamos algunos ejemplos para que el bicondicional quede más claro:
- "2 es menor que 10 si y solo si 5 es un divisor de 20."
* "2 es menor que 10" es verdadero. * "5 es un divisor de 20" es verdadero. * Como ambas son verdaderas, el bicondicional es verdadero.
- "5 es mayor que 9 si y solo si la raíz cuadrada de 17 es menor que la raíz cúbica de 6."
* "5 es mayor que 9" es falso. * "La raíz cuadrada de 17 es menor que la raíz cúbica de 6" es falso. * Como ambas son falsas, el bicondicional es verdadero.
Diferencia entre "si" y "si y solo si"
Es muy importante saber la diferencia entre una afirmación que usa "si" y una que usa "si y solo si".
Considera estas dos frases:
- "Una persona es mayor de edad si posee legalmente el carné de conductor."
- "Una persona es mayor de edad si y solo si posee legalmente el carné de conductor."
La primera frase es correcta. Si alguien tiene el carné de conducir de forma legal, ¡seguro que es mayor de edad! No se puede tener el carné legalmente siendo menor.
La segunda frase es incorrecta. ¿Por qué? Porque no es una relación bicondicional. Puedes ser mayor de edad sin tener el carné de conducir. Por ejemplo, una persona de 25 años que nunca ha querido aprender a conducir es mayor de edad, pero no tiene el carné. La frase "si y solo si" implicaría que tener el carné es la única forma de ser mayor de edad, y eso no es cierto.
Véase también
 En inglés: If and only if Facts for Kids
En inglés: If and only if Facts for Kids

