Valor absoluto para niños
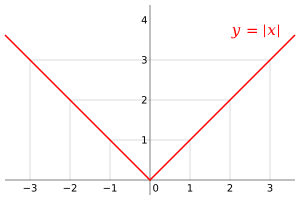
El valor absoluto o módulo de un número real es el valor de ese número sin importar si es positivo o negativo. Imagina una recta numérica: el valor absoluto de un número es la distancia que hay desde ese número hasta el cero. Por ejemplo, el valor absoluto de 3 es 3, y el valor absoluto de -3 también es 3. Se escribe usando dos barras verticales alrededor del número, así: |x|.
El valor absoluto nos ayuda a entender la "cantidad" o "tamaño" de un número, sin preocuparnos por su dirección (si va hacia los números positivos o negativos). Es un concepto muy útil en matemáticas y física, especialmente cuando hablamos de distancia.
Contenido
Valor Absoluto: ¿Qué es y para qué sirve?
El valor absoluto es una herramienta matemática que nos permite medir la "magnitud" de un número. Piensa en ello como la distancia de un punto al origen (cero) en una línea. Como las distancias siempre son positivas o cero, el valor absoluto de cualquier número nunca será negativo.
¿Cómo se define el valor absoluto de un número real?
Para cualquier número real x, el valor absoluto se escribe como |x| y se define de la siguiente manera:
- Si x es un número positivo o cero (por ejemplo, 5 o 0), entonces su valor absoluto es el mismo número x.
* Ejemplo: |5| = 5 * Ejemplo: |0| = 0
- Si x es un número negativo (por ejemplo, -5), entonces su valor absoluto es ese número pero con el signo cambiado a positivo.
* Ejemplo: |-5| = 5 (porque -(-5) es 5)
En resumen, el valor absoluto de x siempre será un número positivo o cero.
Propiedades importantes del valor absoluto
El valor absoluto tiene algunas reglas que siempre se cumplen. Aquí te mostramos las más importantes para cualquier número real a y b:
- Siempre es positivo o cero: El valor absoluto de cualquier número siempre es mayor o igual que cero.
* |a| ≥ 0
- Cero solo si el número es cero: El valor absoluto de un número es cero solo si el número mismo es cero.
* |a| = 0 si y solo si a = 0
- Propiedad de la multiplicación: El valor absoluto de una multiplicación es igual a la multiplicación de los valores absolutos de cada número.
* |a × b| = |a| × |b|
- Desigualdad triangular: El valor absoluto de la suma de dos números es siempre menor o igual que la suma de sus valores absolutos.
* |a + b| ≤ |a| + |b|
Otras propiedades útiles son:
- El valor absoluto de un número negativo es igual al valor absoluto del número positivo.
* |-a| = |a|
- Si el valor absoluto de la diferencia entre dos números es cero, significa que los números son iguales.
* |a - b| = 0 si y solo si a = b
Estas propiedades nos ayudan a resolver problemas y entender mejor cómo funciona el valor absoluto.
El valor absoluto y la distancia
Una de las aplicaciones más importantes del valor absoluto es para calcular distancias.
- El valor absoluto de un número real es la distancia de ese número al cero en la recta numérica.
- El valor absoluto de la diferencia entre dos números (por ejemplo, |a - b|) nos dice la distancia entre esos dos números en la recta numérica. No importa el orden en que los restes, la distancia siempre será la misma.
Valor absoluto de un número complejo
Los números complejos son un tipo de números que tienen una parte real y una parte imaginaria. Aunque no se pueden ordenar como los números reales, también tienen un valor absoluto.
Para un número complejo z = x + iy (donde x es la parte real e iy es la parte imaginaria), su valor absoluto o módulo se calcula como la distancia desde ese número hasta el origen (el punto 0,0) en un plano especial llamado plano complejo. Se usa el Teorema de Pitágoras para calcularlo:
- |z| = √(x² + y²)
Por ejemplo, si tenemos el número complejo 3 + 4i, su valor absoluto sería:
- |3 + 4i| = √(3² + 4²) = √(9 + 16) = √25 = 5
Al igual que con los números reales, el valor absoluto de un número complejo representa su distancia al origen.
Valor absoluto en la programación
En el mundo de la programación, muchos lenguajes de programación tienen una función especial para calcular el valor absoluto. La más común se llama `abs()`. Esta función toma un número y devuelve su valor absoluto. Es muy útil para tareas donde solo nos interesa la magnitud de un valor, como calcular distancias o diferencias.
Por ejemplo, en lenguajes como C, Fortran o Matlab, si escribes `abs(-10)`, el resultado será `10`.
Galería de imágenes
-
El valor absoluto de un número complejo z es la distancia r desde z al origen. Aquí vemos que z y su conjugado z tienen el mismo valor absoluto.
Véase también
 En inglés: Absolute value Facts for Kids
En inglés: Absolute value Facts for Kids