Conjunción lógica para niños
Datos para niños Conjunción lógica |
||
|---|---|---|
 Diagrama de Venn de la conectiva
|
||
| Nomenclatura | ||
| Lenguaje natural | A y B A pero B |
|
| Lenguaje formal | 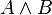 |
|
| Operador booleano | 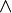 |
|
| Operador de conjuntos |  |
|
| Puerta lógica | ||
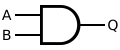 |
||
| Tabla de verdad | ||
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{c|c||c} A & B & A \land B \ \hline V & V & V \ V & F & F \ F & V & F \ F & F & F \ \end{array} | ||
Una conjunción lógica es una forma de unir dos ideas o afirmaciones. Imagina que tienes dos frases, por ejemplo: "Está lloviendo" y "Hace frío". Si las unes con la palabra "y", como en "Está lloviendo y hace frío", estás usando una conjunción.
En el mundo de la lógica y las matemáticas, una conjunción es verdadera solo si todas las afirmaciones que la forman son verdaderas. Si alguna de ellas es falsa, entonces la conjunción completa también es falsa.
El símbolo que se usa para la conjunción lógica es 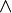 . Es como el signo de la intersección (
. Es como el signo de la intersección ( ) en la teoría de conjuntos, que significa "lo que tienen en común".
) en la teoría de conjuntos, que significa "lo que tienen en común".
En la electrónica, existe algo llamado puerta AND que funciona exactamente como una conjunción lógica.
Contenido
¿Cómo funciona la conjunción lógica?
La conjunción lógica se basa en el valor de verdad de las afirmaciones. Una afirmación puede ser verdadera (V) o falsa (F).
La tabla de verdad
La forma más sencilla de entender la conjunción es con una tabla de verdad. Esta tabla muestra todos los posibles resultados al combinar dos afirmaciones, A y B, con la conjunción (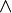 ):
):
- Si A es verdadera (V) y B es verdadera (V), entonces "A y B" es verdadera (V).
- Si A es verdadera (V) y B es falsa (F), entonces "A y B" es falsa (F).
- Si A es falsa (F) y B es verdadera (V), entonces "A y B" es falsa (F).
- Si A es falsa (F) y B es falsa (F), entonces "A y B" es falsa (F).
Como puedes ver, la única manera de que la conjunción sea verdadera es que ambas partes sean verdaderas.
Conjunción en el lenguaje formal
En los lenguajes formales, que son como los idiomas que usan las computadoras o los matemáticos, las afirmaciones representan ideas que pueden ser verdaderas o falsas. Una conjunción lógica es verdadera solo si ambas afirmaciones que la componen son verdaderas.
Conjunción en el álgebra booleana
El álgebra booleana es un sistema matemático que se usa mucho en la informática y la electrónica. Aquí, los valores de verdad se representan con números: 1 para verdadero y 0 para falso.
La conjunción se representa con un punto (·) o simplemente sin nada entre los números. Funciona así:
- 0 · 0 = 0 (Falso y Falso es Falso)
- 0 · 1 = 0 (Falso y Verdadero es Falso)
- 1 · 0 = 0 (Verdadero y Falso es Falso)
- 1 · 1 = 1 (Verdadero y Verdadero es Verdadero)
Propiedades de la conjunción
La conjunción lógica tiene algunas propiedades interesantes que la hacen predecible y útil:
- Ley asociativa: No importa cómo agrupes las afirmaciones. Por ejemplo, (A y B) y C es lo mismo que A y (B y C).
- Elemento neutro: Si unes una afirmación con "verdadero", el resultado es la afirmación original. Por ejemplo, A y Verdadero es igual a A.
- Ley conmutativa: El orden de las afirmaciones no cambia el resultado. A y B es lo mismo que B y A.
- Ley distributiva: La conjunción se puede "distribuir" sobre la disyunción (que es como el "o"). Por ejemplo, A y (B o C) es lo mismo que (A y B) o (A y C).
- Elemento complementario: Si unes una afirmación con su opuesto (no A), el resultado siempre es falso. Por ejemplo, A y (no A) es Falso.
Operaciones con bits
La conjunción es muy importante en la informática para realizar operaciones con bits. Un bit es la unidad más pequeña de información en una computadora, y puede ser 0 o 1.
Veamos algunos ejemplos de cómo funciona la conjunción con bits:
- Cero y cero:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \land 0 = 0 \quad \longleftrightarrow \quad \begin{array}{cc} & 0 \\ \land & 0 \\ \hline & 0 \\ \end{array}
- Cero y uno:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0 \land 1 = 0 \quad \longleftrightarrow \quad \begin{array}{cc} & 0 \\ \land & 1 \\ \hline & 0 \\ \end{array}
- Uno y cero:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 \land 0 = 0 \quad \longleftrightarrow \quad \begin{array}{cc} & 1 \\ \land & 0 \\ \hline & 0 \\ \end{array}
- Uno y uno:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1 \land 1 = 1 \quad \longleftrightarrow \quad \begin{array}{cc} & 1 \\ \land & 1 \\ \hline & 1 \\ \end{array}
- Para cuatro bits:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 1010 \land 1100 = 1000 \quad \longleftrightarrow \quad \begin{array}{ccccc} & 1 & 0 & 1 & 0 \\ \land & 1 & 1 & 0 & 0 \\ \hline & 1 & 0 & 0 & 0 \\ \end{array} Aquí, la operación se hace bit a bit. Por ejemplo, el primer bit de 1010 (que es 1) se compara con el primer bit de 1100 (que es 1). Como 1 y 1 es 1, el primer bit del resultado es 1. El segundo bit de 1010 (0) y el segundo bit de 1100 (1) dan 0, y así sucesivamente.
Galería de imágenes
Véase también
 En inglés: Logical conjunction Facts for Kids
En inglés: Logical conjunction Facts for Kids


