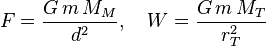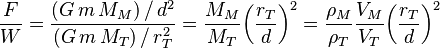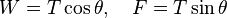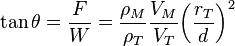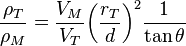Experimento de Schiehallion para niños
El experimento de Schiehallion fue un experimento científico muy importante que se realizó en el Siglo XVIII para calcular la densidad promedio de la Tierra. Tuvo lugar a mediados de 1774 en la montaña escocesa de Schiehallion, en la región de Perthshire. Este experimento, financiado por la Royal Society, consistió en medir los pequeños cambios que sufría un péndulo debido a la fuerza de atracción de la montaña cercana. Después de buscar varias montañas, Schiehallion fue elegida como el lugar ideal porque estaba aislada y tenía una forma simétrica, lo que facilitaba los cálculos.
Isaac Newton ya había pensado en hacer un experimento similar para demostrar su Ley de gravitación universal en su libro Principia, pero al final no lo llevó a cabo. Sin embargo, un grupo de científicos, incluyendo al Astrónomo Real Nevil Maskelyne, estaban convencidos de que el efecto de la montaña sí se podría medir y decidieron realizar el experimento.
El ángulo en que se desviaba el péndulo dependía del tamaño y la densidad de la Tierra y de la montaña. Si se lograba determinar el tamaño y la densidad de Schiehallion, entonces se podría calcular la densidad de la Tierra. Una vez que se conociera la densidad de la Tierra, se podrían estimar las densidades de otros planetas, sus lunas e incluso el Sol, ya que en esa época solo se conocían sus densidades en relación con la de la Tierra. Además, con este experimento se usaron por primera vez las curvas de nivel para estudiar el relieve terrestre, una herramienta muy útil para hacer mapas.
Contenido
¿Qué es el Experimento de Schiehallion y por qué es importante?
Cuando un péndulo está en un lugar donde la gravedad es igual por todos lados, cuelga de forma recta. Pero si se coloca cerca de un objeto muy grande, como una montaña, la fuerza de atracción de esa montaña hará que el péndulo se desvíe un poquito. Esta desviación se puede medir comparándola con la posición de un objeto conocido, como una estrella, y se mide a ambos lados de la montaña. Si se logra calcular el volumen y la densidad promedio de las rocas de la montaña, se puede saber su masa. Con esa información, se puede estimar la densidad promedio de la Tierra y, por lo tanto, su masa.
Isaac Newton había propuesto esta idea en sus Principia, pero pensó que ninguna montaña sería lo suficientemente grande como para desviar el péndulo de forma que se pudiera medir.
Una montaña entera no sería suficiente para producir un efecto notable. Una montaña de [...] tres millas de alto y seis de ancho desviaría el péndulo apenas dos minutos de arco con respecto a la vertical; solamente en los planetas este efecto se podría apreciar.Isaac Newton. Philosophiæ naturalis principia mathematica, 1687.
Aunque Newton calculó que la desviación sería de solo dos minutos de arco, este ángulo, aunque muy pequeño, sí podía ser detectado con los instrumentos de la época.
Realizar este experimento ayudaría a confirmar la ley de gravitación universal de Newton y a obtener estimaciones de la masa y densidad de la Tierra. También permitiría calcular las masas de otros cuerpos celestes, como los planetas, sus lunas o el Sol, ya que en ese tiempo solo se conocían sus masas y densidades en relación con las de la Tierra. Con los datos del experimento también se podría haber encontrado la constante de gravitación universal 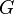 , aunque ese no era el objetivo principal de los científicos. Los valores de esta constante no se obtendrían hasta casi cien años después.
, aunque ese no era el objetivo principal de los científicos. Los valores de esta constante no se obtendrían hasta casi cien años después.
¿Cómo se eligió la montaña para el experimento?
El intento en Chimborazo, 1738
Los primeros en intentar este experimento fueron los astrónomos franceses Pierre Bouguer y Charles Marie de La Condamine. Ellos eligieron el volcán Chimborazo, en lo que hoy es Ecuador, en 1738. Su expedición había ido a América del Sur para medir la longitud de un grado de latitud cerca del ecuador terrestre, pero aprovecharon para intentar el experimento del péndulo. En diciembre de 1738, a pesar del clima difícil, hicieron algunas pruebas a altitudes de 4680 y 4340 metros sobre el nivel del mar.
Bouguer escribió en 1749 que lograron detectar una desviación de 8 segundos de arco, pero no le dieron mucha importancia a los resultados, diciendo que el experimento se podría haber hecho en Francia o Inglaterra en mejores condiciones. Sin embargo, Bouguer señaló que al menos el experimento había demostrado que la Tierra no era una esfera hueca, como algunos creían en ese momento, incluyendo al astrónomo inglés Edmund Halley.
La elección de Schiehallion, 1774

En 1772, el Astrónomo Real Nevil Maskelyne propuso a la Royal Society que se realizara el experimento. Al principio, sugirió montañas en Inglaterra, como Whernside o el macizo de Helvellyn-Skiddaw. La Royal Society creó un comité para estudiar el tema, con miembros como Joseph Banks, Benjamin Franklin y el propio Maskelyne. Este comité encargó al astrónomo Charles Mason la tarea de encontrar una montaña adecuada.
Después de una larga búsqueda a mediados de 1773, Mason informó que la mejor opción era Schiehallion. Esta montaña, de 1083 metros de altura, está entre los lagos Loch Tay y Loch Rannoch, en las Tierras Altas Escocesas. Fue elegida porque estaba aislada, lo que evitaba que otras montañas influyeran en la gravedad, y por la simetría de su ladera de este a oeste, lo que facilitaba calcular su volumen. La gran inclinación de sus laderas de norte a sur permitía tomar las medidas cerca del centro de gravedad de la montaña, maximizando así la desviación del péndulo.
Mason rechazó dirigir el experimento por el sueldo ofrecido. Entonces, el cargo recayó en Maskelyne, quien dejó temporalmente sus deberes como Astrónomo Real. Fue ayudado por los matemáticos Charles Hutton y Reuben Burrow. Contrataron trabajadores para construir los observatorios y una cabaña para los científicos. Entre los instrumentos había un cuadrante de 30 cm, un sector cenital (un tipo de telescopio) de 3 metros y un reloj de péndulo muy preciso. También compraron un teodolito y una cadena de Gunter para estudiar la montaña, además de dos barómetros para medir altitudes. La Royal Society financió generosamente el experimento.
¿Cómo se hicieron las mediciones?
Mediciones astronómicas
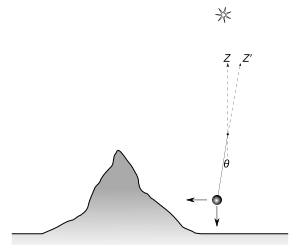
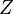 , determinado con astrometría, y el cénit aparente
, determinado con astrometría, y el cénit aparente 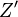 , según la posición de la plomada.
, según la posición de la plomada.Se construyeron dos observatorios, uno al norte y otro al sur de la montaña, y una cabaña para los científicos. La mayoría de los trabajadores se alojaron en tiendas de campaña. Las mediciones astronómicas de Maskelyne fueron las primeras. Para ello, tuvieron que determinar las distancias al cénit (el punto directamente encima del observador) de varias estrellas cuando pasaban exactamente por el sur. Las condiciones climáticas a menudo eran difíciles, con niebla y lluvia. Aun así, el observatorio del sur logró 76 mediciones de 34 estrellas en una dirección y 93 de 39 estrellas en la otra. El del norte obtuvo 68 y 100 observaciones de 32 y 37 estrellas, respectivamente. Para evitar errores, hicieron varias mediciones con el telescopio apuntando al este y luego al oeste.
Para calcular la desviación causada por la montaña, fue necesario considerar la curvatura de la Tierra. Maskelyne calculó que la diferencia entre los cénit locales de los observadores al norte y al sur de la montaña sería de 54.6 segundos de arco. Después de que los topógrafos midieran una diferencia de 42.94" de latitud entre los dos observatorios, Maskelyne pudo restar esta parte y finalmente calcular la diferencia en la desviación medida: 11.6".
Maskelyne publicó los resultados iniciales en 1775. Calculó que, si la densidad de Schiehallion y la de la Tierra fueran iguales, la atracción de la Tierra sobre el péndulo sería 9933 veces la de la montaña. Como el resultado obtenido era la mitad de este valor, concluyó que la densidad promedio de la Tierra era aproximadamente el doble que la de Schiehallion.
Maskelyne escribió que la ley de gravitación universal de Newton había sido confirmada, ya que se demostró que las montañas sí producían una atracción gravitacional. La Royal Society le otorgó a Maskelyne la Medalla Copley en 1775.
Mediciones topográficas
El trabajo de topografía fue complicado por el mal tiempo y se extendió hasta 1776. Para calcular el volumen de la montaña, fue necesario dividirla en muchas secciones verticales y calcular el volumen de cada una. Para esta tarea, dirigida por Charles Hutton, los topógrafos tomaron miles de medidas en cientos de puntos de la montaña. Para organizar todos los datos, crearon líneas que unían puntos a la misma altura. Así, no solo determinaron las alturas de las secciones, sino que también obtuvieron una idea clara del terreno. Hutton había inventado las curvas de nivel, que se usarían mucho en la elaboración de mapas.
| Tabla de densidades del Sistema Solar de Hutton | ||
|---|---|---|
| Objeto | Densidad, kg·m−3 | |
| Hutton, 1778 | Valor actual | |
| Sol | 1100 | 1408 |
| Mercurio | 9200 | 5427 |
| Venus | 5800 | 5204 |
| Tierra | 4500 | 5515 |
| Luna | 3100 | 3340 |
| Marte | 3300 | 3934 |
| Júpiter | 1100 | 1326 |
| Saturno | 410 | 687 |
Hutton pasó dos años calculando las atracciones individuales de cada sección de la montaña. En 1778, publicó sus resultados. Calculó que la densidad de Schiehallion era de 2500 kg·m−3. Con base en esto, determinó que la densidad de la Tierra era de 4500 kg·m−3. Este valor es un 20% diferente del valor aceptado hoy (5515 kg·m−3).
El hecho de que la densidad promedio de la Tierra fuera mucho mayor que la de las rocas de la superficie significaba que había capas más densas en sus profundidades. Hutton supuso correctamente que el núcleo terrestre debía estar hecho de materiales metálicos y que podría tener una densidad de unos 10 000 kg·m−3. Según sus cálculos, esta parte metálica ocuparía el 65% del diámetro de la Tierra. Con la densidad promedio de la Tierra ya calculada, Hutton pudo asignar valores a las densidades de los planetas a partir de los valores relativos que ya se conocían.
¿Se ha repetido el experimento de Schiehallion?
En 1798, 24 años después del experimento de Schiehallion, Henry Cavendish encontró una forma más precisa de determinar la densidad promedio de la Tierra. Usando una balanza de torsión muy sensible para medir la atracción entre dos grandes masas de plomo, Cavendish obtuvo un valor de 5448 ± 0.033 kg·m−3. Este resultado solo se mejoró en 1895, cuando Charles Boys obtuvo un valor de 5527 kg·m−3 con un dispositivo similar, pero mejorado con fibras muy finas de cuarzo.
En 1811, John Playfair hizo un segundo estudio de Schiehallion. Sugirió una densidad entre 4560 y 4870 kg·m−3, aunque Hutton defendió su valor original en 1821. Los cálculos de Playfair mejoraron el valor de la densidad, pero seguía siendo bajo y menos preciso que el de Cavendish.

El experimento de Schiehallion se repitió en 1856 por Henry James, director general de la Ordnance Survey. Esta vez eligió la montaña Arthur's Seat, en Edimburgo. Con los recursos de la Ordnance Survey, James amplió el estudio topográfico a 21 kilómetros a la redonda. Obtuvo una densidad de 5300 kg·m−3.
En 2005, se hizo una variación del experimento de 1774. En lugar de calcular las diferencias locales en el cénit, se comparó con mucha precisión el tiempo que tardaba un péndulo en oscilar en la cima y en la base de Schiehallion. El tiempo de oscilación de un péndulo está relacionado con la aceleración de la gravedad local. En lo alto de la montaña, la gravedad es menor, por lo que el péndulo se movería más lentamente, pero la masa de la montaña ayuda a reducir esta diferencia. Este experimento es más sencillo que el original, pero requiere una precisión muy alta. El experimento dio un valor para la masa de la Tierra de 8.1 ± 2.4 × 1024 kg, lo que corresponde a una densidad promedio de 7500 ± 1900 kg·m−3.
Desde el experimento de 1774, se han podido revisar los datos geofísicos, y ahora se pueden considerar factores que antes no eran posibles. Gracias a un modelo digital del terreno que cubre una región de 120 km de radio, se ha mejorado el conocimiento de la geología de Schiehallion. Con la ayuda de una computadora en 2007, se determinó que la densidad promedio de la Tierra es de 5480 ± 250 kg·m−3. Comparado con el valor actual de 5515 kg·m−3, se nota la gran precisión de las mediciones astronómicas de Maskelyne.
¿Cómo se calcula la densidad de la Tierra?
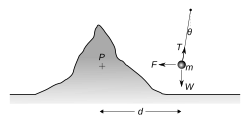
Para simplificar el experimento, solo se analiza la atracción en un lado de la montaña. Un plomada (una pesa que cuelga de un hilo) de masa 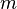 está a una distancia
está a una distancia 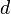 del centro de gravedad
del centro de gravedad  de la montaña, que tiene masa
de la montaña, que tiene masa 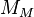 y densidad
y densidad 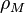 . La plomada se desvía un pequeño ángulo
. La plomada se desvía un pequeño ángulo 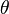 debido a la fuerza de atracción
debido a la fuerza de atracción 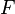 que la montaña ejerce hacia
que la montaña ejerce hacia  . El peso de la plomada,
. El peso de la plomada, 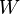 , apunta hacia el centro de la Tierra. La suma de las fuerzas
, apunta hacia el centro de la Tierra. La suma de las fuerzas 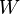 y
y 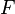 es la tensión
es la tensión 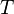 del hilo del péndulo. La Tierra tiene masa
del hilo del péndulo. La Tierra tiene masa 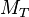 , radio
, radio 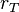 y densidad
y densidad 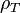 .
.
Las dos fuerzas gravitatorias sobre la plomada se calculan con la ley de gravitación universal de Newton:
Donde 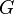 es la constante de gravitación universal. Si dividimos ambas fuerzas,
es la constante de gravitación universal. Si dividimos ambas fuerzas, 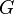 y
y 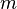 se eliminan:
se eliminan:
Aquí, 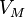 y
y 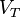 son los volúmenes de la montaña y de la Tierra, respectivamente. Cuando el péndulo está en equilibrio, las partes vertical y horizontal de la tensión del hilo
son los volúmenes de la montaña y de la Tierra, respectivamente. Cuando el péndulo está en equilibrio, las partes vertical y horizontal de la tensión del hilo 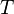 se relacionan con las fuerzas gravitatorias y el ángulo de desviación
se relacionan con las fuerzas gravitatorias y el ángulo de desviación 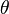 :
:
Así obtenemos:
Como conocemos los valores de 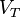 ,
, 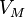 ,
, 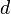 y
y 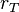 , al medir el ángulo de desviación
, al medir el ángulo de desviación 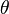 podemos obtener un valor para la relación
podemos obtener un valor para la relación 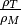 :
:
Galería de imágenes
-
Chimborazo, en Ecuador, fue el emplazamiento del experimento de 1738.
-
La simetría de Schiehallion vista desde Loch Rannoch.
-
El ángulo de desviación es la diferencia entre el cénit real
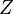 , determinado mediante astrometría, y el cénit aparente
, determinado mediante astrometría, y el cénit aparente 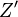 , según la posición de la plomada.
, según la posición de la plomada. -
Arthur's Seat, en Edimburgo, fue el lugar elegido por Henry James en 1856 para repetir el experimento.
Véase también
 En inglés: Schiehallion experiment Facts for Kids
En inglés: Schiehallion experiment Facts for Kids
- Péndulo simple.
- Ley de gravitación universal.
- Experimento de Cavendish.