Silogismo para niños
El silogismo (en latín: syllogismus) es un tipo de razonamiento deductivo que hace parte de la lógica de origen griego. Consta de dos proposiciones como premisas y otra como conclusión, siendo la última una inferencia necesariamente deductiva de las otras dos. Fue formulado por primera vez por Aristóteles. El silogismo es la noción central de la lógica aristotélica, pilar fundamental del pensamiento científico y filosófico desde su invención hace más de dos milenios.
Aristóteles consideró a los silogismos en su obra lógica recopilada Órganon, en los libros conocidos como Primeros Analíticos (en griego Proto Analytika, en latín Analytica Priora — idioma con el que se conoció la obra en Europa Occidental).

Contenido
- Los silogismos según Aristóteles
- Elementos
- Reglas del silogismo
- Reglas para los términos
- Reglas de las proposiciones
- De dos premisas negativas no puede obtenerse conclusión alguna
- De dos premisas afirmativas no puede sacarse una conclusión negativa
- La conclusión siempre sigue la parte más débil. Se entiende por parte débil a la negativa frente a la afirmativa, y a la particular frente a la universal
- De dos premisas particulares no se obtiene conclusión válida
- Modos válidos
- Representación gráfica de los modos como lógica de clases mediante diagramas de Venn
- Problemática de la lógica silogística
- El silogismo en la lógica formal
- Véase también
Los silogismos según Aristóteles
Aristóteles consideraba la lógica como un método de relación de términos. Los silogismos aristotélicos buscan establecer la relación entre dos términos: un sujeto y un predicado, los cuales se unen o separan en juicios. La aparición de posibles conclusiones sobre la relación entre estos dos términos surge de su comparación, por medio de juicios, con un tercer término que hace de "término medio" (tertium comparationis). Así pues, el silogismo consta de dos juicios, premisa mayor y premisa menor, en los que se comparan tres términos (sujeto, predicado y "término medio"), de cuya comparación se obtiene un nuevo juicio como conclusión.
La lógica silogística trata de establecer las leyes que garantizan que, de la verdad de los juicios comparados, o premisas, se pueda obtener con garantía de verdad un nuevo juicio verdadero, o conclusión.
Elementos
De acuerdo a lo explicado en el párrafo previo los elementos de un silogismo son:
- Un término sujeto S.
- Un término predicado P.
- Un término medio M,.
- Un antecedente, el cual consta de dos juicios llamados premisas.
- Un consecuente, el juicio resultante como conclusión.
Estructura
Un silogismo posee la siguiente estructura:
- Premisa mayor, juicio en el que se encuentra el término mayor o predicado de la conclusión, P, comparado con el término medio M.
- Premisa menor, juicio en el que se encuentra el término menor o sujeto de la conclusión, S, comparado con el término medio M.
- Consecuente o conclusión, juicio al que se llega, el cual afirma (une) o niega (separa) la relación entre S y P.
Los juicios, que dan origen a las premisas mayor y menor, relacionan los términos unos con otros para constituir el argumento. De esta manera, el silogismo argumenta estableciendo la conclusión como una relación entre dos términos, derivada de la comparación de ambos términos con un tercer término.
Cantidad, o extensión de los términos
La extensión de los términos se refiere a un criterio de cantidad. Los términos S, P y M pueden ser tomados en su extensión universal, abarcando a todos los posibles individuos - el dominio de discurso - a los cuales pueda referirse el concepto, o en su extensión particular, cuando se refiere sólo a algunos. Por ejemplo, la relación entre S y P de acuerdo a su extensión puede ser:
- Universal: donde todo S es P. Los nombres propios tienen extensión universal; pues el uno, como único, equivale a un individuo que siendo único es, por eso, todos los posibles.
- Particular: donde algunos S son P
Cualidad, o relación entre términos
Específicamente, la cualidad o relación entre términos puede ser:
- Afirmativa o de unión: S es P.
- Negativa o de separación: S no es P.
El predicado de una afirmación siempre tiene extensión particular, y el predicado de una negación está tomado en su extensión universal. Cuando un concepto, sujeto o predicado, está tomado en toda su extensión se dice que está distribuido; cuando no, se dice que está no distribuido.
Clasificación de los juicios
Según el criterio de cantidad y cualidad, los juicios o premisas pueden agruparse en las siguientes clases:
| Clase | Denominación | Esquema | Expresión-Ejemplo | Extensión de los términos |
| A | Universal Afirmativo | Todo S es P | Todos los hombres son mortales | S: Universal P: Particular |
| E | Universal Negativo | Ningún S es P | Ningún hombre es mortal | S: Universal P: Universal |
| I | Particular Afirmativo | Algún S es P | Algún hombre es mortal | S: Particular P: Particular |
| O | Particular Negativo | Algún S no es P | Algún hombre no es mortal | S: Particular P: Universal |
El nombre de las clases A e I deriva del verbo adfirmo (en latín: afirmo) y el de las E y O de nego (en latín: niego).
Figuras y modos silogísticos
Teniendo en cuenta la disposición de los términos en las premisas y en la conclusión se pueden dar las siguientes figuras silogísticas:
| Elemento | 1ª Figura | 2ª Figura | 3ª Figura | 4ª Figura |
| Premisa mayor | M P | P M | M P | P M |
| Premisa menor | S M | S M | M S | M S |
| Conclusión | S P | S P | S P | S P |
Los modos silogísticos son las distintas combinaciones que se pueden hacer con los juicios que forman parte de las premisas y la conclusión. Como los juicios tienen cuatro clases distintas (A,E,I,O), y para formar figuras se toman de tres en tres —dos premisas y una conclusión— hay 64 combinaciones posibles. Estas 64 combinaciones posibles quedan reducidas a 19 modos válidos, al aplicar las reglas del silogismo.
Reglas del silogismo
Cuando se comete un error en el silogismo el resultado es una falacia.
Reglas para los términos
El silogismo no puede tener más de tres términos
Este principio se limita a cumplir la estructura misma del silogismo: la comparación de dos términos con un tercero. Aunque la regla es clara, su aplicación no siempre lo es. Es lo que algunos llaman silogismo de cuatro patas, ya que se introduce equivocadamente un cuarto término o quaternio terminorum.
Ejemplo: si se analiza el siguiente silogismo erróneo:
| Premisa Mayor | Todos los seres libres son hombres |
| Premisa Menor | Ninguna mujer es hombre. |
| Conclusión | Ninguna mujer es libre. |
Los términos que aparecen como evidentes son las palabras hombre, libre, mujer. Pero, a modo de non sequitur (un tipo de error lógico) en la supuesta premisa mayor se utiliza la palabra hombre en su acepción de especie (Homo sapiens) mientras que en la supuesta premisa menor del quaternio terminorum se ha trocado el significado de la palabra hombre utilizando la acepción de género (hombre como sinónimo de varón). Es decir, se ha incluido subrepticiamente un cuarto término, de allí que la conclusión del quaternio terminorum es errónea, un sofisma.
Los términos no deben tener mayor extensión en la conclusión que en las premisas
Por la misma estructura del silogismo; únicamente podremos obtener conclusiones acerca de lo que hemos comparado en las premisas.
El término medio no puede entrar en la conclusión
Por la misma estructura del silogismo la función del término medio es servir de intermediario, como término de la comparación.
Ejemplo: El axioma matemático citado lo podemos representar así:
A = B
B = C
∴ A = C
Vemos que el papel del término medio (B) es el de la tercera cantidad, es decir, igualar a los dos extremos. O sea, su oficio es evidenciar la relación que existe entre el término mayor (C) y el menor (A). Por tanto, nada tiene que hacer en la conclusión; su verdadero lugar está en las premisas como antecedente.
El término medio ha de tomarse en su extensión universal por lo menos en una de las premisas
Para que la comparación sea tal, es necesario que el término medio sea comparado en su totalidad. De otra forma, podría ser comparado un término con una parte y el otro con la otra, constituyéndose en realidad entonces un silogismo de cuatro términos.
Ejemplo: Consideremos el siguiente silogismo erróneo:
| Premisa Mayor | Todos los andaluces son españoles. |
| Premisa Menor | Algunos españoles son gallegos. |
| Conclusión | Por tanto, algunos gallegos son andaluces. |
Lo que evidentemente no es un modo válido, puesto que "españoles" en la premisa mayor al ser predicado de una afirmativa está tomado en su extensión particular.
Reglas de las proposiciones
De dos premisas negativas no puede obtenerse conclusión alguna
Dos premisas negativas no se adaptan a la estructura del silogismo, ya que si negamos S de M, y P de M, no sabemos qué relación puede haber entre S y P. Para establecer la relación, por lo menos uno de los términos tiene que identificarse con M. Por tanto una de las dos premisas tiene que ser afirmativa.
De dos premisas afirmativas no puede sacarse una conclusión negativa
En efecto, si S se identifica con M, y P también se identifica con M, no tiene sentido establecer una relación negativa con entre S y P. La conclusión será afirmativa.
La conclusión siempre sigue la parte más débil. Se entiende por parte débil a la negativa frente a la afirmativa, y a la particular frente a la universal
Veamos los dos casos separadamente:
- Si se afirma una relación entre dos términos (X, M), pero se niega la de uno de ellos con otro (Y, M), siendo M el término medio, no puede haber más conclusión que negar la relación que pueda haber entre el primero (X) y el último (Y) siendo uno sujeto y el otro predicado de la conclusión.
- Pueden darse dos casos: Que una sea afirmativa y la otra negativa, o que las dos sean afirmativas.
- Dos afirmativas. (El predicado de una afirmativa está tomado en su extensión particular, y el predicado de una negativa en su extensión universal).
Al ser ambas afirmativas sus predicados son particulares. El término de la universal tiene necesariamente que ser el término medio, la conclusión debe tener un sujeto particular. - Una afirmativa y otra negativa: tiene que haber dos términos universales. Uno de ellos tiene que ser el término medio, el otro tiene que ser el predicado de la conclusión, pues la conclusión tendrá que ser negativa, (caso a) de esta misma regla). Por tanto el término que queda será el sujeto de la conclusión con extensión particular.
- Dos afirmativas. (El predicado de una afirmativa está tomado en su extensión particular, y el predicado de una negativa en su extensión universal).
De dos premisas particulares no se obtiene conclusión válida
También tiene dos casos posibles: que una sea afirmativa y la otra negativa o que ambas sean afirmativas.
- Sólo hay un término universal que es el predicado de la negativa, que por tanto tiene que ser el término medio. La conclusión tendrá que ser negativa (caso a) de la regla anterior), y por tanto el predicado tendrá que ser universal, y no puede ser el término medio por tanto no puede haber conclusión.
- Los tres términos son particulares, y por tanto no puede haber término medio con extensión universal, y por tanto no hay conclusión posible.
Modos válidos
El modo del silogismo es la forma que toma este de acuerdo con la cantidad y la cualidad de las premisas y la conclusión. De la aplicación de las leyes de los silogismos a los 64 modos posibles resultan válidos solamente 19 y son los que tradicionalmente se memorizan atendiendo a los modos válidos de cada figura con sus premisas y conclusión.
| Así los modos válidos | Se memorizaban cantando | |
| De la primera figura | AAA, EAE, AII, EIO | BARBARA, CELARENT, DARII, FERIO |
| De la segunda figura | EAE, AEE, EIO, AOO | CESARE, CAMESTRES, FESTINO, BAROCO |
| De la tercera figura | AAI, IAI, AII, EAO, OAO, EIO | DARAPTI, DISAMIS, DATISI, FELAPTON, FERISON, BOCARDO |
| De la cuarta figura | AAI, AEE, IAI, EAO, EIO | BAMALIP, CAMENES, DIMARIS, FRESISON, FESAPO |
Nota bene: También son válidos para la primera figura los modos subalternos BARBARI, CELARONT; para la segunda: CESARO, CAMESTROP; y para la cuarta: CAMENOP.
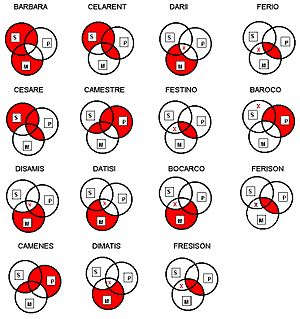
Representación gráfica de los modos como lógica de clases mediante diagramas de Venn
Se pueden representar estos modos mediante diagramas de Venn con las siguientes convenciones:
- Cada término del silogismo está representado por S, P, M, por un círculo incoloro que representa a todos los miembros posibles de una clase.
- La conclusión aparece como resultado de la relación de los términos S y P en su relación con M.
- La inexistencia se muestra como zona rellena de color.
- La existencia individual se afirma mediante una X: Al menos uno, o algunos.
- La relación de los términos se constituye como pertenencia o no pertenencia a la clase.
- La relación de inclusión, Todo S es P, se representa como “No hay ningún S que no sea P” según muestra la imagen que se muestra al margen.
Teniendo en cuenta la problemática de la lógica aristotélica, de la que se habla más adelante, el problema del "compromiso existencial" afecta a los modos Darapti, Felapton, Bramalip, y Fesapo que no se muestran en las gráficas, al no ser admitidos como válidos por algunos y, sobre todo, la representación gráfica no hace plausible la conclusión, debido a la falta de "compromiso existencial", como se comenta más adelante.
Problemática de la lógica silogística
La exposición anterior es la forma más simple y esquemática tradicionalmente presentada como lógica aristotélica.
Sin embargo, la problemática que trata Aristóteles es bastante más compleja. Aristóteles define:
Silogismo es un argumento en el cual, establecidas ciertas cosas, resulta necesariamente de ellas, por ser lo que son, otra cosa diferente.Aristóteles An. Pr. I 24 b 18-23
Dos aspectos a destacar en su definición:
- La necesidad, que considera el silogismo como categórico, por considerar que los juicios que lo integran son asimismo categóricos.
- El fundamento de dicha necesidad, por "ser las cosas lo que son".
Hablar del silogismo categórico supone hablar de lo necesario e incondicionado. Y precisamente incondicionado por estar basado en el “ser de las cosas”.
Aristóteles está pensando en un predicado aprehendido a partir de la experiencia y atribuido por el entendimiento a un sujeto. En el lenguaje apofánticoel silogismo manifiesta la verdad, porque el entendimiento humano (entendimiento agente, según Aristóteles) es capaz de llegar a la intuición directa de lo realaunque sea a través de un proceso de abstracción.
Se parte del supuesto de que P es predicado “verdadero” de S (en el sentido de que P manifiesta la "identidad" del ser de S), lo que plantea una cuestión metalógica. Véase verdad.
Aristóteles piensa que el juicio manifiesta “lo que es” como verdadero. El problema entonces es ¿y cómo se predica de un sujeto lo que “no-es”?(V.:aporética).
La lógica aristotélica se encuentra con el problema de los juicios negativos que resuelve no del todo bien.
De hecho en el cuadro de oposición de los juicios Aristóteles estudió con todo detalle problemas que posteriormente no se han tenido en cuenta; en realidad consideró tres figuras y no todos los 19 modos válidos. Aristóteles considera modos perfectos aquellos cuya validez aparece como evidente, siendo los demás imperfectos por cuanto deben ser probados por medio de los modos perfectos, que son los correspondientes a la primera figura: BÁRBARA, CELARENT, DARII, FERIO.
Incluso llegó a considerar tales modos como los axiomas de todo el sistema lógico.
El juicio como “atribución” de un predicado verdadero a un sujeto, (en el sentido de que P manifiesta la "identidad" como "ser del sujeto", en tanto que realidad conocida), plantea el problema de un predicado falso, es decir un no-predicado. ¿Cómo conocemos un no-predicado?…
Lingüísticamente, el problema se disfraza negando el verbo en lugar del predicado como atributo (gramática). De esta forma en vez de decir "Antonio es un no-caballo", (¿qué es un no-caballo?), decimos "Antonio no es un caballo". Pero esto segundo sólo es inteligible bajo el punto de vista extensional de los conceptos, es decir bajo el punto de vista de ser un elemento de un conjunto definido por una propiedad, o lo que es lo mismo por su pertenencia o no-pertenencia a una determinada clase; lo que nos lleva a la lógica de clases.
La lógica moderna simbólica, meramente lógica formal, no tiene conexión con contenido de verdad alguno y supera con claridad estas dificultades; sobre todo con la ventaja de poder tratar proposiciones poliádicas, llamadas así porque tienen más de dos términos (por ejemplo: "Júpiter es mayor que la Tierra y menor que el Sol"), y facilitar enormemente el cálculo lógico, por lo que, de hecho, la lógica aristotélica, como tal, está en claro desuso.
Hans Reichenbach estudia el cuadro de oposición de los juicios considerando los juicios A, E, I, O, como relación de clases y considera que pueden eliminarse los juicios negativos E, O, que son los problemáticos, mediante la anotación de la negación de la clase complementaria.
La notación se hace estableciendo entre el sujeto S y el predicado P, la letra minúscula correspondiente al tipo de juicio. Así tenemos que:


Así no sólo se simplifica la notación sino que de modos que tradicionalmente han sido considerados inválidos, se puede obtener conclusión válida, que la notación clásica hacía imposible.
Por todo ello la interpretación actual de la lógica aristotélica como silogismo es su interpretación como lógica de clases. Tal es el mérito de la obra de Lukasiewicz.
Pero considerar los conceptos universales, como clases plantea el problema de la existencia del individuo como instanciación o compromiso existencial. Pues la clase como propiedad independiente puede considerarse como abstracto universal. Pero los predicados, como atributos, no tienen sentido sin un sujeto gramatical del cual se prediquen porque posea dicha propiedad.
La lógica tradicional no consideraba el problema de la existencia o no existencia del individuo respecto a los conceptos universales, pues se supone que éstos han surgido de la abstracción a partir del conocimiento de los singulares o individuos existentes.
El silogismo en la lógica formal
La lógica formal actual considera la relación S y P como una relación meramente sintáctica sin contenido material alguno, bien sea en una relación de clases o una función proposicional de predicados. Aristóteles considera dicha formalidad, desde luego, bajo el punto de vista de la relación entre dos términos S (sujeto) y P (predicado) que al mismo tiempo tienen una función lingüístico-gramatical, pues para Aristóteles los términos representan aspectos del ser y por tanto de la realidad.
Pero la formalidad de la lógica actual convierte la deducción en una inferencia, como consecuencia lógica, en lugar de una implicación con transmisión de contenido en un lenguaje apofántico transmisor de la verdad como pretendía Aristóteles para el lenguaje de la ciencia.
En la nueva forma de relación sintáctica se pierde toda relación de los términos con la gramática del lenguaje y posible "significación". El silogismo pierde así su formalidad de ser categórico, transmisor de la verdad necesaria, "por ser las cosas como son", para adquirir una formalidad hipotética.
Siendo S el sujeto, P el predicado y M el término medio, el silogismo es ahora interpretado como lógica de clases, y su esquema lógico sería del tipo siguiente:
Si la clase S representa la clase como propiedad de ser griego; la clase M representa la clase como propiedad de ser hombre; y la clase P representa la propiedad de ser mortal, entonces el silogismo en Barbara sería:
Si todos los hombres son mortales y todos los griegos son hombres entonces todos los griegos son mortales.
![[(S \subset M) \wedge (M \subset P) \rightarrow (S \subset P)\big]](/images/math/1/e/8/1e89bc6c3094d7a42cd145bc196ee104.png)
Cuando la referencia de instanciación existencial es con respecto a los individuos los juicios aristotélicos pueden formalizarse de la siguiente manera como lógica de predicados:
| Juicio aristotélico | Lógica de predicados |
|---|---|
| Todo S es P | 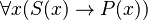 |
| No S es P | 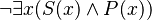 |
| Algún S es P | 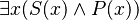 |
| Algún S es no P | 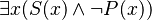 |
El silogismo de esta manera se interpreta como:
Si todos (o algunos) de los individuos que pertenecen (o no pertenecen) al conjunto S (Conjunto Sujeto) pertenecen (o no pertenecen) al conjunto M (Conjunto Término Medio), y todos (o algunos) de los individuos que pertenecen (o no pertenecen) al conjunto M (Conjunto Predicado) pertenecen (o no pertenecen) al conjunto P, entonces todos (o algunos) de los individuos que pertenecen (o no pertenecen) al conjunto S pertenecen (o no pertenecen) al conjunto P.
Y el silogismo en Barbara se formaliza así:
 Siendo M el término Medio, S el sujeto y P el predicado del silogismo.
Siendo M el término Medio, S el sujeto y P el predicado del silogismo.
Si M(x) simboliza "Ser hombre", siendo M=ser hombre lo que se puede predicar respecto a una variable x cuyo compromiso de existencia vendría dado por la cuantificación existencial de la referencia de dicha función, bien sea un cuantificador universal, todo x: 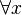 ; un cuantificador particular, algún x:
; un cuantificador particular, algún x: 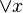 ; o una constante individual determinada: a, b, c…; y P(x) "ser mortal" y M(x) "ser griego", entonces la fórmula
; o una constante individual determinada: a, b, c…; y P(x) "ser mortal" y M(x) "ser griego", entonces la fórmula  representa un silogismo material en barbara. La lógica de predicados resuelve así el problema de la instanciación existencial.
representa un silogismo material en barbara. La lógica de predicados resuelve así el problema de la instanciación existencial.
En ambos casos (como lógica de clases o como lógica de predicados) el silogismo se expresa en fórmulas de relación hipotética; y al no haber afirmación de verdad alguna en las premisas, la conclusión es condicionada y no implicada.
En ambos casos, como relación de clases o como lógica de predicados, el clásico silogismo categórico:
Todos los hombres son mortales. Todos los griegos son hombres. Por tanto todos los griegos son mortales.
Se convierte en un silogismo hipotético:
Si todos los hombres son mortales y todos los griegos son hombres, entonces, todos los griegos son mortales.
Lo que, no cabe duda, es una transformación no menor de la lógica aristotélica.
Juicio de términos
El juicio de términos es la comparación de dos conceptos, bien sea de forma lógica o extraída de la experiencia, mediante la cual creemos o afirmamos la relación de uno con respecto al otro como verdad objetiva. Así se justificaba la creencia verdadera en los juicios aristotélicos de la lógica clásica.
Por ejemplo: en la nieve es blanca, la mente se afirma en que la blancura es una propiedad que se puede predicar con verdad de la nieve. Tal ha sido la consideración de los juicios aristotélicos en el silogismo de la lógica tradicional.
Hoy día la lógica formal y simbólica no acepta tales juicios que se interpretan como creencia, pues no requiere su formulación lingüística o conceptual, como ya consideraron los escolásticos. Por otro lado, la posibilidad de un categórico, como pensaba Aristóteles, está seriamente cuestionada a partir de Kant y su Crítica de la razón pura. Actualmente, en la lógica tal relación se considera formalmente:
- Como resultado de dominio de discurso de la relación de dos clases lógicas.
- Como la atribución de un predicado a una variable lógica individual cuantificada.
Sobre juicio y proposición
Aunque en el silogismo aristotélico se habla de juicio, hoy en día se hablaría de proposición. La diferencia entre juicio y proposición es importante. La proposición afirma un hecho como un todo, que es o no es, como contenido lógico del conocimiento. En cambio, el juicio atribuye un predicado a un sujeto lógico del conocimiento, otorgando a los términos tanto una función lingüística de significado (semántica) como una función formal lógica (sintáctica). Esto influye directamente en el concepto mismo del contenido de un juicios y de una proposición, especialmente en los casos de negación, como se considera más adelante en la lógica silogística.
Mantenemos aquí la denominación de juicio por ser lo más acorde con lo tradicional. Hay que tener en cuenta que este tipo de lógica, como tal, está en desuso, sustituida por la lógica simbólica, en la que la lógica silogística es interpretada como lógica de clases.
Véase también
 En inglés: Syllogism Facts for Kids
En inglés: Syllogism Facts for Kids