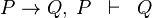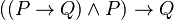Modus ponendo ponens para niños
El modus ponendo ponens (que en latín significa «el modo que, al afirmar, afirma»), también conocido como modus ponens o MP, es una forma de razonamiento lógico muy importante. Es una de las reglas básicas que usamos en la lógica proposicional para sacar conclusiones válidas.
En pocas palabras, el modus ponens funciona así:
- Si sabemos que una cosa (llamémosla P) lleva a otra cosa (llamémosla Q).
- Y también sabemos que esa primera cosa (P) es verdadera.
- Entonces, podemos estar seguros de que la segunda cosa (Q) también es verdadera.
Este tipo de razonamiento se ha usado desde la antigüedad.
El modus ponens se puede representar de forma sencilla:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{cl} & P \to Q \\ & P \\ \hline \therefore & Q \\ \end{array}
Esto significa que si tienes una afirmación como "P implica Q" y también tienes "P" como algo cierto, entonces puedes concluir que "Q" es cierto. Es como si la información de "P" y la conexión "P implica Q" se usaran para "activar" la verdad de "Q".
Un ejemplo claro de modus ponens es:
- Si está lloviendo, te espero dentro del teatro.
- Está lloviendo.
- Por lo tanto, te espero dentro del teatro.
Aunque el modus ponens es muy usado en lógica, no es una ley en sí misma, sino una herramienta. Es uno de los métodos aceptados para construir pruebas lógicas. Permite que, una vez que se usa una afirmación condicional (como "si P, entonces Q") y se confirma su primera parte (P), la segunda parte (Q) pueda seguir adelante en el razonamiento sin tener que repetir todo el "si P, entonces Q". Por eso, a veces se le llama la regla de la separación.
El modus ponens está relacionado con otras formas de razonamiento. Por ejemplo, el modus tollendo tollens es su "opuesto" en cierto sentido. También hay formas de razonamiento que parecen similares pero no son válidas, como la afirmación del consecuente y la negación del antecedente.
Contenido
¿Cómo se escribe formalmente el Modus Ponens?
La regla del modus ponens se puede escribir de varias maneras en lógica formal:
Aquí, el símbolo ⊢ significa que "Q" es una consecuencia lógica de "P → Q" y "P" dentro de un sistema de lógica.
También se puede expresar como una afirmación que siempre es verdadera (una tautología):
En esta expresión, "P" y "Q" representan ideas o afirmaciones que pueden ser verdaderas o falsas.
Entendiendo el Modus Ponens
Este tipo de razonamiento tiene dos partes principales, que llamamos premisas o hipótesis.
- La primera premisa es una afirmación "si-entonces", que dice que si P ocurre, entonces Q ocurrirá.
- La segunda premisa es que P, la primera parte de la afirmación "si-entonces", es realmente cierta.
Si aceptamos estas dos premisas, entonces es necesario que Q, la segunda parte de la afirmación, también sea verdadera. En el campo de la inteligencia artificial, el modus ponens se conoce como "encadenamiento hacia adelante".
Otro ejemplo para entenderlo mejor:
- Si hoy es martes, entonces Juan se irá a trabajar.
- Hoy es martes.
- Por lo tanto, Juan irá a trabajar.
Este argumento es válido, lo que significa que la conclusión se sigue lógicamente de las premisas. Sin embargo, para que un argumento sea "sólido" (es decir, válido y con premisas verdaderas), las premisas deben ser ciertas en la realidad. El ejemplo anterior solo es sólido si realmente es martes y si Juan de verdad va a trabajar los martes.
Relación con el Modus Tollens
El modus ponens y el modus tollendo tollens son dos reglas de inferencia importantes que están conectadas. De hecho, se puede demostrar que una regla se puede derivar de la otra usando otras reglas lógicas.
¿Por qué es válido? La tabla de verdad
Podemos ver por qué el modus ponens es válido usando una tabla de verdad. Una tabla de verdad muestra todas las posibles combinaciones de verdad o falsedad para las afirmaciones "P" y "Q", y cómo esto afecta a la afirmación "P → Q" (P implica Q).
| P | Q | P → Q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | V |
| F | F | V |
En el modus ponens, asumimos que "P → Q" es verdadera y que "P" es verdadera. Si miras la tabla, solo hay una fila donde ambas condiciones se cumplen: la primera fila. En esa fila, "Q" también es verdadera. Esto nos demuestra que siempre que "P → Q" sea verdadera y "P" sea verdadera, "Q" también debe ser verdadera.
Véase también
 En inglés: Modus ponens Facts for Kids
En inglés: Modus ponens Facts for Kids
- Modus tollendo tollens
- Modus tollendo ponens
- Modus ponendo tollens
- Razonamiento deductivo