Elemento de un conjunto para niños
Un elemento o miembro de un conjunto es un objeto que forma parte de ese conjunto. Imagina un conjunto como una colección de cosas. Cada una de esas cosas es un elemento de la colección.
Contenido
¿Qué son los elementos en los conjuntos?
En matemáticas, especialmente en la teoría de conjuntos, usamos los conjuntos para agrupar objetos. Estos objetos pueden ser números, letras, colores o incluso otros conjuntos. Cada objeto dentro de un conjunto se llama elemento.
Por ejemplo, si tenemos el conjunto A formado por los números 1, 2, 3 y 4, escribimos: 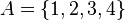 Aquí, los elementos de A son el 1, el 2, el 3 y el 4.
Aquí, los elementos de A son el 1, el 2, el 3 y el 4.
Un grupo de elementos de A, como 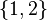 , es un subconjunto de A. Esto significa que todos sus elementos también están en A.
, es un subconjunto de A. Esto significa que todos sus elementos también están en A.
Elementos que son conjuntos
A veces, los elementos de un conjunto pueden ser otros conjuntos. Por ejemplo, mira el conjunto B: 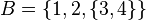 Los elementos de B son el número 1, el número 2 y el conjunto
Los elementos de B son el número 1, el número 2 y el conjunto 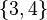 . Es importante notar que el 3 y el 4 no son elementos directos de B, sino que son elementos del conjunto
. Es importante notar que el 3 y el 4 no son elementos directos de B, sino que son elementos del conjunto 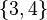 , que a su vez es un elemento de B.
, que a su vez es un elemento de B.
Los elementos de un conjunto pueden ser cualquier cosa que puedas imaginar. Por ejemplo, el conjunto C podría tener colores como elementos: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): C = \{\mathrm{\color{red}rojo}, \mathrm{\color{green}verde}, \mathrm{\color{blue}azul}\} En este caso, los elementos de C son los colores rojo, verde y azul.
¿Cómo se representa la pertenencia de un elemento?
Para mostrar que un objeto es un elemento de un conjunto, usamos un símbolo especial: 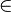 . Este símbolo significa "es un elemento de" o "pertenece a".
. Este símbolo significa "es un elemento de" o "pertenece a".
Cuando escribimos:
Estamos diciendo que  es un elemento del conjunto
es un elemento del conjunto  .
.
Origen del símbolo 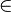
El símbolo 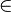 fue usado por primera vez por un matemático llamado Giuseppe Peano en el año 1889. Él lo usó en uno de sus libros importantes. El símbolo se parece a la letra griega epsilon (ε) minúscula, que es la primera letra de la palabra griega "estí", que significa "es".
fue usado por primera vez por un matemático llamado Giuseppe Peano en el año 1889. Él lo usó en uno de sus libros importantes. El símbolo se parece a la letra griega epsilon (ε) minúscula, que es la primera letra de la palabra griega "estí", que significa "es".
Hoy en día, cuando vemos 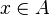 , lo leemos de varias maneras, como:
, lo leemos de varias maneras, como:
- "x es un elemento de A"
- "x es un miembro de A"
- "x pertenece a A"
Diferencia entre pertenencia e inclusión
Es importante no confundir la pertenencia de un elemento con la inclusión de un subconjunto.
- La pertenencia (
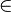 ) se usa para decir que un elemento está dentro de un conjunto.
) se usa para decir que un elemento está dentro de un conjunto. - La inclusión (
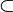 o
o 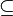 ) se usa para decir que un conjunto está "dentro" de otro conjunto, es decir, que todos sus elementos también pertenecen al otro conjunto.
) se usa para decir que un conjunto está "dentro" de otro conjunto, es decir, que todos sus elementos también pertenecen al otro conjunto.
Aquí tienes una tabla para entenderlo mejor:
| Relación | Símbolo | Se lee |
|---|---|---|
| Pertenencia | 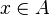 |
x pertenece a A |
| Inclusión | 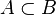 |
A está contenido en B (A es un subconjunto propio de B) |
| Inclusión | 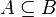 |
A está contenido en B o es igual que B |
¿Qué pasa si un elemento no pertenece?
Si un objeto no es un elemento de un conjunto, usamos el símbolo 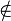 .
.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): x\notin A
Esto significa que  no es un elemento de
no es un elemento de  .
.
¿Cuántos elementos tiene un conjunto?
El número de elementos que tiene un conjunto se llama cardinalidad. Es como decir el "tamaño" de un conjunto.
- Para el conjunto
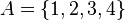 , la cardinalidad es 4, porque tiene 4 elementos.
, la cardinalidad es 4, porque tiene 4 elementos. - Para el conjunto
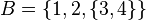 , la cardinalidad es 3, porque tiene 3 elementos (el 1, el 2 y el conjunto
, la cardinalidad es 3, porque tiene 3 elementos (el 1, el 2 y el conjunto 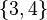 ).
). - Para el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): C = \{\mathrm{\color{red}rojo}, \mathrm{\color{green}verde}, \mathrm{\color{blue}azul}\} , la cardinalidad es 3.
Conjuntos finitos e infinitos
- Un conjunto finito es aquel que tiene un número limitado de elementos, como los ejemplos anteriores. Puedes contarlos todos.
- Un conjunto infinito es aquel que tiene una cantidad ilimitada de elementos. No puedes terminar de contarlos. Un ejemplo es el conjunto de los números naturales, que se representa como
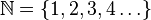 . Los puntos suspensivos indican que la lista continúa para siempre.
. Los puntos suspensivos indican que la lista continúa para siempre.
Ejemplos de elementos en conjuntos
Vamos a usar el conjunto 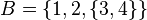 para ver algunos ejemplos:
para ver algunos ejemplos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \in B (El número 2 es un elemento de B).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{3,4\} \in B (El conjunto {3,4} es un elemento de B).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ''amarillo'' \notin B (El color amarillo no es un elemento de B).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 8 \notin B (El número 8 no es un elemento de B).
- La cardinalidad de B, escrita como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): card(B) , es 3.
- La cardinalidad del conjunto {3,4}, escrita como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): card(\{3,4\}) , es 2.
- El conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): D = \{ 2, 4, 6, 8, 10, 12 \} tiene una cardinalidad finita e igual a 6.
- El conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): P = \{ 2, 3, 5, 7, 11, 13... \} (los números primos) tiene una cardinalidad infinita.
Cosas que no podemos decir sobre los elementos
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 2 \subset B (Esto es incorrecto. El 2 es un elemento, no un subconjunto. Para hablar de inclusión, necesitaría ser Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{2\} \subset B ).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3 \in \{3,4\} (Esto es correcto, pero no se refiere a la relación con el conjunto B. El 3 es un elemento del conjunto {3,4}, que a su vez es un elemento de B).
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B \in B (Un conjunto no es un elemento de sí mismo. Un conjunto puede ser un subconjunto de sí mismo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B \subseteq B , pero no un elemento).
Galería de imágenes
-
Primera utilización del símbolo
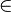 por Giuseppe Peano
por Giuseppe Peano -
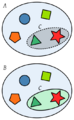
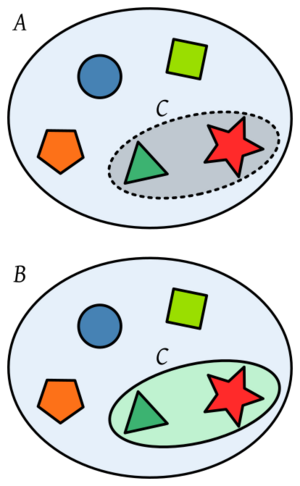
Diferencia entre elemento y subconjunto. El conjunto C está formado por dos elementos. El conjunto A está formado por cinco elementos (cinco figuras geométricas), y C, señalado con línea discontinua, es un subconjunto de A, C ⊆ A. El conjunto B, por el contrario, está formado por cuatro elementos: tres figuras geométricas y un conjunto, a saber, C. Por tanto, C, señalado con línea continua, es un elemento de B, C ∈ B.