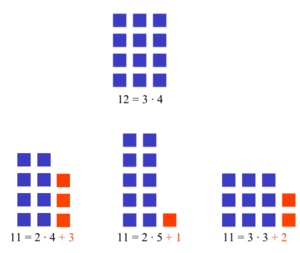Número primo para niños
En matemáticas, un número primo es un número natural especial. Es un número mayor que 1 que solo puede dividirse de forma exacta entre dos números: el 1 y él mismo. Por ejemplo, el 7 es un número primo porque solo se puede dividir entre 1 y 7.
Los números que no son primos (y son mayores que 1) se llaman números compuestos. Estos números tienen más de dos divisores. Por ejemplo, el 6 es compuesto porque se puede dividir entre 1, 2, 3 y 6. El número 1 es un caso especial; no se considera ni primo ni compuesto.
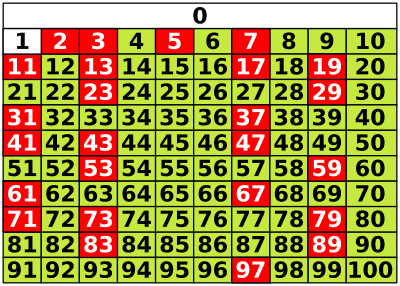
Los primeros números primos son: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
La cualidad de ser un número primo se llama primalidad. El estudio de estos números es una parte muy importante de la teoría de números, una rama de las matemáticas.
Contenido
Historia de los Números Primos
¿Cuándo se descubrieron los números primos?
Se cree que la gente ya conocía los números primos hace mucho tiempo. El hueso de Ishango, una herramienta antigua de hace más de 20.000 años, tiene marcas que algunos expertos interpretan como una señal de que se conocían los números 11, 13, 17 y 19.
Las civilizaciones antiguas como los babilonios y los egipcios también usaban conceptos relacionados con los números primos en sus cálculos. Por ejemplo, los babilonios necesitaban entender la multiplicación y la división. Los egipcios usaban fracciones especiales que requerían conocimientos de divisores.
¿Quién fue Euclides y qué hizo por los números primos?
La primera vez que se escribió claramente sobre los números primos fue hace unos 300 años antes de Cristo. Fue en la obra Elementos del matemático Euclides. Él definió los números primos y demostró que hay una cantidad infinita de ellos. También explicó cómo encontrar el máximo común divisor y el mínimo común múltiplo.
La criba de Eratóstenes es un método sencillo para encontrar números primos. Se le atribuye a Eratóstenes de Cirene, otro matemático griego. Aunque hoy en día se usan métodos más avanzados para encontrar números primos muy grandes con computadoras.
¿Qué pasó con los números primos después de los griegos?
Después de la Antigua Grecia, el estudio de los números primos no avanzó mucho hasta el siglo XVII. En 1640, Pierre de Fermat propuso un teorema importante sobre los números primos. Él también pensó que todos los números de una forma especial (llamados números de Fermat) eran primos, pero más tarde se descubrió que no siempre era así.
Otro matemático, Marin Mersenne, estudió los números primos de otra forma especial, que ahora se conocen como números de Mersenne.
En el siglo XVIII, Leonhard Euler hizo muchos descubrimientos sobre los números primos. Demostró que la suma de los inversos de los números primos (1/2 + 1/3 + 1/5 + ...) es infinita.
Más tarde, en el siglo XIX, Gauss y Legendre predijeron cómo se distribuyen los números primos. Esta idea llevó al teorema de los números primos, que fue demostrado en 1896 por Hadamard y De la Vallée-Poussin.
En los años 70, los números primos se volvieron muy importantes para la criptografía de clave pública. Esto es una forma de enviar mensajes secretos de manera segura. El algoritmo RSA, por ejemplo, usa números primos muy grandes.
Desde 1951, los números primos más grandes se han descubierto con la ayuda de computadoras. Proyectos como GIMPS (Great Internet Mersenne Prime Search) usan miles de computadoras para buscar nuevos números primos.
Propiedades de los Números Primos
¿Por qué el número 1 no es primo?
Hasta el siglo XIX, algunos matemáticos consideraban el 1 como un número primo. Sin embargo, hoy en día, la mayoría de los matemáticos no lo hacen. Esto se debe a que si el 1 fuera primo, el teorema fundamental de la aritmética sería más complicado. Este teorema dice que cualquier número natural se puede escribir de una única manera como producto de números primos. Si el 1 fuera primo, podríamos añadirlo cuantas veces quisiéramos a la multiplicación, y la unicidad se perdería.
¿Qué es el Teorema Fundamental de la Aritmética?
El teorema fundamental de la aritmética es muy importante. Dice que cada número natural (mayor que 1) se puede formar multiplicando números primos. Piensa en los números primos como los "ladrillos" básicos con los que se construyen todos los demás números. Por ejemplo, el número 12 se puede escribir como 2 × 2 × 3. No hay otra forma de escribir 12 usando solo números primos.
Este teorema nos ayuda a entender otros conceptos matemáticos:
- El mínimo común múltiplo (m.c.m.) de dos o más números es el número más pequeño que es múltiplo de todos ellos. Para calcularlo, se usan los factores primos de cada número.
- El máximo común divisor (m.c.d.) de dos o más números es el número más grande que los divide a todos. También se calcula con los factores primos.
- Dos números son coprimos si su máximo común divisor es 1. Esto significa que no comparten ningún factor primo.
Otras características de los números primos
- Todos los números primos, excepto el 2 y el 5, terminan en 1, 3, 7 o 9.
- Todos los números primos, excepto el 2 y el 3, se pueden escribir como 6 veces un número más 1, o 6 veces un número menos 1.
- El pequeño teorema de Fermat dice que si p es un número primo, y a es cualquier número natural, entonces a elevado a p menos a es divisible por p.
El Conjunto de los Números Primos
¿Hay infinitos números primos?
Sí, hay infinitos números primos. Euclides lo demostró hace mucho tiempo. Su idea es sencilla: Imagina que solo hay una cantidad finita de números primos. Podríamos multiplicarlos todos y sumar 1 al resultado. Este nuevo número no sería divisible por ninguno de los primos de nuestra lista. Entonces, este nuevo número debe ser primo o tener un factor primo que no estaba en nuestra lista. En cualquier caso, ¡encontramos un nuevo primo! Esto significa que nuestra lista original no era completa, y siempre podemos encontrar más.
¿Con qué frecuencia aparecen los números primos?
 |
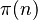 |
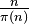 |
|---|---|---|
| 10 | 4 | 2,500 |
| 102 | 25 | 4,000 |
| 103 | 168 | 5,952 |
| 104 | 1.229 | 8,137 |
| 105 | 9.592 | 10,425 |
| 106 | 78.498 | 12,740 |
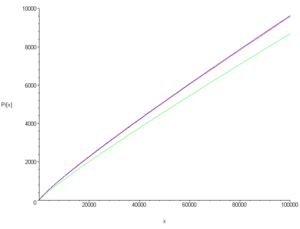
Aunque hay infinitos números primos, no aparecen de forma regular. Al principio, están muy juntos (2, 3, 5, 7). Pero a medida que los números se hacen más grandes, los primos se vuelven más escasos.
Los matemáticos han estudiado cómo se distribuyen los primos. La función π(n) cuenta cuántos números primos hay hasta un número n. El teorema de los números primos nos da una idea de cuántos primos esperar encontrar. Dice que la cantidad de primos hasta n es aproximadamente n dividido por el logaritmo natural de n.
¿Qué tan grandes pueden ser los espacios entre primos?
La diferencia entre dos números primos consecutivos puede ser tan pequeña como 2 (como entre 3 y 5, o 11 y 13). A estos se les llama primos gemelos. Pero también puede ser tan grande como queramos. Podemos encontrar secuencias de números compuestos (no primos) tan largas como deseemos.
Por ejemplo, si queremos un espacio de cinco números compuestos, podemos usar los números después de 6! (factorial de 6, que es 720):
- 722 (es divisible por 2)
- 723 (es divisible por 3)
- 724 (es divisible por 4)
- 725 (es divisible por 5)
- 726 (es divisible por 6)
Todos estos son números compuestos. El siguiente, 727, es primo.
Encontrar Números Primos
¿Cómo se sabe si un número es primo?

Para saber si un número es primo, se usan los tests de primalidad.
- La criba de Eratóstenes es un método antiguo para encontrar todos los primos hasta un número específico. Consiste en hacer una lista de números y tachar los múltiplos de los primos que ya se han encontrado.
- Para un número grande, se usa la división por tentativa. Se divide el número entre todos los primos más pequeños que su raíz cuadrada. Si ninguna división es exacta, el número es primo. Si alguna división es exacta, el número es compuesto. Este método es lento para números muy grandes.
Para números enormes (de miles de cifras), se usan algoritmos más avanzados y rápidos. Algunos de estos tests son "probabilísticos", lo que significa que dan una respuesta con una alta probabilidad de ser correcta, pero no 100% segura. Otros son "determinísticos", que siempre dan una respuesta segura.
¿Qué son los algoritmos de factorización?
Un algoritmo de factorización es un método para encontrar los factores primos de un número. Es decir, para descomponer un número en sus "ladrillos" primos. La seguridad de muchos sistemas de cifrado (como el algoritmo RSA) se basa en que es muy difícil y lento factorizar números muy grandes.
¿Existen fórmulas para generar números primos?
Los matemáticos han buscado fórmulas que solo generen números primos. Aunque se han encontrado algunas, no son prácticas. Por ejemplo, hay polinomios con muchas variables que, al darles ciertos valores, producen números primos. Pero estos polinomios también producen muchos números negativos o compuestos, y son muy difíciles de calcular.
Clases de Números Primos Especiales
Hay muchos tipos de números primos que tienen nombres especiales porque cumplen ciertas condiciones o se generan con fórmulas específicas.
Primos de Fermat
Los números de Fermat son de la forma 2 elevado a (2 elevado a n) más 1. Solo se conocen cinco números primos de Fermat, que corresponden a n = 0, 1, 2, 3 y 4. Los demás números de Fermat que se han estudiado son compuestos.
Primos de Mersenne
Los números de Mersenne son de la forma 2 elevado a p menos 1, donde p es un número primo. Los números primos más grandes que se conocen suelen ser de este tipo. Esto es porque hay un test muy eficiente para comprobar si un número de Mersenne es primo.
El número primo más grande conocido hasta ahora es un número de Mersenne: 2136.279.841 - 1. ¡Tiene más de 41 millones de cifras! Fue descubierto en 2024 gracias al proyecto GIMPS.
Otros tipos de primos
- Números primos gemelos: Son pares de primos que se diferencian en 2, como (3,5) o (11,13).
- Número primo de Sophie Germain: Un primo p es de Sophie Germain si 2p + 1 también es primo.
- Omirp: Son primos que, al invertir el orden de sus cifras, también resultan ser primos (por ejemplo, 13 y 31).
- Palindrómicos: Son primos que se leen igual de izquierda a derecha que de derecha a izquierda (por ejemplo, 101).
Conjeturas sobre Números Primos
Una conjetura es una afirmación matemática que se cree que es cierta, pero que aún no se ha demostrado. Hay muchas conjeturas sobre los números primos.
La Hipótesis de Riemann
La hipótesis de Riemann es una de las conjeturas más famosas y difíciles de las matemáticas. Propuesta en 1859, aún no se ha resuelto. Si fuera cierta, nos daría mucha información sobre cómo se distribuyen los números primos. En pocas palabras, sugiere que los números primos están distribuidos de la manera más "regular" posible, sin grandes sorpresas.
Otras conjeturas importantes
- La conjetura de los números primos gemelos dice que hay infinitos pares de primos gemelos.
- La conjetura de Goldbach dice que todo número par mayor que 2 se puede escribir como la suma de dos números primos (por ejemplo, 4 = 2+2, 6 = 3+3, 8 = 3+5). Hay una versión más débil que dice que todo número impar mayor que 5 se puede escribir como suma de tres primos.
Aplicaciones de los Números Primos
En la computación y la seguridad
Los números primos son fundamentales en la criptografía moderna, que es el arte de escribir y descifrar mensajes secretos. El algoritmo RSA, por ejemplo, usa dos números primos muy grandes para crear una clave pública. La seguridad de este sistema se basa en que es extremadamente difícil encontrar los factores primos de un número muy grande.
En el arte y la literatura
Los números primos han fascinado a muchas personas, incluyendo artistas y escritores:
- El compositor Olivier Messiaen usó duraciones de notas basadas en números primos para crear ritmos únicos en su música.
- En la novela Contact de Carl Sagan, se sugiere que los números primos podrían ser una forma de comunicarse con vida extraterrestre.
- La novela El curioso incidente del perro a medianoche numera sus capítulos solo con números primos.
- La soledad de los números primos es una novela famosa que ganó un premio importante.
- Películas como Una mente maravillosa y El tío Petros y la conjetura de Goldbach también exploran el mundo de las matemáticas y los números primos.
Véase también
 En inglés: Prime number Facts for Kids
En inglés: Prime number Facts for Kids