Henri Poincaré para niños
Jules Henri Poincaré (Nancy, Francia, 29 de abril de 1854-París, 17 de julio de 1912), conocido como Henri Poincaré, fue un brillante matemático, físico y filósofo de la ciencia francés. Era primo de Raymond Poincaré, quien llegó a ser presidente de Francia. Se le considera uno de los últimos grandes científicos que dominó y contribuyó en casi todas las áreas de las matemáticas de su tiempo. En 1894, estableció el concepto de grupo fundamental en topología, una rama de las matemáticas.
Datos para niños Henri Poincaré |
||
|---|---|---|
 Jules Henri Poincaré (1854-1912). Foto en el frontispicio de la edición 1913 de Dernières pensées (Sobre la ciencia y su método: el espacio, últimos pensamientos).
|
||
| Información personal | ||
| Nombre de nacimiento | Jules Henri Poincaré | |
| Nacimiento | 29 de abril de 1854 Nancy, Meurthe-et-Moselle |
|
| Fallecimiento | 17 de julio de 1912 París, Francia |
|
| Causa de muerte | Émbolo | |
| Sepultura | Cementerio de Montparnasse | |
| Residencia | Francia | |
| Nacionalidad | Francia | |
| Religión | Católico (hasta 1872) | |
| Lengua materna | Francés | |
| Familia | ||
| Padres | León Poincaré (1828-1892) Eugénie Launois (1830-1897) |
|
| Cónyuge | Jeanne-Louise Poulain d'Annecy | |
| Educación | ||
| Educación | doctor en Filosofía | |
| Educado en | Lycée Nancy École Polytechnique École des Mines |
|
| Supervisor doctoral | Charles Hermite | |
| Alumno de | Charles Hermite | |
| Información profesional | ||
| Área | Matemática, Física, Estadística | |
| Conocido por | Conjetura de Poincaré Problema de los tres cuerpos Topología Relatividad especial Teorema de Poincaré-Hopf Dualidad de Poincaré Teorema di Poincaré-Birkhoff-Witt Desigualdad de Poincaré Series Hilbert–Poincaré Tensor de Poincaré Número rotacional Acuñó el término 'número de Betti' Teoría del Caos Universo Esfera Teorema de Poincaré-Bendixson Método de Poincaré–Lindstedt Teorema de recurrencia |
|
| Cargos ocupados |
|
|
| Empleador | Corps des Mines Universidad de Caen La Sorbonne Bureau des Longitudes |
|
| Estudiantes doctorales | Louis Bachelier Dimitrie Pompeiu Mihailo Petrović |
|
| Alumnos | Dimitrie Pompeiu y Louis Bachelier | |
| Obras notables | Ciencias e Hipótesis | |
| Conflictos | Guerra franco-prusiana | |
| Miembro de |
|
|
| Distinciones | Medalla de oro RAS en 1900 Medalla Sylvester en 1901 Medalla Matteucci en 1905 Medalla Bruce en 1911 |
|
| Firma | ||
 |
||
Contenido
¿Quién fue Henri Poincaré?
Jules Henri Poincaré nació el 29 de abril de 1854 en Nancy, Francia. Provenía de una familia importante. Su padre, León Poincaré, era profesor de medicina. Su primo, Raymond Poincaré, llegó a ser presidente de Francia.
Sus Primeros Años y Estudios
Cuando era niño, Henri tuvo una enfermedad llamada difteria. Por eso, su madre, Eugénie Launois, que era muy inteligente, lo educó en casa. Henri era muy bueno escribiendo.
En 1862, entró al Liceo de Nancy, que hoy lleva su nombre. Durante once años, fue uno de los mejores estudiantes en casi todas las materias. Su profesor de matemáticas lo llamó "un monstruo de las matemáticas". Ganó muchos premios en concursos nacionales para estudiantes destacados. Las únicas materias en las que no era tan bueno eran música y educación física. Algunos creen que esto se debía a problemas de visión y a que se distraía fácilmente. Se graduó en 1871.
En 1873, ingresó a la famosa École Polytechnique. Allí estudió matemáticas con Charles Hermite. Publicó su primer artículo científico en 1874. Después, continuó sus estudios en la École des Mines, donde se graduó como ingeniero en 1879.
Como ingeniero, Poincaré trabajó en el Corps des Mines. Incluso investigó un accidente en una mina en 1879, donde 18 mineros perdieron la vida. Al mismo tiempo, preparaba su doctorado en matemáticas. Su tesis trataba sobre las ecuaciones diferenciales. Poincaré inventó una nueva forma de estudiar estas ecuaciones. Fue el primero en ver cómo sus propiedades geométricas podían ayudar a entender el movimiento de cuerpos en el Sistema Solar. Obtuvo su doctorado en la Universidad de París en 1879.
Grandes Descubrimientos de Poincaré
Después de graduarse, Poincaré fue profesor en la Universidad de Caen. Aunque se dedicó a las matemáticas, nunca dejó del todo su trabajo en minería. También trabajó en el Ministerio de Servicios Públicos, ayudando en el desarrollo de ferrocarriles.
Desde 1881, fue profesor en la Universidad de París (La Sorbona). Allí enseñó varias materias, como Mecánica Física, Física Matemática y Astronomía. En 1881, se casó con Louise Poulain d'Andecy y tuvieron cuatro hijos.
El Problema de los Tres Cuerpos
En 1884, el rey Óscar II de Suecia y Noruega organizó un concurso de matemáticas. Uno de los problemas era sobre la estabilidad del Sistema Solar, conocido como el problema de n cuerpos. Poincaré decidió participar. Se enfocó en una versión más sencilla, el problema de los tres cuerpos. Su trabajo fue tan bueno que ganó el concurso en 1889.
Poincaré descubrió que el movimiento de sistemas como este puede ser muy impredecible. Una pequeña diferencia al principio puede llevar a resultados muy distintos más adelante. Esto significa que es difícil predecir el futuro de estos sistemas con exactitud. Su trabajo fue tan importante que se considera el inicio de la teoría del Caos.
Contribuciones a la Relatividad
Poincaré hizo contribuciones importantes a la teoría de la relatividad. En 1893, trabajó en el Bureau des Longitudes de Francia, donde ayudó a sincronizar los horarios del mundo. Esto lo llevó a pensar en cómo se sincronizan los relojes que se mueven.

Él estudió las ideas de otros científicos y llegó a muchas conclusiones que hoy se asocian con la Teoría de la Relatividad Especial. Por ejemplo, habló sobre la dificultad de saber si dos eventos lejanos ocurren al mismo tiempo. También formuló el Principio de relatividad, que dice que ningún experimento puede diferenciar entre un movimiento uniforme y el reposo.
En 1900, Poincaré analizó cómo la emisión de radiación de un objeto afectaba su masa. Su resultado era similar a la famosa ecuación de Einstein, 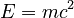 , aunque con un significado físico diferente en ese momento. A pesar de sus aportes, Poincaré siguió creyendo en el concepto del éter después de que Einstein publicara su teoría de la relatividad en 1905.
, aunque con un significado físico diferente en ese momento. A pesar de sus aportes, Poincaré siguió creyendo en el concepto del éter después de que Einstein publicara su teoría de la relatividad en 1905.
Últimos Años y la Conjetura de Poincaré
En sus últimos años, Poincaré trabajó en una teoría de la gravedad que fue un paso previo a la relatividad general. Incluso mencionó las "ondas de gravedad".
También es famoso por plantear uno de los problemas más conocidos en matemáticas: la conjetura de Poincaré. Este problema de Topología, propuesto en 1904, fue resuelto por el matemático ruso Grigori Perelmán en 2002. Por resolverlo, Perelmán recibió el Premio del Milenio.
En 1899 y 1904, Poincaré participó en los juicios de Alfred Dreyfus. Ayudó a demostrar que algunas pruebas científicas presentadas contra Dreyfus, un oficial del ejército, eran incorrectas.
En 1887, a los 32 años, Poincaré fue elegido miembro de la Academia de Ciencias Francesa. En 1906, fue presidente de esta academia, y en 1909, miembro de la Academia Francesa.
Henri Poincaré falleció el 17 de julio de 1912, a los 58 años, debido a una complicación de salud. Está enterrado en el Cementerio de Montparnasse en París.
Su Forma de Trabajar
Poincaré era muy curioso sobre cómo funcionaba su propia mente. Incluso dio una charla en 1908 sobre sus observaciones. Se decía que trabajaba como una abeja, moviéndose de un tema a otro.
El matemático Darboux lo describió como "intuitivo" porque a menudo pensaba con imágenes. A Poincaré no le gustaba ser demasiado estricto en sus métodos. Creía que la lógica era buena para organizar ideas, pero que podía limitar la creatividad.
Cómo era su rutina
Un psicólogo llamado Édouard Toulouse estudió la rutina diaria de Poincaré. Poincaré trabajaba a las mismas horas cada día, pero por períodos cortos. Dedicaba unas cuatro horas al día a la investigación matemática. Tenía una memoria increíble y podía recordar la página y la línea de cualquier texto que hubiera leído. También recordaba lo que le decían palabra por palabra.
Su forma de trabajar era resolver los problemas en su mente y luego escribir la solución. Poincaré era ambidiestro (usaba ambas manos) y tenía hipermetropía (dificultad para ver de cerca). Su habilidad para visualizar lo que escuchaba le ayudó mucho en clase, ya que su mala vista le impedía ver lo que los profesores escribían en la pizarra.
A pesar de sus muchas virtudes, Poincaré no era muy bueno en educación física ni en arte. Siempre tenía prisa y no le gustaba volver atrás para corregir cosas. No pasaba mucho tiempo en un solo problema, porque creía que su mente seguiría trabajando en él mientras él se dedicaba a otra cosa.
Contribuciones Importantes
Poincaré hizo muchas contribuciones en áreas como:
- Topología algebraica (el estudio de las formas y espacios).
- Teoría de funciones complejas.
- Geometría algebraica.
- Teoría de números.
- Problema de los tres cuerpos.
- Electromagnetismo.
- Teoría de la Relatividad Especial.
- Introdujo el concepto de grupo fundamental en 1894.
- Hizo aportes clave a las ecuaciones diferenciales, como la Esfera de Poincaré.
También contribuyó en Mecánica celeste, Mecánica de fluidos, Óptica, Electricidad, termodinámica y cosmología.
Además, fue un gran divulgador de la ciencia. Escribió varios libros para el público en general, explicando que la creación matemática a menudo ocurría en el subconsciente antes de que la solución apareciera en la mente consciente.
Honores y Reconocimientos
Premios
- Ganó el concurso matemático del Rey Óscar II en 1889.
- Recibió la Medalla de oro de la Real Sociedad Astronómica de Londres en 1900.
- Ganó la Medalla Bruce en 1911.
Lugares y Objetos con su Nombre
Henri Poincaré nunca recibió el Premio Nobel de Física, aunque fue nominado muchas veces. Algunos miembros del comité del Nobel consideraban que sus trabajos eran más teóricos que experimentales, y no siempre comprendían la magnitud de los problemas que abordaba.
Obras Destacadas
Algunas Publicaciones
Su principal contribución a la topología algebraica fue Analysis situs (1895), el primer estudio sistemático de la topología.
También publicó dos obras fundamentales sobre la mecánica celestial:
- Leçons de mécanique céleste. (1905-10).
Escribió libros para el público general para explicar la ciencia:
- La Science et l'hypothèse (1902).
- La Valeur de la science (1904).
- Science et méthode (1908).
- Dernières pensées (1913).
Véase también
 En inglés: Henri Poincaré Facts for Kids
En inglés: Henri Poincaré Facts for Kids
- Conjetura de Poincaré
- Grupo de Poincaré
- Topología
- Teoría del Caos


