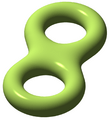Grupo fundamental para niños
En topología, que es una rama de las matemáticas que estudia las formas y los espacios, podemos usar una herramienta especial llamada grupo fundamental. Este grupo nos ayuda a entender cómo son los "agujeros" o las "curvas" en un espacio. Imagina que tienes una superficie, como una dona o una pelota. El grupo fundamental nos dice cuántos tipos diferentes de lazos (caminos cerrados) puedes dibujar en esa superficie sin que se rompan.
Este grupo se asocia a un punto específico del espacio, llamado punto base. Los elementos del grupo fundamental son "clases de equivalencia" de lazos. Esto significa que agrupamos los lazos que se pueden transformar uno en otro sin romperse.
El grupo fundamental también se conoce como el primer grupo de homotopía. Se escribe a menudo como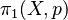 
, donde 
es el espacio y 
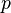es el punto base.
Contenido
¿Qué es el Grupo Fundamental?
El grupo fundamental es una forma de describir las características de un espacio, especialmente sus "agujeros" o "burbujas". Piensa en ello como una huella digital matemática de la forma de un objeto.
Entendiendo el Grupo Fundamental
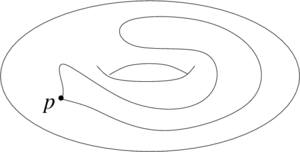
Para entenderlo, imagina que estás en un espacio, como una superficie. Eliges un punto de partida. Luego, dibujas un camino que empieza en ese punto, da algunas vueltas y regresa al mismo punto. A este camino lo llamamos un lazo o bucle.
Lazos y Caminos Cerrados
Un lazo es como un hilo elástico que estiras y luego lo unes a su punto de inicio. Puedes tener muchos lazos diferentes en el mismo espacio.
¿Cuándo son Equivalentes los Lazos?
Dos lazos se consideran "equivalentes" si puedes transformar uno en el otro de forma continua, sin romperlo ni salirte del espacio. Imagina que los lazos son de goma. Si puedes estirar, encoger o mover un lazo hasta que se vea exactamente como otro, entonces son equivalentes.
El grupo fundamental se forma al agrupar todos los lazos equivalentes. Luego, podemos "combinar" lazos: primero recorres un lazo y luego el otro. Esta combinación nos da una forma de "multiplicar" los elementos del grupo.
Un Poco de Historia
El concepto del grupo fundamental fue introducido por el matemático francés Henri Poincaré en 1895. Surgió de estudios sobre superficies y funciones complejas, ayudando a clasificar diferentes tipos de superficies.
Ejemplos Sencillos del Grupo Fundamental
El grupo fundamental nos ayuda a distinguir entre diferentes formas. Aquí tienes algunos ejemplos:
Espacios sin "Agujeros"
Algunos espacios no tienen "agujeros" que puedas rodear. Por ejemplo, una pelota de fútbol o un cubo. En estos espacios, cualquier lazo que dibujes puede encogerse hasta convertirse en un solo punto. Decimos que su grupo fundamental es "trivial" o que son simplemente conexos. Esto significa que no hay lazos interesantes que no se puedan deshacer.
La Circunferencia: Un Ejemplo Clásico
La circunferencia (un círculo) es un ejemplo interesante. Si dibujas un lazo en una circunferencia, puedes darle una vuelta, dos vueltas, o incluso ir en sentido contrario. El grupo fundamental de la circunferencia es como los números enteros (..., -2, -1, 0, 1, 2, ...). Cada número representa cuántas vueltas completas da el lazo alrededor de la circunferencia y en qué dirección.
El Toro: Más de un "Agujero"
Un toro es como una dona. Tiene dos tipos de "agujeros" principales. Puedes rodear el agujero central (como si pasaras el lazo por el centro de la dona) o puedes rodear la "barriga" de la dona. El grupo fundamental de un toro es más complejo, porque puedes combinar estos dos tipos de vueltas.
Cuando el Orden Importa: Grupos No Conmutativos
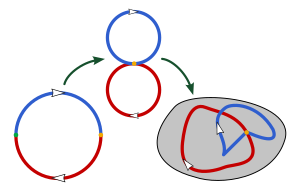
A veces, el orden en que combinas los lazos sí importa. Por ejemplo, si tienes un plano con dos puntos quitados, el grupo fundamental no es "conmutativo". Esto significa que si primero rodeas un punto y luego el otro, el resultado puede ser diferente a si lo haces al revés.
Dependencia del Punto Base
Aunque el grupo fundamental se define con un punto base, si el espacio está "conectado por caminos" (es decir, puedes ir de cualquier punto a cualquier otro punto con un camino), entonces la elección del punto base no cambia la "forma" del grupo. Los grupos resultantes son "isomorfos", lo que significa que son matemáticamente equivalentes. Por eso, a menudo se escribe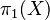 
sin especificar el punto base.
Galería de imágenes
-
Mediante lazos con base en un punto fijo podemos explorar el espacio topológico al que pertenece. Las clases de equivalencia de estos lazos formarán el grupo fundamental.
-
Un ejemplo típico de espacio topológico es una superficie como la representada a la derecha.
-
Producto de lazos.
Véase también
En inglés: Fundamental group Facts for Kids
