Número algebraico para niños
Un número algebraico es un tipo especial de número, ya sea real o complejo, que se puede encontrar como la solución de una ecuación polinómica. Una ecuación polinómica es una expresión matemática que se ve así:
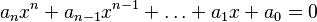
En esta ecuación:
- `n` es un número entero positivo que indica el grado más alto del polinomio.
- Los números `a_0, a_1, ..., a_n` se llaman coeficientes, y deben ser números racionales (es decir, pueden escribirse como una fracción).
- El coeficiente `a_n` no puede ser cero.
En resumen, si un número es la "respuesta" a una ecuación de este tipo, donde todos los números que lo acompañan son fracciones, entonces es un número algebraico.
Contenido
Ejemplos de Números Algebraicos
Para entender mejor, veamos algunos ejemplos de números que son algebraicos y otros que no lo son.
Números Racionales
Todos los números racionales son algebraicos. Un número racional es una fracción como 1/2 o 3/4. Por ejemplo, la fracción 2/3 es la solución de la ecuación `3x - 2 = 0`. Como esta es una ecuación polinómica con coeficientes racionales (3 y -2), 2/3 es un número algebraico.
Números Irracionales Algebraicos
Algunos números irracionales también son algebraicos. Los números irracionales son aquellos que no se pueden escribir como una fracción, como la raíz cuadrada de 2.
- La raíz cuadrada de 2 (
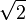) es un número algebraico porque es la solución de la ecuación `x^2 - 2 = 0`. - Otro ejemplo es
![\frac{\sqrt[3]{3}}{2}](/images/math/e/3/3/e3389d2b832b1ea8973ec2c8cfb5bac0.png)
, que es la solución de la ecuación `8x^3 - 3 = 0`.
Números Imaginarios Algebraicos
El número imaginario `i` (que es la raíz cuadrada de -1) también es algebraico. Es la solución de la ecuación `x^2 + 1 = 0`.
Números Trascendentes (No Algebraicos)
Existen otros números irracionales que no son algebraicos. A estos se les llama números trascendentes.
- El número
(pi), que usamos para calcular la circunferencia de un círculo, es un número trascendente. Esto fue demostrado por el matemático Ferdinand von Lindemann en 1882. - El número `e` (la base de los logaritmos naturales) también es trascendente, demostrado por Charles Hermite en 1873.
Características de los Números Algebraicos
¿Qué es el Grado de un Número Algebraico?
El grado de un número algebraico es el grado más pequeño de la ecuación polinómica con coeficientes racionales de la que es solución.
- Por ejemplo, los números racionales son números algebraicos de grado uno. Esto se debe a que siempre podemos encontrar una ecuación de primer grado (como `qx - p = 0`) que los tenga como solución.
- El número
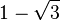es de grado dos. Es la solución de una ecuación de segundo grado, pero no de una de primer grado. - El número
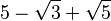es de grado cuatro. Es la solución de una ecuación de cuarto grado, pero no de una de tercer grado.
Propiedades del Conjunto de los Números Algebraicos
Los números algebraicos tienen propiedades interesantes:
- Si sumas, restas, multiplicas o divides dos números algebraicos (excepto dividir por cero), el resultado siempre será otro número algebraico. Esto significa que forman un "cuerpo matemático", un conjunto donde estas operaciones se pueden realizar y el resultado siempre se mantiene dentro del mismo conjunto.
- Por ejemplo, si sumas un número racional y una raíz (como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{2}{5} + \sqrt[3]{7} ), el resultado es un número algebraico.
- Todos los números que se pueden formar usando números racionales y las operaciones básicas (suma, resta, multiplicación, división, potencias y raíces) son números algebraicos.
- El conjunto de todos los números algebraicos es "contable". Esto significa que, aunque hay infinitos números algebraicos, se pueden poner en una lista, como los números naturales (1, 2, 3...).
Enteros Algebraicos
Un entero algebraico es un tipo especial de número algebraico. Es aquel que es solución de una ecuación polinómica donde el coeficiente principal (`a_n`) es 1, y todos los demás coeficientes son números enteros.
- Algunos ejemplos son
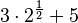o 
. - Si sumas, restas o multiplicas dos enteros algebraicos, el resultado también será un entero algebraico.
- Los únicos números racionales que son enteros algebraicos son los propios números enteros.
Historia de los Números Algebraicos
El matemático Leonhard Euler fue quien, en 1748, empezó a clasificar los números en "algebraicos" y "trascendentes". Más tarde, en 1844, el matemático Liouville encontró una manera de saber si un número era trascendente. La teoría más completa sobre los números algebraicos fue desarrollada por matemáticos como Dedekind y Yegor Zolotariov a finales del siglo XIX, basándose en trabajos anteriores de Kummer.
Galería de imágenes
-
Números algebraicos del plano complejo coloreados con azul, cyan, rojo y verde según su grado 4, 3, 2 y 1 respectivamente. La circunferencia unitaria en color negro.
Véase también
En inglés: Algebraic number Facts for Kids
