Grafo completo para niños
Datos para niños Grafo completo |
||
|---|---|---|
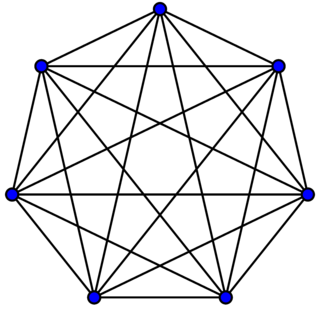 K7, grafo completo de 7 vértices.
|
||
| Vértices | n | |
| Aristas | n (n-1)/2 | |
| Diámetro | 1 | |
| Cintura | 3, si n ≥ 3 | |
| Automorfismos | n! (Sn) | |
| Número cromático | n | |
| Índice cromático | n, si n es impar n-1, si n es par |
|
| Propiedades | (n-1)-regular Simétrico Vértice transitivo Arista transitivo Distancia unidad Fuertemente regular Integral |
|
En el mundo de las matemáticas, un grafo completo es un tipo especial de grafo simple. Imagina un grupo de amigos donde cada persona está conectada directamente con todas las demás. Eso es un grafo completo.
En un grafo completo, cada uno de sus puntos (llamados vértices) está unido a todos los demás puntos por una línea (llamada arista). Si un grafo tiene n vértices, el número de aristas se puede calcular con la fórmula 
.
Los grafos completos se representan con la letra K seguida de un número, por ejemplo,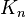 
. Son grafos regulares, lo que significa que todos sus vértices tienen el mismo número de conexiones. Cada vértice en un grafo completo de n vértices tiene 
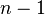conexiones.
Para que un grafo completo se separe en partes, tendrías que quitar todos sus vértices. Esto demuestra lo fuertemente conectados que están.
¿Qué es un grafo plano?
Un grafo plano es un tipo de grafo que se puede dibujar en una superficie plana (como una hoja de papel) sin que ninguna de sus líneas se cruce. Es como dibujar un mapa sin que los caminos se superpongan.
El teorema de Kuratowski nos dice algo interesante sobre los grafos completos. Explica que un grafo plano no puede contener un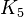 
(un grafo completo con 5 vértices) ni un grafo bipartito completo 
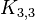. Esto significa que si intentas dibujar un grafo completo con 5 o más vértices, siempre habrá líneas que se crucen.
Ejemplos de grafos completos
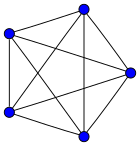
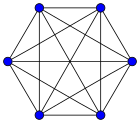
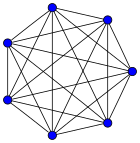
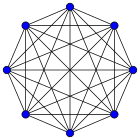
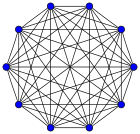
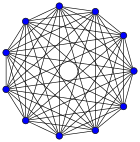
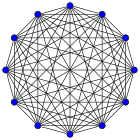
Aquí puedes ver cómo se ven los grafos completos con diferentes números de vértices, desde 1 hasta 12. El número junto a la K indica cuántos vértices tiene el grafo, y el número después de los dos puntos es la cantidad de aristas (líneas) que lo conectan.
| K1: 0 | K2: 1 | K3: 3 | K4: 6 |
|---|---|---|---|
 |
 |
 |
 |
| K5: 10 | K6: 15 | K7: 21 | K8: 28 |
 |
 |
 |
 |
| K9: 36 | K10: 45 | K11: 55 | K12: 66 |
 |
 |
 |
 |
Véase también
En inglés: Graph (mathematics) Facts for Kids
