Búsqueda en profundidad para niños
Una Búsqueda en profundidad (conocida como DFS por sus siglas en inglés, Depth First Search) es un método para explorar todos los rincones de un grafo o un árbol. Imagina que estás explorando un laberinto: en lugar de mirar todas las puertas a la vez, eliges un camino y lo sigues hasta el final. Si llegas a un callejón sin salida, retrocedes y pruebas otra puerta cercana. Así es como funciona la búsqueda en profundidad: va lo más lejos posible por un camino antes de volver y explorar otras opciones.
Existe un método similar llamado búsqueda en anchura (BFS o Breadth First Search), que explora todos los caminos cercanos antes de ir más lejos.
Contenido
¿Cómo funciona la Búsqueda en Profundidad?
Este algoritmo funciona como un explorador muy curioso. Cuando llega a un punto (llamado nodo), elige un camino y lo sigue sin desviarse. Si encuentra otro nodo, sigue por ese nuevo camino, y así sucesivamente. Solo cuando llega a un punto sin salida o a un nodo que ya ha visitado, retrocede un paso para probar otro camino que no haya explorado. Este proceso de ir hacia atrás se llama backtracking.
Ejemplo práctico de Búsqueda en Profundidad
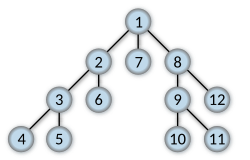
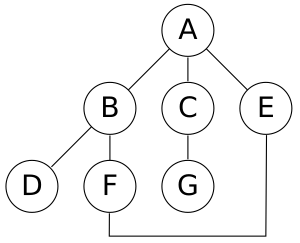
Para entenderlo mejor, veamos un ejemplo con un mapa simple (un grafo):
Imagina que empiezas en el nodo A. Si siempre eliges el camino de la izquierda primero, la búsqueda en profundidad visitaría los nodos en este orden:
- Primero, A.
- De A, va a B.
- De B, va a D.
- De D, va a F.
- De F, no hay más caminos nuevos, así que retrocede a D.
- De D, va a E (el otro camino de D).
- De E, no hay más caminos nuevos, así que retrocede a D, luego a B, y finalmente a A.
- De A, va a C (el otro camino de A).
- De C, va a G.
- De G, no hay más caminos nuevos, así que retrocede a C, y luego a A.
El orden final de visita sería: A, B, D, F, E, C, G.
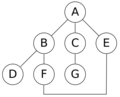
Es importante que el algoritmo recuerde los nodos que ya visitó. Si no lo hiciera, podría quedarse en un círculo infinito, por ejemplo, yendo de A a B, luego a D, F, E, y de E volver a A, repitiendo el ciclo sin fin y sin visitar C o G. Para evitar esto, se usan técnicas como la búsqueda en profundidad iterativa.
¿Para qué se usa la Búsqueda en Profundidad?
La búsqueda en profundidad es muy útil en la informática y las matemáticas. Se usa para:
- Encontrar todos los caminos posibles en un laberinto.
- Verificar si un mapa o red está conectado.
- Organizar información en estructuras de datos como los árboles.
- Resolver rompecabezas o juegos que implican explorar diferentes opciones.
Conceptos importantes de la Búsqueda en Profundidad
¿Es completa la Búsqueda en Profundidad?
Sí, la búsqueda en profundidad es "completa" si el espacio de búsqueda (el mapa o la red) no es infinito y no tiene ciclos que la engañen. Esto significa que, si hay una solución o un camino que buscar, el algoritmo lo encontrará tarde o temprano.
¿Es óptima la Búsqueda en Profundidad?
No siempre. La búsqueda en profundidad no garantiza que encontrará el camino más corto o la mejor solución. Como siempre va lo más profundo posible por un camino, podría encontrar una solución que está muy lejos, incluso si hay una solución más corta en otro camino que aún no ha explorado.
¿Qué tan rápida es la Búsqueda en Profundidad?
La velocidad de la búsqueda en profundidad depende de cuántos nodos y conexiones tenga el grafo. En el peor de los casos, tiene que explorar muchos caminos, lo que puede llevar tiempo. Se mide con algo llamado "complejidad temporal", que nos dice cuánto tiempo podría tardar el algoritmo en completarse.
¿Cuánta memoria necesita la Búsqueda en Profundidad?
La cantidad de memoria que usa la búsqueda en profundidad también depende del tamaño del grafo. Necesita recordar los caminos que ha tomado y los nodos que ha visitado para poder retroceder. Esto se mide con la "complejidad espacial".
Pseudocódigo de la Búsqueda en Profundidad
El pseudocódigo es como una receta escrita en un lenguaje sencillo para que los programadores entiendan cómo funciona el algoritmo antes de escribirlo en un lenguaje de programación real.
DFS(grafo G) PARA CADA vértice u en G HACER estado[u] ← NO_VISITADO padre[u] ← NULO tiempo ← 0 PARA CADA vértice u en G HACER SI estado[u] = NO_VISITADO ENTONCES DFS_Visitar(u,tiempo)
DFS_Visitar(nodo u, int tiempo) estado[u] ← VISITADO tiempo ← tiempo + 1 d[u] ← tiempo PARA CADA v en Vecinos[u] HACER SI estado[v] = NO_VISITADO ENTONCES padre[v] ← u DFS_Visitar(v,tiempo) estado[u] ← TERMINADO tiempo ← tiempo + 1 f[u] ← tiempo
Galería de imágenes
-
Ejemplo de recorrido de grafo.
-
Búsqueda en profundidad. (Orden en el que se visitan los nodos)
Véase también
En inglés: Depth-first search Facts for Kids
