Camino hamiltoniano para niños

En el mundo de las matemáticas, un camino hamiltoniano es como un viaje especial en un mapa. Imagina que tienes un mapa con varios puntos (llamados vértices) y líneas que los conectan (llamadas aristas). Un camino hamiltoniano es una ruta que visita cada punto de tu mapa exactamente una vez.

Si, además de visitar todos los puntos una sola vez, tu viaje termina en el mismo punto donde empezaste, entonces tienes un ciclo hamiltoniano. Es como hacer un recorrido completo y regresar a casa.

Encontrar estos caminos o ciclos en mapas muy grandes puede ser un desafío para las computadoras. Es un problema conocido como "NP-completo", lo que significa que es muy difícil de resolver rápidamente para mapas complejos.

El nombre de "hamiltoniano" viene de un matemático irlandés llamado William Rowan Hamilton. Él propuso un juego en el siglo XIX donde se viajaba entre veinte ciudades, representadas por los puntos de una figura geométrica llamada dodecaedro. El objetivo era visitar cada ciudad una sola vez siguiendo las conexiones.

Sin embargo, la idea de estos caminos especiales es mucho más antigua. En el siglo IX, un poeta de la India llamado Rudrata ya hablaba de un problema similar: el "camino del caballo" en un tablero de ajedrez. Se trata de mover un caballo de ajedrez para que visite cada casilla del tablero exactamente una vez. Esto es, en esencia, encontrar un camino hamiltoniano en un mapa donde las casillas son los puntos y los movimientos del caballo son las conexiones.

¿Qué son los caminos y ciclos hamiltonianos?

Para entender mejor, aquí te explicamos las definiciones clave:

• Un camino hamiltoniano es una secuencia de conexiones que visita todos los puntos de un mapa sin repetir ninguno.
• Un ciclo hamiltoniano es un camino hamiltoniano que empieza y termina en el mismo punto.
• Un mapa (o grafo) que tiene un ciclo hamiltoniano se llama grafo hamiltoniano.

Para los mapas donde las conexiones tienen una dirección (llamados "dígrafos" o grafos dirigidos), las definiciones son parecidas:

• Un camino dirigido hamiltoniano visita todos los puntos sin repetir ninguno, siguiendo la dirección de las conexiones.
• Un ciclo dirigido hamiltoniano es un camino dirigido hamiltoniano que forma un circuito cerrado.
• Un dígrafo es dígrafo hamiltoniano si contiene un ciclo dirigido hamiltoniano.

A diferencia de otros tipos de caminos en mapas (como los caminos eulerianos, que visitan cada conexión una sola vez), no hay una regla sencilla que nos diga si un mapa es hamiltoniano.

Es importante saber que todos los mapas hamiltonianos están "conectados" (puedes ir de cualquier punto a cualquier otro), pero no todos los mapas conectados son hamiltonianos.

Ejemplos de mapas hamiltonianos

Aquí tienes algunos ejemplos de mapas que tienen caminos o ciclos hamiltonianos:

• Los grafos ciclos, que son como anillos o círculos, siempre son hamiltonianos.
• Los grafos completos, donde cada punto está conectado con todos los demás, son hamiltonianos si tienen más de dos puntos.
• Todos los campeonatos (un tipo especial de dígrafo) tienen caminos dirigidos hamiltonianos.
• Las figuras geométricas conocidas como sólidos platónicos (como el tetraedro, el cubo, el octaedro, el dodecaedro y el icosaedro), si los consideramos como mapas, son hamiltonianos.
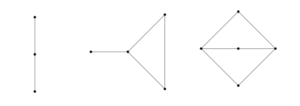
• Algunos mapas pueden ser hamiltonianos y eulerianos a la vez, otros solo uno de ellos, o ninguno.

Grafos: G₁, G₂, G₃ y G₄

• El mapa G₁ es euleriano y hamiltoniano.
• El mapa G₂ es euleriano pero no es hamiltoniano.
• El mapa G₃ no es euleriano pero es hamiltoniano.
• El mapa G₄ no es euleriano y tampoco es hamiltoniano.

Reglas para identificar mapas hamiltonianos

Aunque no hay una regla única, existen algunas condiciones que nos ayudan a saber si un mapa podría ser hamiltoniano.

• Un mapa hamiltoniano siempre debe estar conectado.
• Ningún punto de un mapa hamiltoniano puede tener solo una conexión. Cada punto debe tener al menos dos conexiones: una para "entrar" y otra para "salir" del camino.
• Si quitas un grupo de puntos de un mapa hamiltoniano, el mapa restante no se dividirá en demasiadas partes.

Teorema

Esto significa que un mapa hamiltoniano no puede tener puntos "de corte", que son puntos que, al ser eliminados, dividen el mapa en más partes.

Sin embargo, que un mapa cumpla estas condiciones no significa automáticamente que sea hamiltoniano.

Reglas que garantizan un camino hamiltoniano

Existen reglas más avanzadas que sí nos aseguran que un mapa es hamiltoniano. Para mapas con más de dos puntos, podemos ignorar las conexiones que van de un punto a sí mismo o las conexiones duplicadas entre dos puntos.

Teorema de Bondy-Chvátal

Un teorema importante de J. A. Bondy y V. Chvátal (1976) nos dice que un mapa es hamiltoniano si tiene "suficientes conexiones". Para entenderlo, primero necesitamos saber qué es la "clausura" de un mapa.

Definición Dado un mapa G con n puntos, su clausura es un nuevo mapa que tiene los mismos puntos que G. Se forma añadiendo todas las conexiones posibles entre dos puntos u y v que no estén conectados, siempre y cuando la suma de sus conexiones (el número de líneas que salen de u más el número de líneas que salen de v) sea mayor o igual que el número total de puntos n.

Teorema

Esto es muy útil porque a veces es más fácil saber si la clausura de un mapa es hamiltoniana.

Los teoremas de Ore y Dirac

Como todos los mapas completos (donde cada punto está conectado con todos los demás) son hamiltonianos, si la clausura de un mapa es un mapa completo, entonces el mapa original es hamiltoniano. Esto nos lleva a otros teoremas importantes:

Teorema de Ore

Teorema de Dirac

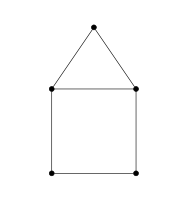
Ejemplo Consideremos el siguiente mapa, conocido como "grafo casa", que claramente es hamiltoniano:

Grafo casa

• No podemos usar el Teorema de Dirac para demostrar que es hamiltoniano, porque algunos puntos tienen solo 2 conexiones, y 2 no es mayor o igual que 5/2 (2.5).
• Tampoco podemos usar el Teorema de Ore, porque hay pares de puntos no conectados donde la suma de sus conexiones es 2 + 2 = 4, y 4 no es mayor o igual que 5.
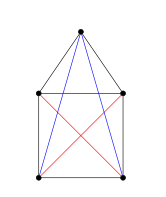
• Sin embargo, si calculamos la clausura del grafo casa, veremos que se convierte en un mapa completo de 5 puntos. Como un mapa completo es hamiltoniano, podemos concluir que el grafo casa es hamiltoniano gracias al Teorema de Bondy-Chvátal.

Clausura del grafo casa

Un resultado relacionado con el Teorema de Ore es el siguiente:

Corolario

Es importante notar que si un mapa cumple esta última condición, no significa que sea necesariamente hamiltoniano (es decir, que tenga un ciclo hamiltoniano), solo que tiene un camino hamiltoniano.

Ejemplos

Dígrafos hamiltonianos

Para los mapas dirigidos (dígrafos), también hay reglas que nos ayudan a saber si son hamiltonianos. Un teorema de H. Meyniel dice:

Teorema

Véase también

En inglés: Hamiltonian path Facts for Kids