Matemática discreta para niños
La matemática discreta es una parte de las matemáticas que estudia cosas que se pueden contar una por una. Imagina que tienes un grupo de objetos que puedes separar y contar individualmente, como los números enteros (1, 2, 3, etc.) o los puntos en un grafo. A diferencia de la matemática continua, que se ocupa de cosas que cambian suavemente, como las curvas o el tiempo, la matemática discreta se enfoca en elementos distintos y separados.
Es muy importante para la ciencia de la computación, porque las computadoras trabajan con información que se puede contar y procesar paso a paso. En la matemática discreta, no se usan ideas como la "proximidad" o los "límites" de una curva. Por ejemplo, un valor puede ser 2 o 3, pero no un número entre ellos que se acerque mucho, como 2.99. Las gráficas en matemática discreta son puntos separados, mientras que en otras áreas de las matemáticas son líneas continuas.
Contenido
¿Cómo surgió la matemática discreta?
La matemática discreta ha resuelto muchos desafíos a lo largo de la historia.
Problemas famosos y sus soluciones
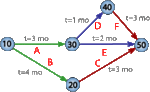
En la teoría de grafos, un área de la matemática discreta, hubo un problema muy famoso llamado el teorema de los cuatro colores. Este teorema dice que cualquier mapa se puede colorear con solo cuatro colores, de modo que dos países vecinos nunca tengan el mismo color. Tardó más de cien años en ser demostrado. Otro problema clásico fue el de los problema de los puentes de Königsberg, resuelto por el matemático Leonhard Euler.
En el campo de la lógica, el matemático David Hilbert propuso varios problemas importantes. Uno de ellos era probar que las reglas básicas de la aritmética eran perfectas y no tenían contradicciones. Sin embargo, en 1931, Kurt Gödel demostró que esto no era posible de probar dentro de la propia aritmética. Otro problema de Hilbert era encontrar una forma general de saber si ciertas ecuaciones tenían soluciones con números enteros. En 1970, Yuri Matiyasevich demostró que esto también era imposible de hacer de forma general.
La matemática discreta y la tecnología
La necesidad de descifrar mensajes secretos durante la Segunda Guerra Mundial impulsó el desarrollo de la criptografía (el estudio de los códigos secretos) y la ciencia computacional teórica. Fue entonces cuando se creó la primera computadora electrónica programable, llamada Colossus, en Inglaterra. Al mismo tiempo, las necesidades militares también llevaron a avances en la investigación de operaciones, que ayuda a tomar decisiones eficientes.
Durante la Guerra Fría, la criptografía siguió siendo muy importante, lo que llevó a la creación de nuevos métodos para proteger la información.
Hoy en día, uno de los problemas más grandes en la informática es el problema de las clases de complejidad "P = NP". El Instituto de Matemáticas Clay ha ofrecido un premio de un millón de dólares a quien lo resuelva.
Áreas de estudio en la matemática discreta
La matemática discreta abarca muchos temas interesantes y útiles.
Informática teórica
Esta área de la matemática discreta es clave para entender cómo funcionan las computadoras. Incluye el estudio de los algoritmos (pasos para resolver problemas), la computabilidad (qué se puede calcular) y la complejidad (cuánto tiempo y recursos se necesitan para calcular algo). También se relaciona con los lenguajes formales y la teoría de autómatas, que son como modelos de máquinas que procesan información.
Teoría de la información
Esta teoría se encarga de medir la cantidad de información. También incluye la teoría de codificación, que ayuda a crear formas eficientes y seguras de enviar y guardar datos.
Lógica
La lógica es el estudio de cómo razonamos correctamente. Nos ayuda a entender qué afirmaciones son válidas y cómo se construyen las pruebas. Por ejemplo, las tablas de verdad se usan para verificar si una afirmación lógica es verdadera o falsa. La lógica es fundamental para la demostración automática de teoremas y para verificar que los programas de computadora funcionen bien.
Teoría de conjuntos
La teoría de conjuntos estudia las colecciones de objetos, como el conjunto de los colores {azul, blanco, rojo} o el conjunto de todos los números primos. En la matemática discreta, nos interesan principalmente los conjuntos que se pueden contar, ya sean finitos o infinitos.
Combinatoria
La combinatoria es la rama de la matemática que estudia cómo se pueden combinar u ordenar objetos en colecciones finitas. Por ejemplo, si tienes varias camisetas y pantalones, la combinatoria te ayuda a saber cuántos conjuntos diferentes puedes formar.
- Combinatoria enumerativa: Se dedica a "contar" cuántos objetos hay en estas colecciones.
- Teoría de grafos: Es el estudio de los grafos, que son conjuntos de puntos (vértices) conectados por líneas (aristas). Se usa para modelar redes, como las redes sociales o las carreteras.
Probabilidad discreta
La teoría de distribuciones de probabilidad discretas se ocupa de eventos que tienen un número contable de resultados posibles. Por ejemplo, el número de veces que sale "cara" al lanzar una moneda varias veces.
Teoría de números

La teoría de números se enfoca en las propiedades de los enteros. Es muy importante en la criptografía, especialmente con los número primos, para crear códigos seguros.
Álgebra
El álgebra también tiene ramas discretas. Por ejemplo, el álgebra booleana es fundamental para el diseño de circuitos digitales y la programación de computadoras. También se usan grupos, anillos y campos en la teoría de códigos.
Cálculo de diferencias finitas
Una sucesión es una función definida para números enteros. Puede ser finita o infinita. Las ecuaciones de diferencia son similares a las ecuaciones diferenciales, pero en lugar de cambios continuos, se enfocan en las diferencias entre términos adyacentes.
Geometría discreta
La geometría discreta estudia las propiedades de colecciones de objetos geométricos separados. Un ejemplo es cómo cubrir un plano con formas sin dejar huecos (teselados). La geometría computacional usa algoritmos para resolver problemas geométricos.
Topología
La topología estudia las propiedades de los objetos que no cambian cuando se estiran o doblan sin romperlos. Aunque la topología general trata con la continuidad, muchas de sus ramas, como la topología combinatoria y la topología algebraica, tienen aspectos discretos.
Investigación Operativa
La investigación operativa usa modelos matemáticos y algoritmos para ayudar a tomar decisiones prácticas en negocios y otras áreas. Por ejemplo, cómo asignar recursos para obtener el mayor beneficio o cómo organizar actividades para reducir riesgos. Incluye técnicas como la programación lineal y la teoría de colas.
Teoría de juegos y decisión
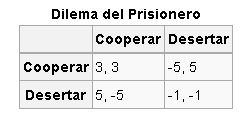
La teoría de la decisión ayuda a identificar los factores importantes para tomar una decisión y elegir la mejor opción. La teoría de juegos estudia situaciones donde el éxito de una persona depende de las decisiones de otros, lo que hace que elegir la mejor acción sea más complejo.
Discretización
La discretización es el proceso de transformar modelos y ecuaciones continuos en sus versiones discretas. Esto se hace a menudo para facilitar los cálculos, especialmente en el análisis numérico.
Otros temas relacionados
- álgebra lineal – el estudio de funciones lineales.
- algoritmia – el estudio de métodos de cálculos.
- probabilidad y cadenas de Markov
- teoría de la computabilidad y de la complejidad - que tratan sobre lo que se puede calcular y sus límites.
Véase también
 En inglés: Discrete mathematics Facts for Kids
En inglés: Discrete mathematics Facts for Kids