Teoría de conjuntos para niños

Un diagrama de Venn que ilustra la intersección de dos conjuntos.

La teoría de conjuntos es una parte de la lógica matemática que estudia los conjuntos. Un conjunto es una colección de objetos, que pueden ser números, letras, o incluso otros conjuntos. Esta teoría es una herramienta fundamental en matemáticas. Nos ayuda a entender y construir otras ideas matemáticas. Por ejemplo, los números, las funciones y las figuras geométricas se pueden explicar usando conjuntos.

Además de ser una herramienta, la teoría de conjuntos también se estudia por sí misma. Especialmente, se investigan las propiedades de los conjuntos infinitos. A veces, en esta área, surgen preguntas muy difíciles. Algunas propiedades pueden ser imposibles de demostrar o incluso parecer contradictorias. Por eso, la lógica matemática es muy importante aquí.

El matemático Georg Cantor fue quien empezó a desarrollar la teoría de conjuntos. Esto ocurrió a finales del siglo XIX. Otros matemáticos como Bernhard Bolzano y Richard Dedekind también tuvieron ideas importantes. Más tarde, se descubrieron algunas paradojas (situaciones que parecen contradecirse) en la teoría de Cantor. Esto llevó a otros matemáticos como Bertrand Russell, Ernst Zermelo y Abraham Fraenkel a trabajar en cómo hacer la teoría más sólida.

Hoy en día, la teoría de conjuntos se usa como base para casi todas las matemáticas. Una versión muy usada es la teoría de conjuntos de Zermelo-Fraenkel, que incluye el axioma de elección. Además de su papel fundamental, la teoría de conjuntos nos permite estudiar el concepto de infinito de una manera matemática. También tiene aplicaciones en informática, filosofía y en el estudio del significado de las palabras (semántica formal).

Historia de la Teoría de Conjuntos

Georg Cantor, el fundador de la teoría de conjuntos.

Aunque muchas ideas matemáticas se desarrollan con el tiempo por varios investigadores, la teoría de conjuntos moderna fue iniciada por un solo artículo. Fue escrito por Georg Cantor en 1874. Se titulaba Sobre una propiedad de la colección de todos los números algebraicos reales.

Desde hace mucho tiempo, los matemáticos han pensado en el concepto de infinito. Ya en el siglo V a. C., el griego Zenón de Elea y matemáticos de la India exploraron esta idea. En el siglo XIX, Bernard Bolzano también hizo contribuciones. Pero la forma en que entendemos el infinito hoy comenzó con el trabajo de Cantor entre 1870 y 1874. Una reunión con Richard Dedekind en 1872 influyó mucho en Cantor.

Al principio, el trabajo de Cantor generó opiniones divididas. Algunos matemáticos como Karl Weierstrass y Dedekind lo apoyaron. Otros, como Leopold Kronecker, no estaban de acuerdo. Sin embargo, las ideas de Cantor se hicieron muy populares. Esto se debe a conceptos útiles como la correspondencia uno a uno entre conjuntos. También demostró que hay más números reales que números enteros. Y que existen "infinitos de infinitos", lo que Cantor llamó su "paraíso".

Alrededor de 1900, se descubrió que algunas interpretaciones de la teoría de Cantor llevaban a contradicciones. Estas se llamaron antinomias o paradojas. Bertrand Russell y Ernst Zermelo descubrieron de forma independiente la Paradoja de Russell. Esta paradoja pregunta sobre "el conjunto de todos los conjuntos que no son miembros de sí mismos". Lleva a una contradicción porque si es miembro de sí mismo, no debería serlo, y si no es miembro de sí mismo, entonces sí debería serlo.

A pesar de estas paradojas, la teoría de conjuntos no fue abandonada. Los trabajos de Zermelo en 1908, y de Abraham Fraenkel y Thoralf Skolem en 1922, llevaron a los axiomas ZFC. Estos son los axiomas más usados para la teoría de conjuntos. El trabajo de matemáticos como Henri Lebesgue mostró lo útil que era la teoría de conjuntos. Desde entonces, se ha convertido en una parte esencial de las matemáticas modernas.

Conceptos Básicos de Conjuntos

La teoría de conjuntos más sencilla es una herramienta fundamental en el lenguaje matemático. De hecho, todas las matemáticas modernas se pueden explicar usando conjuntos. Por eso, estudiar la teoría de conjuntos es clave para entender los fundamentos de las matemáticas.

La idea principal es que los conjuntos son ideas abstractas que contienen elementos. Estos elementos pueden ser otros objetos matemáticos, como números o polígonos. Podemos imaginar una colección específica de estos objetos, y esa colección es un conjunto. Cada uno de estos objetos pertenece al conjunto. Esta idea de pertenencia es la relación más básica en la teoría de conjuntos. Los conjuntos mismos también pueden ser elementos de otros conjuntos. Si un elemento $a$ pertenece a un conjunto $A$ , lo escribimos como $a \in A$ .

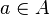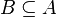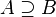Otra relación importante entre conjuntos es la inclusión. Si todos los elementos de un conjunto $B$ también están en un conjunto $A$ , entonces $B$ es un subconjunto de $A$ . Esto se escribe como $B \subseteq A$ (se lee " $B$ está incluido en $A$ "). También podemos decir que $A$ contiene a $B$ , y se escribe $A \supseteq B$ .

Ejemplos de Conjuntos

Los conjuntos numéricos más comunes en matemáticas son:
- Los números naturales (N): 1, 2, 3, ...
- Los números enteros (Z): ..., -2, -1, 0, 1, 2, ...
- Los números racionales (Q): fracciones como 1/2, 3/4, etc.
- Los números reales (R): todos los números que puedes imaginar en una línea, incluyendo los decimales infinitos.
- Los números complejos (C): números que incluyen la raíz cuadrada de -1.

Cada uno de estos conjuntos es un subconjunto del siguiente:

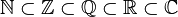
$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$

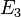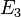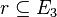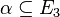El espacio tridimensional $E_3$ es un conjunto de puntos. Las rectas $r$ y los planos $\alpha$ son conjuntos de puntos. Por lo tanto, son subconjuntos de $E_3$ , es decir, $r \subseteq E_3$ y $\alpha \subseteq E_3$ .

Operaciones con Conjuntos

Así como hay operaciones aritméticas (suma, resta), también hay operaciones básicas para manipular conjuntos. Esto se conoce como el álgebra de conjuntos.

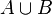Unión: La unión de dos conjuntos $A$ y $B$ es el conjunto $A \cup B$ . Contiene todos los elementos que están en $A$ , en $B$ , o en ambos.

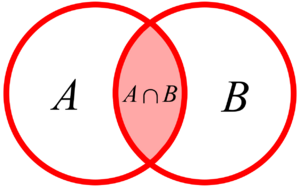
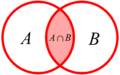
Intersección: La intersección de dos conjuntos $A$ y $B$ es el conjunto $A \cap B$ . Contiene solo los elementos que son comunes a $A$ y a $B$ .

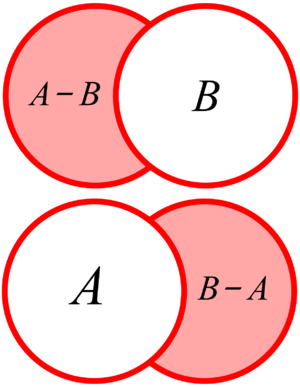
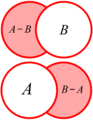
Diferencia: La diferencia entre dos conjuntos $A$ y $B$ es el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A - B . Contiene todos los elementos de $A$ que NO están en $B$ . Es importante saber que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A - B no es lo mismo que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): B - A .

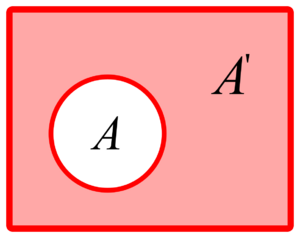
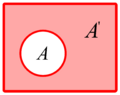
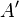Complemento: El complemento de un conjunto $A$ es el conjunto $A'$ . Contiene todos los elementos que NO pertenecen a $A$ , pero sí a un conjunto de referencia más grande.

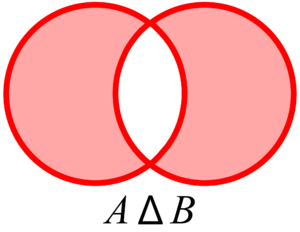
Diferencia Simétrica: La diferencia simétrica de dos conjuntos $A$ y $B$ es el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A \Delta B . Contiene todos los elementos que están en $A$ o en $B$ , pero NO en ambos a la vez.

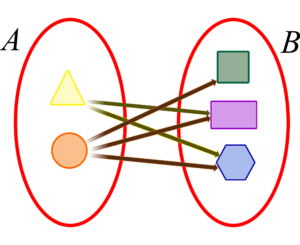
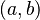Producto Cartesiano: El producto cartesiano de dos conjuntos $A$ y $B$ es el conjunto Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A \times B . Contiene todos los pares ordenados $(a, b)$ , donde el primer elemento $a$ es de $A$ y el segundo $b$ es de $B$ .

Los diagramas de Venn son una forma visual de representar conjuntos y sus operaciones.

Ejemplo Práctico

Imagina un examen donde:

20 estudiantes respondieron bien la primera pregunta.
23 estudiantes respondieron bien la segunda pregunta.
9 estudiantes respondieron bien AMBAS preguntas.
12 estudiantes respondieron MAL AMBAS preguntas.

¿Cuántos estudiantes en total hicieron el examen?

Resolución:

Llamemos $A$ al conjunto de estudiantes que respondieron bien la primera pregunta.
Llamemos $B$ al conjunto de estudiantes que respondieron bien la segunda pregunta.
La intersección $A \cap B$ son los que respondieron bien ambas.
Los que respondieron mal ambas son Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): A' \cap B' .

Tenemos:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A|=20
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |B|=23
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A \cap B|=9
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): |A' \cap B'|= 12

Para encontrar el total, usamos la fórmula: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Total = |A| + |B| - |A \cap B| + |A' \cap B'|

Sustituyendo los números: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): Total = 20 + 23 - 9 + 12 = 46 estudiantes.

Así, 46 estudiantes hicieron el examen.

Teoría Axiomática de Conjuntos

La teoría de conjuntos que se basa solo en la intuición puede llevar a problemas. Por ejemplo, la famosa paradoja de Russell muestra una contradicción. Por eso, se desarrollaron las teorías axiomáticas de conjuntos. Estas teorías usan un conjunto de reglas o axiomas muy precisos. El objetivo es construir todas las propiedades de los conjuntos de manera lógica y sin contradicciones.

Algunas teorías axiomáticas de conjuntos conocidas son:

La teoría de conjuntos de Zermelo-Fraenkel (ZFC).
La teoría de conjuntos de Neumann-Bernays-Gödel.
La teoría de conjuntos de Morse-Kelley.

Áreas de Estudio en Teoría de Conjuntos

La teoría de conjuntos es un campo de investigación activo en matemáticas, con varias ramas:

Teoría de Conjuntos Combinatoria

Esta área aplica ideas de la combinatoria (que estudia cómo contar y organizar cosas) a los conjuntos infinitos. Incluye el estudio de la aritmética cardinal (que compara el "tamaño" de los infinitos) y extensiones de teoremas como el teorema de Ramsey.

Teoría Descriptiva de Conjuntos

La teoría descriptiva de conjuntos estudia los subconjuntos de la recta real y otros espacios. Se enfoca en cómo se pueden describir y clasificar estos conjuntos. A menudo, para demostrar propiedades de conjuntos más complejos, se necesitan axiomas adicionales.

Teoría de Conjuntos Difusos

En la teoría de conjuntos tradicional, un objeto o es miembro de un conjunto o no lo es. En la teoría de conjuntos difusos, esta regla se relaja. Un objeto puede tener un grado de pertenencia a un conjunto, que es un número entre 0 y 1. Por ejemplo, una persona puede tener un grado de pertenencia de 0.75 al conjunto de "personas altas", en lugar de un simple sí o no.

Cardinales Grandes

Un cardinal grande es un número cardinal con una propiedad especial. Se estudian muchas de estas propiedades, como los cardinales inaccesibles. Estas propiedades suelen implicar que el número cardinal es extremadamente grande. La existencia de un cardinal con estas propiedades no se puede demostrar con los axiomas normales de la teoría de conjuntos.

Forzamiento

Paul Cohen inventó el método de forzamiento. Lo usó para crear modelos de la teoría de conjuntos donde ciertas afirmaciones (como la hipótesis del continuo) no son verdaderas. El forzamiento añade conjuntos a un modelo existente para crear uno nuevo con propiedades específicas.

Objeciones a la Teoría de Conjuntos

Desde sus inicios, algunos matemáticos han tenido objeciones a la teoría de conjuntos como base de las matemáticas.

Una objeción común, expresada por Leopold Kronecker, viene de la idea de que las matemáticas están relacionadas con la computación. Si se acepta esto, entonces el manejo de conjuntos infinitos introduce métodos que no se pueden calcular.

Otra objeción, de Henri Poincaré, es que la forma en que se definen los conjuntos puede llevar a un tipo de circularidad.

Ludwig Wittgenstein criticó filosóficamente la teoría de conjuntos. Pensaba que hablar de "todos los números" no tenía sentido. Él veía las matemáticas como deducción humana y finita.

Hoy en día, se exploran otras bases para las matemáticas. Por ejemplo, la teoría de los topos es una alternativa a la teoría axiomática de conjuntos tradicional. También, los fundamentos univalentes y la Teoría de tipos homotópica son áreas de investigación activas que ofrecen nuevas formas de entender los conjuntos y los principios matemáticos.

Galería de imágenes

Un diagrama de Venn que ilustra la intersección de dos conjuntos.
Un diagrama de Venn que ilustra la unión de dos conjuntos.
Un diagrama de Venn que ilustra la diferencia entre dos conjuntos.
Un diagrama de Venn que ilustra el complemento de un conjunto.
Un diagrama de Venn que ilustra la diferencia simétrica entre dos conjuntos.
Un diagrama de Venn que ilustra el producto cartesiano de dos conjuntos.
Un segmento inicial de la jerarquía o universo de von Neumann.

Véase también

En inglés: Set theory Facts for Kids

Álgebra de conjuntos
Teoría de axiomática de conjuntos
Conjunto
Dinámica de sistemas
Equipotencia de conjuntos
Teoría de grupos
Diagramas de Venn

Obtenido de «https://ninos.kiddle.co/index.php?title=Teoría_de_conjuntos&oldid=5004469»

Todo el contenido de los artículos de la Enciclopedia Kiddle (incluidas las imágenes) se puede utilizar libremente para fines personales y educativos bajo la licencia Atribución-CompartirIgual a menos que se indique lo contrario. Citar este artículo:

Teoría de conjuntos para Niños. Enciclopedia Kiddle.