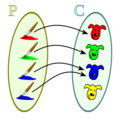
Función biyectiva para niños

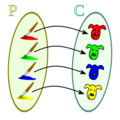
En matemáticas, una función es biyectiva cuando es como un emparejamiento perfecto entre dos grupos de elementos. Imagina que tienes dos grupos, uno de "salida" y otro de "llegada". Una función biyectiva asegura que:

• Cada elemento del grupo de salida tiene un compañero único en el grupo de llegada.
• Cada elemento del grupo de llegada tiene un compañero único en el grupo de salida.

Esto significa que no sobra ningún elemento en ninguno de los dos grupos y que no hay elementos que tengan más de un compañero. Es como si cada persona tuviera exactamente un asiento y cada asiento estuviera ocupado por exactamente una persona.

¿Qué es una función biyectiva?

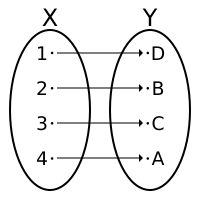
Una función que va de un conjunto (el grupo de salida) a un conjunto 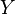(el grupo de llegada) se llama biyectiva si cumple dos condiciones importantes:

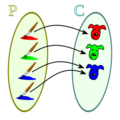
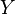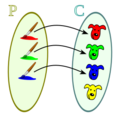
• Es inyectiva: Esto significa que cada elemento del grupo de salida se conecta con un elemento diferente en el grupo de llegada. No hay dos elementos de que apunten al mismo elemento en . Piensa en ello como si cada persona tuviera su propio asiento, y nadie compartiera asiento.
• Es sobreyectiva: Esto significa que todos los elementos del grupo de llegada tienen al menos un compañero en el grupo de salida. No hay elementos en 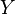que se queden sin ser "alcanzados" por un elemento de . Es como si todos los asientos estuvieran ocupados.

Cuando una función es inyectiva y sobreyectiva al mismo tiempo, ¡es biyectiva!

La función inversa y las funciones biyectivas

Si una función es biyectiva, siempre podemos encontrar su "función inversa". Piensa en la función original como un camino de ida, y la función inversa como el camino de vuelta. Si el camino de ida es biyectivo (un emparejamiento perfecto), el camino de vuelta también lo será.

Por ejemplo, la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f(x) = 2x + 3 es biyectiva. Esto significa que para cada número que le des, obtendrás un resultado único, y para cada resultado , hay un único que lo produce.

Su función inversa sería Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f^{-1}(x) = \frac{x - 3}{2} , y esta también es biyectiva.

Ejemplos de funciones biyectivas

Alumnos y asientos en un aula

Imagina una clase con varios asientos. Un grupo de estudiantes entra y el profesor les pide que se sienten. Después de mirar, el profesor dice que hay una "biyectividad" entre los estudiantes y los asientos. ¿Qué observó el profesor para decir esto?

1. Todos los estudiantes estaban sentados (nadie estaba de pie). (Esto es la parte sobreyectiva: todos los "asientos" -los estudiantes- tienen un "compañero" -un asiento-).
2. Ningún estudiante estaba sentado en más de un asiento. (Esto es parte de la inyectividad: cada "elemento de salida" -estudiante- tiene un único "elemento de llegada" -asiento-).
3. Cada asiento estaba ocupado (no había asientos vacíos). (Esto es la parte sobreyectiva: todos los "elementos de llegada" -asientos- tienen un "compañero" -estudiante-).
4. Ningún asiento estaba ocupado por más de un estudiante. (Esto es parte de la inyectividad: cada "elemento de llegada" -asiento- tiene un único "elemento de salida" -estudiante-).

Gracias a estas observaciones, el profesor pudo saber que había exactamente la misma cantidad de estudiantes que de asientos, ¡sin necesidad de contarlos!

¿Cómo se relaciona la biyectividad con el tamaño de los conjuntos?

Ejemplo de función biyectiva entre dos conjuntos finitos, donde se puede ver que tienen el mismo número de elementos.

Cuando dos conjuntos (grupos de elementos) tienen una función biyectiva entre ellos, significa que tienen el mismo "tamaño" o la misma cantidad de elementos. Esto es muy útil en matemáticas, incluso para conjuntos que tienen infinitos elementos.

Si podemos encontrar una función biyectiva entre dos conjuntos e 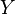, entonces decimos que tienen la misma cardinalidad (el mismo número de elementos). Esto se escribe como:

Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mbox{card}(X) = \mbox{card}(Y)\,

Galería de imágenes

• 

  Función inyectiva y sobreyectiva (biyectiva)

• 

  Función sobreyectiva, pero no inyectiva

• 

  Función inyectiva, pero no sobreyectiva

• 

  Función que no es inyectiva ni sobreyectiva

Véase también

En inglés: Bijective function Facts for Kids

• Correspondencia matemática
• Biyección, inyección y sobreyección