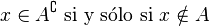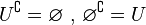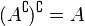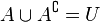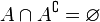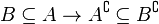Complemento de un conjunto para niños
El complemento de un conjunto es como el "otro lado" de un grupo de cosas. Imagina que tienes un grupo de elementos, y quieres saber cuáles elementos NO están en ese grupo. Esos elementos que quedan fuera forman el conjunto complementario.
Para entender esto bien, siempre necesitamos saber de qué "universo" o grupo más grande estamos hablando. A este grupo grande se le llama conjunto universal. Por ejemplo, si nuestro universo son todos los números naturales (1, 2, 3, 4, ...), y tenemos el conjunto de los números primos (2, 3, 5, 7, ...), su complemento serían todos los números naturales que no son primos. Es decir, el 1 y los números compuestos (4, 6, 8, 9, ...).
El complemento de un conjunto A se puede escribir de varias formas, como A con una pequeña "c" arriba (Ac) o con una barra encima (Ā).
Contenido
¿Qué es el Complemento de un Conjunto?
Entendiendo el Conjunto Universal
Para encontrar el complemento de un conjunto, primero debemos saber cuál es el conjunto universal (U). Este es el grupo más grande de todos los elementos que estamos considerando. Si no definimos este universo, sería difícil saber qué elementos "no están" en nuestro conjunto.
Por ejemplo, si hablamos de frutas, nuestro conjunto universal podría ser "todas las frutas". Si nuestro conjunto es "manzanas", su complemento serían "todas las frutas que no son manzanas" (peras, plátanos, naranjas, etc.).
Cómo se define el Complemento
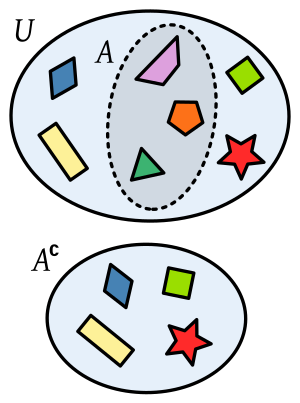
El complemento de un conjunto A (que se escribe como Ac) es el conjunto de todos los elementos que pertenecen al conjunto universal U, pero que NO están en A.
Podemos escribirlo así:
|
Esto significa que un elemento x está en el complemento de A si y solo si x no está en A.
Ejemplos Sencillos
- Si el conjunto universal son todas las personas, y el conjunto A son los hombres, entonces el complemento de A son las mujeres.
- Si el conjunto universal son los números naturales (1, 2, 3, ...), y el conjunto B es {1, 5, 6, 7, 8, 10}, entonces el complemento de B es {2, 3, 4, 9, 11, 12, ...}.
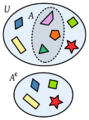
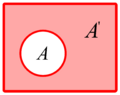
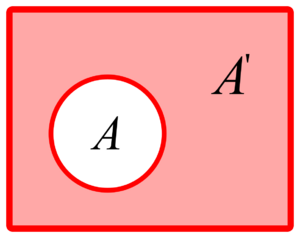
- En la imagen de al lado, el conjunto universal U es todo el rectángulo. Si el conjunto A es el círculo, su complemento Ac es la zona sombreada de azul, es decir, todo lo que está en el rectángulo pero fuera del círculo.
Propiedades Importantes del Complemento
El complemento tiene algunas propiedades interesantes que nos ayudan a entender cómo funciona:
- El complemento del universo y del conjunto vacío:
* El complemento del conjunto universal (U) es el conjunto vacío (Ø), porque no hay nada fuera de "todo". * El complemento del conjunto vacío (Ø) es el conjunto universal (U), porque "todo" está fuera de "nada".
|
|
- El complemento del complemento: Si tomas el complemento de un conjunto, y luego tomas el complemento de ese resultado, vuelves al conjunto original. Es como decir "lo que no es no-A, es A".
|
|
- Unión de un conjunto y su complemento: Si juntas un conjunto con su complemento, obtienes el conjunto universal completo.
|
|
- Intersección de un conjunto y su complemento: Un conjunto y su complemento no tienen elementos en común. Su intersección es el conjunto vacío.
|
|
- Relación con los subconjuntos: Si un conjunto B está dentro de un conjunto A (es un subconjunto), entonces el complemento de A estará dentro del complemento de B.
|
|
Leyes de De Morgan
Estas leyes nos muestran cómo el complemento se relaciona con la unión y la intersección de conjuntos:
- El complemento de la unión de dos conjuntos es igual a la intersección de sus complementos.
|
|
- El complemento de la intersección de dos conjuntos es igual a la unión de sus complementos.
|
|
Galería de imágenes
-
Complementario de un conjunto A.
Véase también
- Álgebra de conjuntos
- Conjunto
- Teoría de conjuntos
- Diferencia de conjuntos
- Unión de conjuntos
- Diferencia simétrica
Referencias
-
Esta obra contiene una traducción parcial derivada de «Complementary relation» de Wikipedia en inglés, publicada por sus editores bajo la Licencia de documentación libre de GNU y la Licencia Creative Commons Atribución-CompartirIgual 3.0 Unported.
- Lipschutz, Seymour (1991). Teoría de conjuntos y temas afines. McGraw-Hill. ISBN 968-422-926-7.