Producto cartesiano para niños
El producto cartesiano es una operación matemática que se usa para combinar elementos de dos conjuntos. Imagina que tienes dos grupos de cosas, por ejemplo, un grupo de frutas y un grupo de colores. El producto cartesiano te ayuda a crear todas las combinaciones posibles, donde cada combinación tiene una fruta y un color. El resultado es un nuevo conjunto formado por "pares ordenados". Un par ordenado es como una pareja de elementos donde el orden importa, por ejemplo, (manzana, rojo) es diferente de (rojo, manzana).
Este concepto lleva el nombre de René Descartes, un famoso matemático y filósofo francés. Sus ideas sobre la geometría analítica, que une el álgebra con la geometría, fueron clave para entender cómo se forman estos pares ordenados y cómo se pueden representar en un plano.
Contenido
¿Cómo funciona el producto cartesiano?
Para entenderlo mejor, veamos cómo se forma el producto cartesiano de dos conjuntos.
Un ejemplo sencillo
Imagina que tienes dos conjuntos:
- El conjunto A tiene los números: {1, 2, 3, 4}
- El conjunto B tiene las letras: {a, b}
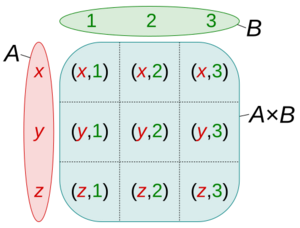
Si queremos encontrar el producto cartesiano de A por B (que se escribe A × B), lo que hacemos es formar todos los pares ordenados posibles, donde el primer elemento viene de A y el segundo de B.
Así, A × B sería:
- (1, a)
- (1, b)
- (2, a)
- (2, b)
- (3, a)
- (3, b)
- (4, a)
- (4, b)
Entonces, el conjunto A × B es: {(1, a), (1, b), (2, a), (2, b), (3, a), (3, b), (4, a), (4, b)}.
Ahora, ¿qué pasa si hacemos el producto cartesiano de B por A (B × A)? En este caso, el primer elemento viene de B y el segundo de A.
Así, B × A sería:
- (a, 1)
- (a, 2)
- (a, 3)
- (a, 4)
- (b, 1)
- (b, 2)
- (b, 3)
- (b, 4)
El conjunto B × A es: {(a, 1), (a, 2), (a, 3), (a, 4), (b, 1), (b, 2), (b, 3), (b, 4)}.
Como puedes ver, (1, a) no es lo mismo que (a, 1). Esto demuestra que el orden de los elementos en un par ordenado es muy importante.
Representando puntos en un plano
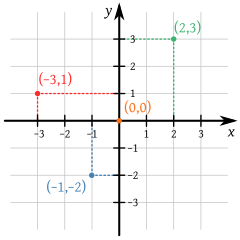
Un uso muy común del producto cartesiano es para representar puntos en un plano cartesiano. Por ejemplo, si tomamos el conjunto de todos los números enteros (..., -2, -1, 0, 1, 2, ...), y hacemos el producto cartesiano de este conjunto consigo mismo, obtenemos pares como (0,0), (0,1), (1,0), (-1,2), etc.
Cada uno de estos pares representa un punto en un plano. El primer número te dice dónde moverte en el eje horizontal (eje X) y el segundo número te dice dónde moverte en el eje vertical (eje Y).
Un ejemplo con objetos
Imagina que tienes un conjunto de tubos de pintura (T) y un conjunto de pinceles (P).
- T = {pintura roja, pintura azul, pintura verde, pintura amarilla}
- P = {pincel fino, pincel mediano, pincel grueso}
El producto cartesiano T × P te daría todas las combinaciones posibles de un tubo de pintura con un pincel:
- (pintura roja, pincel fino)
- (pintura roja, pincel mediano)
- (pintura roja, pincel grueso)
- (pintura azul, pincel fino)
- ... y así sucesivamente con todas las pinturas.
Este tipo de combinaciones es muy útil en muchas áreas, desde la informática hasta la organización de datos.
Propiedades importantes
El producto cartesiano tiene algunas propiedades que es bueno conocer:
El conjunto vacío
Si uno de los conjuntos que usas para el producto cartesiano está vacío (es decir, no tiene ningún elemento), el resultado del producto cartesiano también será un conjunto vacío. Esto tiene sentido, porque no puedes formar pares si no hay elementos en uno de los grupos.
El orden importa
Como vimos en el ejemplo de los números y las letras, el producto cartesiano no es "conmutativo". Esto significa que A × B no es lo mismo que B × A, a menos que los conjuntos sean iguales o uno de ellos esté vacío. El orden en que combinas los conjuntos sí cambia el resultado.
Contar los elementos
Si tienes dos conjuntos finitos (con un número limitado de elementos), el número total de elementos en su producto cartesiano es igual a la multiplicación del número de elementos de cada conjunto. Por ejemplo, si el conjunto A tiene 4 elementos y el conjunto B tiene 2 elementos, A × B tendrá 4 × 2 = 8 elementos.
Galería de imágenes
Véase también
 En inglés: Cartesian product Facts for Kids
En inglés: Cartesian product Facts for Kids