Par ordenado para niños
En matemáticas, un par ordenado es una pareja de objetos donde el orden en que aparecen es muy importante. Imagina que tienes dos cosas, por ejemplo, un número y una letra. Si el orden importa, no es lo mismo decir "el número 5 y la letra A" que "la letra A y el número 5".
Un par ordenado se escribe usando paréntesis y una coma entre los elementos, así: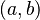 
. Aquí, 
es el primer elemento y 
es el segundo.
Es importante saber que un par ordenado 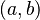no es lo mismo que un conjunto que contiene a los elementos y , que se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{a,b\} . En un conjunto, el orden no importa; por ejemplo,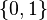 
y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \{1,0\} son el mismo conjunto. Pero en un par ordenado, el orden sí importa: 
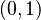y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (1,0) son diferentes.
Los pares ordenados también se pueden llamar tuplas o vectores dimensionales. Cuando tenemos más de dos objetos en un orden específico, hablamos de n-tuplas (por ejemplo, una "terna" si son tres objetos).
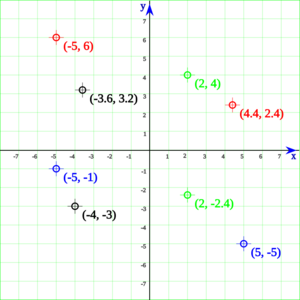
Los pares ordenados son muy útiles en matemáticas. Se usan para definir cosas como las coordenadas cartesianas (que nos ayudan a ubicar puntos en un mapa o en un gráfico), las relaciones y las funciones.
Contenido
¿Qué es un Par Ordenado?
Un par ordenado es una forma de agrupar dos elementos donde el lugar que ocupa cada uno es clave. Piensa en las coordenadas de un punto en un mapa: el primer número te dice cuánto moverte a la derecha o izquierda, y el segundo, cuánto moverte hacia arriba o abajo. Si cambias el orden, ¡llegas a un lugar diferente!
¿Por qué el Orden Importa en un Par Ordenado?
La característica principal de un par ordenado es que su definición incluye el orden de sus elementos. Esto significa que:
- El par ordenado 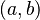es igual al par ordenado Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (c,d) solo si el primer elemento de uno es igual al primer elemento del otro (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a=c ), Y el segundo elemento de uno es igual al segundo elemento del otro (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b=d ).
Por ejemplo, el par ordenado Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (2,5) es diferente de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (5,2) . En el primer caso, el 2 es el primer elemento y el 5 es el segundo. En el segundo caso, es al revés. Los elementos de un par ordenado también se llaman componentes.
¿Para Qué Usamos los Pares Ordenados?
Los pares ordenados son fundamentales en muchas áreas de las matemáticas:
- Coordenadas: Son la base de los sistemas de coordenadas, como el plano cartesiano, donde cada punto se representa con un par ordenado
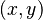. - Relaciones: Ayudan a definir cómo se relacionan los elementos de dos conjuntos.
- Funciones: Una función se puede ver como un conjunto de pares ordenados donde cada primer elemento tiene un único segundo elemento asociado.
El Producto Cartesiano: Combinando Elementos
Cuando tenemos dos grupos de cosas (llamados conjuntos), podemos formar un nuevo grupo con todos los pares ordenados posibles. A esto se le llama producto cartesiano.
Por ejemplo, si tienes un conjunto de colores (Rojo, Azul) y un conjunto de tamaños (Pequeño, Grande), el producto cartesiano sería:
- (Rojo, Pequeño)
- (Rojo, Grande)
- (Azul, Pequeño)
- (Azul, Grande)
Este producto se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): X \times Y , donde 
es el primer conjunto e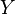 
es el segundo.
Generalizaciones: Más Allá de Dos Elementos
A veces necesitamos agrupar más de dos objetos en un orden específico. Para esto, extendemos la idea del par ordenado. Por ejemplo:
- Un trío ordenado o terna ordenada es un grupo de tres objetos donde el orden importa. Se escribe como Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a_1, a_2, a_3) .
- La regla de igualdad es similar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (a_1, a_2, a_3) es igual a Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (b_1, b_2, b_3) solo si Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_1 = b_1 , Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_2 = b_2 y Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): a_3 = b_3 .
En general, podemos tener una n-tupla, que es un grupo ordenado de n elementos.
Véase también
En inglés: Ordered pair Facts for Kids
- Par desordenado
