Distancia para niños
En matemáticas, la distancia es la medida de lo lejos que están dos puntos o lugares. Imagina que quieres ir de un punto a otro; la distancia es la longitud del camino más corto entre ellos. En un espacio plano, como una hoja de papel, este camino es una línea recta.
En física, la distancia es una cantidad que solo tiene un valor (no tiene dirección), y se mide en unidades de longitud como metros o kilómetros.
Contenido
¿Cómo se calcula la distancia?
Distancia en una línea recta
Piensa en una línea numérica, como una regla. Cada punto en la línea tiene un número. Si tienes dos puntos, A y B, con números `x1` y `x2`, la distancia entre ellos se calcula restando sus números y tomando el valor absoluto (siempre positivo).
Por ejemplo, si A está en el 3 y B en el 7, la distancia es `|7 - 3| = 4`. Si A está en el -2 y B en el 5, la distancia es `|5 - (-2)| = |5 + 2| = 7`.
Distancia entre dos puntos en un plano
Cuando tienes dos puntos en un plano, como en un mapa con coordenadas (x, y), puedes usar el famoso Teorema de Pitágoras para calcular la distancia.
Imagina que tienes el punto A con coordenadas `(x1, y1)` y el punto B con `(x2, y2)`. Puedes formar un triángulo rectángulo usando estos dos puntos y un tercer punto auxiliar. La distancia entre A y B será la hipotenusa de ese triángulo.
La fórmula para calcular la distancia `d(AB)` es: 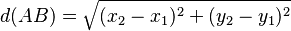
Esta fórmula te dice que debes restar las coordenadas `x`, elevar el resultado al cuadrado; luego restar las coordenadas `y`, elevar el resultado al cuadrado; sumar ambos resultados y finalmente sacar la raíz cuadrada. ¡Así de fácil!
Distancia en espacios especiales
Distancia en una superficie curva
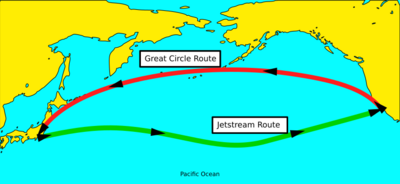
La distancia en línea recta no siempre es útil. Por ejemplo, en la superficie de la Tierra, no podemos cavar un túnel recto de un continente a otro. En su lugar, medimos el camino más corto a lo largo de la superficie, como el "camino a vuelo de pájaro". Esto se calcula usando la distancia ortodrómica en una esfera.
En general, el camino más corto entre dos puntos en una superficie curva se llama geodésica. Piensa en una hormiga caminando sobre una pelota: la geodésica sería el camino más corto que la hormiga podría tomar sin volar.
Efectos de la relatividad
En la teoría de la relatividad, las distancias entre objetos pueden cambiar dependiendo de cómo se estén moviendo las personas que las miden. A escalas muy grandes, como entre galaxias, la expansión del universo también afecta cómo medimos las distancias.
Otras formas de medir distancias en el espacio
A veces, las definiciones de distancia pueden ser un poco diferentes para modelar situaciones específicas:
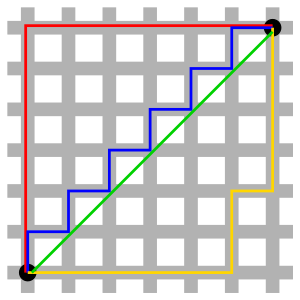
- La distancia de Manhattan (o distancia del taxista) se usa en ciudades con calles en forma de cuadrícula. Es la distancia que recorrerías si solo pudieras moverte en líneas horizontales y verticales, como un taxi.
- La distancia de Chebyshov (o distancia del tablero de ajedrez) es el número mínimo de movimientos que un rey de ajedrez necesita para ir de una casilla a otra.
Distancias que no son físicas
La idea de distancia no solo se usa para medir el espacio. También se usa para comparar qué tan diferentes son dos cosas.
Distancias en estadística
En estadística, las "distancias estadísticas" miden qué tan diferentes son dos grupos de datos o probabilidades. Ayudan a entender cómo se relacionan los datos.
Distancias de edición
En informática, una "distancia de edición" mide qué tan diferentes son dos palabras o textos. Por ejemplo, las palabras "casa" y "masa" están muy cerca porque solo cambia una letra. Esta idea se usa en los correctores ortográficos para sugerir palabras correctas.
Distancia en teoría de grafos
En la teoría de grafos (que estudia redes de puntos y líneas), la distancia entre dos puntos (llamados vértices) es la longitud del camino más corto que los conecta. Por ejemplo, en una red social, la idea de "seis grados de separación" significa que la distancia entre dos personas cualesquiera es, como máximo, seis conexiones.
Distancia en las ciencias sociales
En psicología y sociología, la distancia a veces se refiere a qué tan "alejado" se siente algo de una persona, o qué tan separados están los individuos o grupos sociales en la sociedad por diferencias como la clase social, raza o género.
¿Qué es una función de distancia?
La mayoría de las formas de medir la distancia que hemos visto son ejemplos de una idea matemática llamada "métrica" o "función de distancia". Una función de distancia es una regla que asigna un número a cada par de puntos u objetos, y debe cumplir estas reglas:
- La distancia de un objeto a sí mismo siempre es cero.
- La distancia entre objetos diferentes siempre es un número positivo.
- La distancia es igual en ambas direcciones: de A a B es lo mismo que de B a A.
- La desigualdad triangular: si vas de A a C, no puedes llegar más rápido pasando por un punto intermedio B. Es decir, el camino directo es siempre el más corto o igual de corto que cualquier camino con paradas.
Galería de imágenes
Véase también
 En inglés: Distance Facts for Kids
En inglés: Distance Facts for Kids