Theorema egregium para niños
El Theorema Egregium (que significa "teorema destacable" en latín) es una idea muy importante en el estudio de las formas y superficies, dentro de una rama de las matemáticas llamada geometría diferencial. Fue descubierto por un gran matemático llamado Carl Friedrich Gauss.
Este teorema nos dice algo sorprendente sobre cómo medimos la "curvatura" de una superficie. Imagina que estás en la superficie de una pelota o de una hoja de papel. El Theorema Egregium explica que puedes saber qué tan curva es esa superficie solo haciendo mediciones sobre ella misma, como midiendo distancias y ángulos. No necesitas salir de la superficie para ver cómo se dobla en el espacio. Es como si la curvatura fuera una característica "interna" de la superficie.
Contenido
¿Por qué es "destacable" o "sorprendente"?
Gauss llamó a este teorema "egregium" (destacable) porque la forma en que se define la curvatura de una superficie normalmente requiere saber cómo esa superficie se encuentra en el espacio. Por eso, era muy sorprendente descubrir que el resultado final de la curvatura no depende de cómo la superficie está colocada o doblada en el espacio tridimensional.
En palabras más sencillas, el teorema dice que si puedes "desdoblar" o "estirar" una superficie curva sobre otra sin arrugarla ni romperla, entonces la medida de su curvatura en cada punto se mantiene igual.
Ejemplos y aplicaciones del Theorema Egregium
El Theorema Egregium tiene consecuencias muy interesantes y útiles en la vida real.
¿Por qué los mapas no son perfectos?
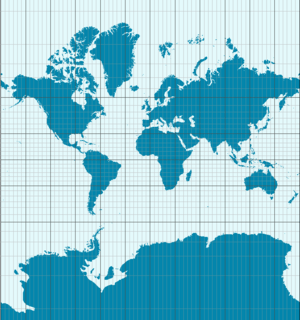
- Imagina una esfera, como la Tierra, y una hoja de papel plana. Una esfera tiene una curvatura constante, mientras que un plano no tiene curvatura. El teorema nos dice que no puedes aplanar la superficie de una esfera en una hoja de papel sin que se arrugue, se estire o se rompa. Esto significa que es imposible hacer un mapa plano de la Tierra que sea perfectamente exacto en todas sus partes. Todos los mapas planos tienen alguna distorsión en las distancias o en las áreas.
Formas que se transforman
- Existen dos formas matemáticas llamadas catenoide y helicoide. Aunque se ven muy diferentes, el Theorema Egregium nos dice que se pueden transformar una en la otra sin cambiar su curvatura interna. Esto es porque, matemáticamente, son "iguales" en cuanto a su curvatura.
Superficies que se pueden "desenrollar"
- Algunas superficies, como un cilindro o un cono, tienen una curvatura especial que es cero. Esto significa que puedes construirlas fácilmente a partir de una hoja de cartón plana, simplemente enrollándola o doblándola. Esto es posible porque su curvatura interna es la misma que la de una superficie plana.
Véase también
 En inglés: Theorema Egregium Facts for Kids
En inglés: Theorema Egregium Facts for Kids
- Curvatura gaussiana


