Cálculo infinitesimal para niños
El cálculo es una rama muy importante de las matemáticas. Así como la geometría estudia las formas y el álgebra trabaja con símbolos y ecuaciones, el cálculo se dedica a entender el cambio y la continuidad. Piensa en cómo algo cambia poco a poco, sin saltos.
El cálculo se divide en dos partes principales: el cálculo diferencial y el cálculo integral. El cálculo diferencial nos ayuda a saber cómo cambia una función en un punto específico. Es como calcular la velocidad de algo en un instante. La operación principal aquí se llama «derivada». El cálculo integral, por otro lado, hace lo contrario. Nos permite sumar muchos cambios pequeños para encontrar el total, como calcular el área bajo una curva o el volumen de una figura.
Desde que apareció en el siglo XVII, el cálculo ha sido fundamental para la ciencia y la ingeniería. Fue clave en la Revolución científica y se usa para resolver problemas que antes eran imposibles. Por ejemplo, ayuda a encontrar la línea que toca una curva en un solo punto, a medir áreas y volúmenes de formas irregulares, o a entender si una suma de números que nunca termina llega a un valor fijo.
Hoy en día, el cálculo es una parte esencial de la educación en muchas carreras universitarias. También es la base de una rama más avanzada de las matemáticas llamada análisis matemático.
Historia del Cálculo
El cálculo tiene raíces muy antiguas, con ideas que surgieron en diferentes culturas mucho antes de su forma moderna.
Ideas Antiguas del Cálculo
Algunas ideas del cálculo integral se vieron en el Antiguo Egipto. Por ejemplo, en los papiros matemáticos de Moscú (alrededor del 1890 a. C.), se calculó el volumen de una pirámide truncada. Los babilonios también pudieron haber usado una forma temprana de la regla trapezoidal para sus observaciones del planeta Júpiter.
En la Antigua Grecia, matemáticos como Eudoxo de Cnido (408-355 a. C.) usaron el «método exhaustivo» para calcular áreas y volúmenes. Este método es parecido a la idea de límite que se usa hoy. Más tarde, Arquímedes (287-212 a. C.) mejoró esta idea con un método que se parece mucho al cálculo.
En China, en el siglo III, Liu Hui usó el método exhaustivo para encontrar el área de un círculo. En el siglo V, Zu Chongzhi usó una idea similar, llamada más tarde la teoría de los indivisibles, para calcular el volumen de una esfera.
Avances en la Edad Media
En el siglo XI, el matemático islámico Alhacén encontró una fórmula para sumar potencias, lo que fue un paso importante. El científico chino Shen Kuo también desarrolló ecuaciones relacionadas con la integración.
En el siglo XII, el matemático indio Bhaskara II trabajó con cambios muy pequeños, lo que se parece a una derivada temprana. También el matemático persa Sharaf al-Din al-Tusi descubrió la derivada de una función cúbica, un avance en el cálculo diferencial.
En el siglo XIV, la Escuela de Kerala en la India describió casos especiales de las series de Taylor, que son muy importantes en el cálculo.
El Cálculo Moderno
En Europa, el cálculo moderno empezó a tomar forma en el siglo XVII. El matemático italiano Bonaventura Cavalieri propuso que los volúmenes y áreas podían calcularse sumando secciones muy delgadas.
Los matemáticos John Wallis, Isaac Barrow y James Gregory combinaron estas ideas. Barrow y Gregory demostraron el teorema fundamental del cálculo alrededor de 1675.
Isaac Newton y Gottfried Wilhelm Leibniz son considerados los inventores del cálculo moderno. Newton usó el cálculo para resolver problemas de física, como el movimiento de los planetas y la forma de la Tierra. Él desarrolló ideas como la derivada y las series de Taylor.
Leibniz, por su parte, creó un sistema de reglas claras para trabajar con cantidades muy pequeñas y desarrolló gran parte de la notación que usamos hoy en día en cálculo. Aunque hubo una gran discusión sobre quién lo inventó primero, hoy se reconoce que ambos llegaron a sus descubrimientos de forma independiente. Newton fue el primero en aplicar el cálculo a la física, y Leibniz desarrolló la notación.
Desde entonces, muchos matemáticos han contribuido al cálculo, haciéndolo más preciso y general. En el siglo XIX, matemáticos como Cauchy, Riemann y Weierstrass le dieron una base más sólida.
¿Qué es el Cálculo?
Límites y Cantidades Pequeñas
El cálculo trabaja con la idea de cantidades muy, muy pequeñas, llamadas infinitesimales. Imagina un número que es más grande que cero, pero más pequeño que cualquier fracción que puedas pensar (como 1/2, 1/3, 1/4...). Históricamente, el cálculo usaba estos infinitesimales.
Más tarde, los matemáticos usaron el concepto de «límite». Un límite describe cómo se comporta una función cuando te acercas mucho a un punto, sin necesidad de llegar a él. Es como ver qué pasa con la velocidad de un coche justo antes de que se detenga. Los límites dieron una base más sólida al cálculo.
Cálculo Diferencial: El Estudio del Cambio
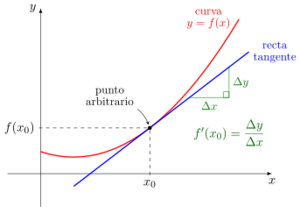
El cálculo diferencial estudia la derivada de una función. La derivada nos dice qué tan rápido cambia algo. Piensa en la pendiente de una línea recta: la derivada es como la pendiente de una línea que toca una curva en un solo punto. Esta línea se llama recta tangente.
El proceso de encontrar la derivada se llama derivación o diferenciación. Si tienes una función que te dice la posición de una pelota en cada momento, su derivada te dirá la velocidad de la pelota en ese instante.
Por ejemplo, si la posición de algo se describe con la función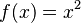 
, su derivada es Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): f'(x) = 2x . Esto significa que la velocidad o el cambio de 
en cualquier punto 
es 
.
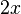Cálculo Integral: Sumando Pequeños Cambios
El cálculo integral se ocupa de dos ideas relacionadas: la integral indefinida y la integral definida. El proceso de encontrar una integral se llama integración.
La integral indefinida es lo contrario de la derivada. Si la derivada de una función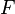 
es 
, entonces 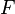es la integral indefinida de . Es como deshacer lo que hizo la derivada.
La integral definida nos ayuda a calcular el área entre una curva en un gráfico y el eje horizontal. Imagina que divides esa área en muchos rectángulos muy delgados y luego sumas sus áreas. La integral definida es el resultado de esa suma cuando los rectángulos se hacen infinitamente delgados.
El Teorema Fundamental del Cálculo
El teorema fundamental del cálculo es una idea muy importante que conecta el cálculo diferencial y el integral. Dice que la diferenciación y la integración son operaciones inversas. Es decir, una deshace lo que hace la otra.
Este teorema hace que sea mucho más fácil calcular integrales definidas, porque en lugar de sumar infinitos rectángulos, podemos usar la antiderivada de la función. Fue un descubrimiento clave para el avance de las matemáticas.
Aplicaciones del Cálculo
El cálculo se usa en casi todas las áreas de la ciencia, la ingeniería, la economía, la medicina y muchas otras. Es una herramienta poderosa para entender cómo cambian las cosas y cómo interactúan.
En la Física
La física usa el cálculo de forma extensiva:
- En la mecánica clásica, el cálculo relaciona conceptos como la posición, la velocidad y la aceleración. Por ejemplo, la segunda ley de Newton (Fuerza = masa × aceleración) usa el cálculo, porque la aceleración es la derivada de la velocidad.
- El electromagnetismo y la mecánica cuántica también se describen con ecuaciones que usan cálculo.
- La teoría de la relatividad general de Albert Einstein se basa en el cálculo.
En Química e Ingeniería
- En ingeniería eléctrica y electrónica, el cálculo es esencial para entender cómo funcionan los circuitos eléctricos con componentes como capacitores e inductores.
- La química lo usa para calcular la velocidad de las reacciones químicas o el tiempo que tarda una sustancia radioactiva en descomponerse.
En Ciencias Biológicas
- En biología, el cálculo ayuda a modelar cómo se desarrollan los organismos o cómo cambian las poblaciones de animales.
- En neurociencia, las ecuaciones que explican cómo las neuronas envían señales usan el cálculo.
- En la medicina, se puede usar para calcular la dosis correcta de un medicamento o para planificar tratamientos de radioterapia.
En Ciencias Sociales
- En demografía y ecosistemas, los modelos que predicen el crecimiento de la población se basan en el cálculo.
- En epidemiología, se usan modelos de cálculo para predecir cómo se propagan las enfermedades.
- En economía, el cálculo ayuda a determinar el punto donde se obtiene la mayor ganancia o la menor pérdida.
En Otras Ramas de las Matemáticas
El cálculo se combina con otras áreas de las matemáticas:
- Con el álgebra lineal, ayuda a encontrar la mejor aproximación para un conjunto de puntos.
- En la teoría de la probabilidad, se usa para calcular la probabilidad de eventos continuos.
- En geometría analítica, el cálculo sirve para encontrar los puntos más altos o más bajos de una curva, o dónde cambia de dirección.
- También se usa para encontrar soluciones aproximadas a ecuaciones complejas, como las que usan las naves espaciales para calcular sus trayectorias.
Véase también
En inglés: Calculus Facts for Kids
- Derivada
- Diferencial
- Integral
- Gottfried Leibniz
- Isaac Newton
- Seki Kōwa
- Máquina diferencial
