Teorema fundamental del cálculo para niños
El teorema fundamental del cálculo es una idea muy importante en las matemáticas. Nos dice que la derivación y la integración de una función son como operaciones opuestas. Imagina que una operación "deshace" lo que la otra hace. Esto significa que si calculas la integral de una función y luego la derivas, ¡vuelves a tener la función original! Este teorema es clave en una parte de las matemáticas llamada análisis matemático o cálculo infinitesimal.
Antes de este teorema, calcular áreas (integración) y estudiar cómo cambian las cosas (derivación) eran dos ramas de las matemáticas que se trabajaban por separado. Matemáticos como Arquímedes ya calculaban áreas hace mucho tiempo. Por otro lado, el cálculo diferencial se estaba desarrollando con científicos como Isaac Newton, Isaac Barrow y Gottfried Leibniz en el siglo XVII. El teorema fundamental del cálculo unió estas dos ideas, mostrando que el cálculo del "área bajo una función" está muy relacionado con cómo cambian las funciones. Así, la integración se convirtió en la operación inversa de la derivación.
Una consecuencia directa de este teorema es la regla de Barrow, a veces llamada el segundo teorema fundamental del cálculo. Esta regla nos ayuda a calcular fácilmente el valor de una integral definida usando las funciones originales.
Contenido
¿Qué es el Teorema Fundamental del Cálculo?
El teorema fundamental del cálculo nos enseña que dos operaciones matemáticas, la derivación y la integración, están conectadas de una manera especial. Son como el "sumar" y "restar" o "multiplicar" y "dividir" en matemáticas básicas.
¿Qué es la Derivación?
La derivación nos ayuda a entender cómo cambia una función en un punto específico. Por ejemplo, si tienes una función que describe la posición de un coche, su derivada te dirá la velocidad del coche en cada momento.
¿Qué es la Integración?
La integración, por otro lado, nos permite calcular el área bajo la curva de una función. Imagina que tienes un gráfico y quieres saber cuánto espacio hay entre la línea de la función y el eje horizontal. La integración te da esa medida.
Un Poco de Historia: ¿Quién lo Descubrió?
Este teorema fue un gran avance porque, antes de él, nadie se había dado cuenta de que la derivación y la integración estaban tan relacionadas.
Los Primeros Pasos
Desde la Antigua Grecia, matemáticos como Arquímedes ya sabían cómo calcular áreas usando ideas parecidas a la integración. También, mucho antes del teorema, ya se estudiaban conceptos como la "continuidad" de las funciones y el "movimiento" en el siglo XIV.
Los Grandes Descubridores
La conexión entre estas dos operaciones fue descubierta y desarrollada por varios matemáticos.
- James Gregory (1638–1675) fue el primero en publicar una versión del teorema.
- Isaac Barrow (1630–1677) demostró una versión más general.
- Su alumno, Isaac Newton (1642–1727), completó el desarrollo de la teoría.
- Gottfried Leibniz (1646–1716) organizó todo este conocimiento y creó la notación que usamos hoy en día para el cálculo.
La importancia histórica del teorema no es solo que nos permite hacer cálculos, sino que nos mostró que dos operaciones que parecían muy diferentes (calcular áreas y calcular velocidades) ¡estaban en realidad muy unidas!
Entendiendo el Teorema con Geometría
Para entender mejor el teorema, podemos usar un ejemplo con áreas.
Imagina que tienes una función continua 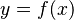 que dibujas como una curva. Para cada valor de
que dibujas como una curva. Para cada valor de  , podemos pensar que hay una función
, podemos pensar que hay una función 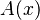 que representa el área bajo la curva desde un punto inicial (como el 0) hasta
que representa el área bajo la curva desde un punto inicial (como el 0) hasta  .
.
Ahora, queremos calcular el área bajo la curva entre dos puntos:  y
y  . Podemos hacerlo restando el área hasta
. Podemos hacerlo restando el área hasta  del área hasta
del área hasta  . Es decir, el área sería
. Es decir, el área sería 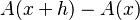 .
.
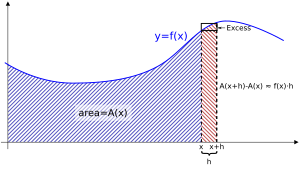
Otra forma de estimar esta misma área es multiplicar 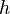 (el ancho) por
(el ancho) por  (la altura). Esto nos da el área de un rectángulo que se parece mucho a la "rebanada" de área que buscamos. Cuanto más pequeño sea el valor de
(la altura). Esto nos da el área de un rectángulo que se parece mucho a la "rebanada" de área que buscamos. Cuanto más pequeño sea el valor de 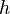 , más precisa será esta estimación.
, más precisa será esta estimación.
Entonces, podemos decir que 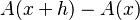 es casi igual a
es casi igual a 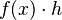 . Esta aproximación se vuelve una igualdad perfecta cuando
. Esta aproximación se vuelve una igualdad perfecta cuando 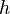 se acerca mucho a cero.
se acerca mucho a cero.
Si dividimos ambos lados de la ecuación por 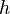 , obtenemos:
, obtenemos: 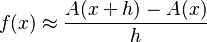
Cuando 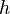 se acerca a cero, la parte derecha de la ecuación es la definición de la derivada de la función
se acerca a cero, la parte derecha de la ecuación es la definición de la derivada de la función 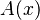 , que se escribe como
, que se escribe como 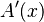 . Y la parte izquierda se queda como
. Y la parte izquierda se queda como  .
.
Esto nos muestra que  . En otras palabras, la derivada de la función que calcula el área (
. En otras palabras, la derivada de la función que calcula el área (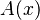 ) es la función original (
) es la función original ( ). Esto significa que la función de área
). Esto significa que la función de área 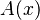 es la "antiderivada" de la función original.
es la "antiderivada" de la función original.
 |
De forma sencilla, esto demuestra que calcular la derivada de una función y "hallar el área" bajo su curva son operaciones "inversas". ¡Esa es la idea principal del teorema fundamental del cálculo!
Primer Teorema Fundamental del Cálculo
Este teorema nos dice que si tenemos una función continua  en un intervalo
en un intervalo ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) , y definimos una nueva función
, y definimos una nueva función 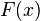 como el área bajo
como el área bajo  desde
desde  hasta
hasta  , entonces la derivada de
, entonces la derivada de 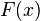 es la función original
es la función original  .
.
Teorema
Si  es una función continua en el intervalo
es una función continua en el intervalo ![[a,b],](/images/math/f/1/2/f12644f1c0d00b07716732c25819450c.png) y definimos
y definimos 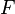 en
en ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) como:
como:
Entonces, 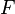 es derivable en cualquier punto
es derivable en cualquier punto  dentro del intervalo
dentro del intervalo 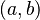 y su derivada es:
y su derivada es:
Ejemplos
Aquí tienes algunos ejemplos para entender cómo funciona:
Ejemplo 1
Si tenemos la función Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F(x) = \int_{0}^{x} t^2 dt , que representa el área bajo la curva Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): t^2 desde 0 hasta  . Según el teorema, la derivada de
. Según el teorema, la derivada de 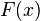 es simplemente la función original evaluada en
es simplemente la función original evaluada en  : Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F'(x) = x^2
: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): F'(x) = x^2
Ejemplo 2
Si tenemos Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H(x) = \int_{0}^{e^{3x}} \sen(t) dt . Aquí, el límite superior de la integral es una función de  (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{3x} ). Para encontrar la derivada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H'(x) , aplicamos el teorema y la regla de la cadena:
(Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{3x} ). Para encontrar la derivada Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): H'(x) , aplicamos el teorema y la regla de la cadena:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} H'(x) &=\sen\left(e^{3x}\right) \cdot \text{derivada de } (e^{3x}) \\ &=\sen\left(e^{3x}\right) e^{3x} \cdot3 \\ &=3e^{3x}\sen\left(e^{3x}\right) \end{align}
Segundo Teorema Fundamental del Cálculo
El segundo teorema fundamental del cálculo integral (también conocido como la regla de Barrow o regla de Newton-Leibniz) es muy útil. Nos permite calcular fácilmente el valor de una integral definida si conocemos una "función primitiva" de la función original. Una función primitiva es una función cuya derivada es la función original.
Teorema
Si  es una función continua en el intervalo
es una función continua en el intervalo ![[a,b]](/images/math/2/c/3/2c3d331bc98b44e71cb2aae9edadca7e.png) y
y 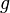 es una función primitiva de
es una función primitiva de  (es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g'=f ), entonces:
(es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g'=f ), entonces:
Esto significa que para calcular el área bajo  desde
desde  hasta
hasta  , solo necesitas encontrar una función
, solo necesitas encontrar una función 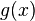 cuya derivada sea
cuya derivada sea  , y luego restar el valor de
, y luego restar el valor de 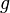 en
en  del valor de
del valor de 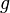 en
en  .
.
Ejemplos
Veamos cómo se usa este teorema:
Ejemplo 1
Queremos calcular la integral:
Sabemos que la derivada de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen(x) es 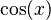 . Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x)=\sen(x) es una función primitiva de
. Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x)=\sen(x) es una función primitiva de 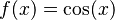 . Aplicando el teorema:
. Aplicando el teorema:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \int_0^{\pi} \cos(x)dx &=\sen(\pi)-\sen(0) \\ &=0-0 \\ &=0 \end{align}
Ejemplo 2
Queremos calcular la integral:
Sabemos que la derivada de 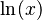 (logaritmo natural de x) es
(logaritmo natural de x) es 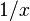 . Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x)=\ln(x) es una función primitiva de
. Así que, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): g(x)=\ln(x) es una función primitiva de  . Aplicando el teorema:
. Aplicando el teorema:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{align} \int_1^e \frac{dx}{x} &=\ln(e)-\ln(1) \\ &=1-0 \\ &=1 \end{align}
Galería de imágenes
Véase también


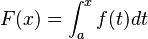
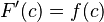

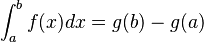
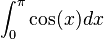
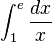

 En inglés:
En inglés: