Metro para niños
Datos para niños Metro |
||
|---|---|---|
 |
||
| Estándar | Unidades básicas del Sistema Internacional | |
| Magnitud | Longitud | |
| Símbolo | m | |
| Equivalencias | ||
| Unidades de Planck | 1 m = 6,19·1034 | |
| Pulgadas | 1 m = 39,37" | |
| Centímetros | 1 m = 100 cm | |
El metro (símbolo: m) es la unidad coherente de longitud del Sistema Internacional de Unidades. Se define como la distancia que recorre la luz en el vacío en un intervalo de 1/299 792 458 s.
El metro se definió originalmente en 1793 como una diez millonésima parte de la distancia desde el Ecuador hasta el polo norte a lo largo de un gran círculo, por lo que la circunferencia de la Tierra es aproximadamente 40 000 kilómetros. En 1799, el medidor se redefinió en términos de una barra de medidor prototipo (la barra real utilizada se cambió en 1889). En 1960, el medidor se redefinió en términos de un cierto número de longitudes de onda de una cierta línea de emisión de kriptón-86. La definición actual se adoptó en 1983 y se modificó ligeramente en 2002 para aclarar que el metro es una medida de longitud adecuada .
Contenido
Historia del metro y sus definiciones
La palabra metro proviene del griego μέτρον (metron, medida); de aquí pasó al francés como mètre. Su utilización en el sentido moderno de unidad de medida fue introducida por el científico italiano Tito Livio Burattini en su obra Misura Universale de 1675 para cambiar de nombre a metro cattolico la medida universal propuesta por el filósofo inglés John Wilkins en 1668.
En 1668 Wilkins hizo su propuesta de medida universal utilizando la sugerencia de Christopher Wren de un péndulo con un semiperiodo de un segundo para medir una longitud estándar de 997 mm de longitud que había observado Christiaan Huygens.
Durante el siglo XVIII hubo dos tendencias predominantes respecto a la definición de la unidad estándar de longitud. Una de estas, siguiendo a Wilkins, sugería la definición del metro como la longitud de un péndulo con un semiperíodo de un segundo. Mientras tanto, la otra proponía una definición basada en la longitud del meridiano terrestre entre el ecuador y el polo norte: la diezmillonésima parte de la longitud de la mitad del meridiano terrestre. En 1791, la Academia de Ciencias de Francia optó por la segunda definición frente a la que se basaba en el péndulo porque la fuerza de la gravedad varía significativamente a lo largo de la superficie de la Tierra y esta variación afecta el periodo del péndulo.
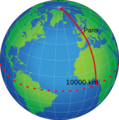
El metro fue definido en 1791 por la Academia Francesa de las Ciencias como la diezmillonésima parte del cuadrante de un meridiano terrestre; concretamente, la distancia a través de la superficie de la Tierra desde el polo norte hasta el ecuador pasando por el meridiano de París (más precisamente por el observatorio de París). Este meridiano ya había sido medido con anterioridad en 1669 por Jean Picard (tramo París-Amiens), alargado hasta Dunkerque y Perpiñán en 1718 por Jean-Dominique Cassini (Giovanni Cassini) y revisado en 1739 por LaCaille. La Academia de Ciencias creó una comisión formada por Borde, Condorcet, Lagrange, Lavoisier, Tillet añadiéndose posteriormente Laplace y Monge que encargó a Pierre-François André Méchain (1744-1804) y Jean-Baptiste Joseph Delambre (1749-1822) efectuar las medidas geodésicas pertinentes para calcular el arco del meridiano y poder deducir la longitud del metro. La tarea de medida se alargó del 1792 al 1798, entre otras razones debido a las Guerras revolucionarias francesas. Estas medidas se llevaron a cabo en una primera fase entre Dunkerque y Barcelona. En concreto, el meridiano de París llega al mar en la playa de Ocata, en el Masnou. En una segunda fase, las medidas se prolongaron hasta las Islas Baleares, entre los años 1806 y 1808. El científico norte-catalán Francesc Aragón, que explica en sus memorias que conoció a Méchain cuando este medía el arco de meridiano por el Rossellón, fue uno de los miembros de la segunda expedición que completó, alargándolas hacia Alicante, Ibiza y Mallorca, las medidas que permitieron confirmar esta primera definición. Al estallar la guerra del Francés, Francesc Aragón evitó situaciones problemáticas gracias a su conocimiento del catalán, pero tuvo que refugiarse en la prisión del castillo de Bellver con sus ayudantes, y no pudieron volver a Francia sino hasta un año más tarde. En 1795, Francia adoptó el metro como unidad oficial de longitud.
A lo largo de toda la historia, se llevaron a cabo intentos de unificación de las distintas medidas con el objetivo de simplificar los intercambios, facilitar el comercio y el cobro justo de impuestos. En la Revolución francesa de 1789, junto a otros desafíos considerados necesarios para los nuevos tiempos, se nombraron Comisiones de Científicos para uniformar los pesos y medidas, entre ellos está la longitud. La tarea fue ardua y complicada; se barajó como un patrón de la longitud de un péndulo de segundos a una latitud de 45°, pero acabaría descartándose por no ser un modelo completamente objetivo; se acordaría, por fin, medir un arco de meridiano para establecer, sobre él y por tanto sobre la propia Tierra, el patrón del metro. Los encargados de dicha medida fueron Jean-Baptiste Joseph Delambre y Pierre Méchain, quienes entre 1791 y 1798 y mediante un sistema de triangulación desde Dunkerque a Barcelona establecieron la medida de dicho arco de meridiano sobre la que se estableció el metro. Contaron con la colaboración del matemático y astrónomo español José Chaix Isniel, quien fue comisionado por el gobierno de España entre 1791 y 1793 para colaborar con el proyecto dirigido por Méchain.
Definición de 1792
Inicialmente esta unidad de longitud fue creada por la Academia de Ciencias de Francia en 1792 y definida como la diezmillonésima parte de la distancia que separa el polo norte de la línea del ecuador terrestre, a través de la superficie terrestre.
Nuevo patrón de 1889
El 28 de septiembre de 1889, la Comisión Internacional de Pesos y Medidas adoptó nuevos prototipos para el metro y, después, para el kilogramo, los cuales se materializaron en un metro patrón de platino e iridio depositados en cofres situados en los subterráneos del pabellón de Breteuil en Sèvres, Oficina de Pesos y Medidas, en las afueras de París.
Definición de 1960
La 11.ª Conferencia de Pesos y Medidas adoptó una nueva definición del metro: «1 650 763,73 veces la longitud de onda en el vacío de la radiación naranja del átomo del criptón 86». La precisión era cincuenta veces superior a la del patrón de 1889. (Equivalencias: una braza = 2,09 m; un palmo = 0,2089 m).
Definición en término de la rapidez de la luz
Esta es la actual definición, se adoptó en 1983 por la 17.ª Conferencia General de Pesas y Medidas. Se define como la distancia que recorre la luz en el vacío en un intervalo de 1/299 792 458 s. Fijó la longitud del metro en función de segundos y de la velocidad de la luz:
El metro es la longitud del trayecto recorrido por la luz en el vacío durante un intervalo de tiempo de 1⁄299,792,458 segundos.
Esta definición fija la velocidad de la luz en el vacío en exactamente a 299 792 458 m/s (metros por segundo). Una subproducto de la definición de la 17.ª CGPM fue que permitió a los científicos comparar sus láseres cuidadosamente utilizando frecuencia, el que resulta en longitudes de onda con una quinta parte de la incertidumbre involucrado en la comparación directa de longitudes de onda, gracias al hecho que los de errores de interferómetros fueron eliminados. Para facilitar todavía más la reproducibilidad de un laboratorio a la 17.ª CGPM también hizo la helio-neón láser de yodo estabilizado, «una radiación recomendada» para la realización del metro. Con el fin de delinear el metro, el BIPM actualmente considera la longitud de onda láser de HeNe tiene que ser de la siguiente manera: λHeNe = 632,991,212.58 fm con una incertidumbre estándar relativa estimada (U) de 2,1×10−11. Esta incertidumbre es actualmente un factor limitante en realizaciones de laboratorio del metro, y que es varios órdenes de magnitud más pobre que el de la segunda, con base en reloj atómico de fuente de cesio (1=U = 5×10−16). Por lo tanto, una realización del metro normalmente es delineado (no definido) hoy en día a los laboratorios como 1.579.800,762042(33) longitudes de onda de la luz láser de helio-neón en el vacío, el error indicado es solamente la de determinación de la frecuencia. Esta notación en claves expresando el error se explica en el artículo sobre la incertidumbre de medida.
La realización práctica del metro está sujeta a incertidumbres en la caracterización del medio, a varias incertidumbres de interferometría, y a la incertidumbre en la medida de la frecuencia de la fuente. Un medio utilizado de forma habitual es aire, y el Instituto Nacional de Estándares y Tecnología ha creado una calculadora en línea para convertir las longitudes de onda en el vacío en longitudes de onda en el aire. Según la descripción realizada por el NIST, en el aire, las incertidumbres en la caracterización de la media están dominadas por los errores en la búsqueda de la temperatura y la presión. Los errores en las fórmulas teóricas utilizadas son secundarios. Al implementar una corrección del índice de refracción de este tipo, una aproximación de la realización del metro puede ser implementada al aire, como por ejemplo, el uso de la formulación del metro como 1.579.800,762042(33) longitudes de onda de la luz láser de helio-neón en el vacío, y convertir las longitudes de onda en el vacío a longitudes de onda en el aire. Por supuesto, el aire es sólo un posible medio a utilizar en una realización del metro, y cualquier vacío parcial puede ser utilizado, o alguna atmósfera inerte como el gas helio, siempre que las correcciones apropiadas para el índice de refracción se implementen.
Unidad de longitud en metros
Aunque la medida actualmente está definida como la longitud del camino recorrido por la luz en un tiempo dado, las mediciones de la longitud practicados al laboratorio en metros se determinó contando el número de longitudes de onda de la luz láser de uno de los tipo estándar que se ajustan a la longitud, y la conversión de la unidad seleccionada de longitud de onda a metros. Hay tres factores principales que limitan la precisión alcanzable con láser interferómetros para una medida de longitud:
- La incertidumbre en la longitud de onda de la fuente de vacío,
- La incertidumbre en el índice de refracción del medio,
- Valor mínimo de la resolución del interferómetro.
De estos, el último es peculiar del mismo interferómetro. La conversión de una longitud en longitudes de onda a una longitud en metros se basa en la relación:
que convierte la unidad de longitud de onda 
en metros a c, la velocidad de la luz en el vacío, en m/s. Aquí n es el índice de refracción del medio en que se realiza la medición, y f es la frecuencia de medida de la fuente. A pesar de que la conversión de longitudes de onda a metros introduce un error adicional en la longitud total debido a errores de medida en la determinación del índice de refracción y la frecuencia, la medida de la frecuencia es una de las medidas más precisas disponibles.
Evolución de la definición del metro
- 8 de mayo del 1790: la Asamblea Nacional Francesa decidió que la longitud del nuevo metro tiene que ser igual a la longitud de uno péndulo con un semiperiodo de un segundo.
- 26 de marzo del 1791: la Asamblea Nacional Francesa acepta la propuesta de la Academia de Ciencias de Francia y decreta que la nueva definición del metro sea igual a una diezmillonésima parte de la longitud de un cuarto del meridiano terrestre. A partir de entonces empezará a medir un arco de meridiano entre Dunkerque y Barcelona que serviría de base a la nueva definición del metro.
- 1795: en el mes de julio se construye un patrón provisional en latón y es enviado al Comité de Instrucción Pública.
- 10 de diciembre del 1799: la Asamblea Nacional Francesa establece por ley el prototipo del metro como patrón de las medidas de longitud a la República. El prototipo definitivo había sido presentado lo 22 de junio del 1799, era uno reglo plan construido en platino y de sección rectangular, este primer prototipo definitivo fue depositado al Archivo Nacional de Francia.
- 28 de septiembre del 1889: la primera Conferencia General de Pesas y Medidas (CGPM) que se celebra en París, define el metro como la distancia entre dos líneas marcadas en una barra de platino con el 10 % de iridio medida en a la temperatura de fusión del hielo.
- 6 de octubre del 1927: la 7.ª CGPM ajusta la definición del metro como la distancia a 0 °C entre los ejes de dos líneas centrales marcadas sobre la barra de platino-iridio del prototipo, con la barra sometida a unas condiciones estándares de presión atmosférica y soportada por dos cilindros de como mínimo un centímetro de diámetro puestos de manera simétrica al mismo plan horizontal y a una distancia de 571 mm (milímetros) entre ambos.
- 20 de octubre del 1960: la 11.ª CGPM definió el metro como 1 650 763,73 veces la longitud de onda en el vacío de la radiación que corresponde a la transición entre los niveles cuánticos 2p10 y 5d5 de la átomo de kriptón-86.
- 21 de octubre del 1983: la 17.ª reunión de la CGPM estableció la definición actual del metro, la longitud recorrida por la luz en el vacío en uno tiempo de 1/299.792.458 segundos. Esta definición tiene la ventaja que la velocidad de la luz al vacío es una constante física fundamental, cosa que hace la definición del metro independiente de cualquier objeto material de referencia.
| Base de la definición | Fecha | Incertidumbre absoluta |
Incertidumbre relativa |
|---|---|---|---|
| 1⁄10,000,000 parte de la cuarta parte de una medida astronómica meridiano de Bessel (443,44 líneas) | 1792 | 0.5-0.1 mm (milímetros) | 10−4 |
| 1⁄10,000,000 parte de la cuarta parte de un meridiano , medida por Delambre y Méchain (443,296 líneas) | 1795 | 0.5-0.1 mm | 10−4 |
| Primer prototipo delMetro des Archives, la barra de platino estándar | 1799 | 0.05-0.01 mm | 10−5 |
| Barra de platino-iridio en su punto de fusión del hielo (1.ª CGPM) | 1889 | 0.2-0.1 µm (micrómetros) | 10−7 |
| Barra de platino-iridio en su punto de fusión del hielo, presión atmosférica, apoyada por dos rodillos (7.ª CGPM) | 1927 | n.a. | n.a. |
| Transición atómica hiperfina; 1,650,763.73 longitudes de onda de la luz de una transición especificado en kriptón-86 (11.ª CGPM) | 1960 | 0.01-0.005 µm | 10−8 |
| Longitud de la trayectoria recorrida por la luz en el vacío en 1⁄299,792,458 de segundo (17.ª CGPM) | 1983 | 0.1 nm | 10−10 |
Ortografía
Metre es la grafía estándar de la unidad métrica de longitud en casi todas las naciones de habla inglesa, excepto en Estados Unidos y Filipinas, que utilizan metro. Otras lenguas germánicas, como el alemán, el neerlandés y las lenguas escandinavas, también escriben la palabra meter.
Los aparatos de medición (como amperímetro, velocímetro) se escriben -meter en todas las variantes del inglés. El sufijo «-metro» tiene el mismo origen griego que la unidad de longitud.
Etimología
La palabra metro proviene del término griego μέτρον (metron), que significa ‘medida’. Fue utilizada en Francia con el nombre de mètre para designar al patrón de medida de longitud.
| Base de la definición | Fecha | Incertidumbre absoluta |
Incertidumbre relativa |
|---|---|---|---|
| 1/10 000 000 parte de la distancia entre el polo norte y el ecuador a lo largo de la línea del meridiano que pasa por París | 1795 | 0.5-0.1 (milímetros) | 10−4 |
| Primer prototipo Metre des Archives de barra de platino estándar. | 1799 | 0.05-0.01 mm | 10−5 |
| Barra de platino-iridio en el punto de fusión del hielo (1.ª Conferencia General de Pesas y Medidas) | 1889 | 0.2-0.1 µm (micrómetros) | 10−7 |
| Barra de platino-iridio en el punto de fusión del hielo, a presión atmosférica, soportada por dos rodillos (7.ª CGPM) | 1927 | n.a. | n.a. |
| Transición atómica hiperfina; 1 650 763,73 longitudes de onda de la luz en transición con kriptón 86 (11.ª CGPM) | 1960 | 0.01-0.005 µm | 10−8 |
| Distancia recorrida por la luz en el vacío en 1/299 792 458 partes de un segundo (17.ª CGPM ) | 1983 | 0.1 nm | 10−10 |
Múltiplos y submúltiplos del metro
| Submúltiplos | Múltiplos | |||||
|---|---|---|---|---|---|---|
| Valor | Símbolo | Nombre | Valor | Símbolo | Nombre | |
| 10−1 m | dm | decímetro | 101 m | dam | decámetro | |
| 10−2 m | cm | centímetro | 102 m | hm | hectómetro | |
| 10−3 m | mm | milímetro | 103 m | km | kilómetro | |
| 10−6 m | µm | micrómetro (micra) | 106 m | Mm | megámetro | |
| 10−9 m | nm | nanómetro | 109 m | Gm | gigámetro | |
| 10−12 m | pm | picómetro | 1012 m | Tm | terámetro | |
| 10−15 m | fm | femtómetro (fermi) | 1015 m | Pm | petámetro | |
| 10−18 m | am | attómetro | 1018 m | Em | exámetro | |
| 10−21 m | zm | zeptómetro | 1021 m | Zm | zettametro | |
| 10−24 m | ym | yoctómetro | 1024 m | Ym | yottametro | |
| Los prefijos más comunes aparecen en negrita. | ||||||
Equivalencias del metro
- 1 metro equivale a:
|
Véase también
En inglés: Metre Facts for Kids
