Último teorema de Fermat para niños
El Último Teorema de Fermat, también conocido como el Teorema de Fermat-Wiles, es uno de los problemas más famosos en la historia de las matemáticas. Fue propuesto por el matemático francés Pierre de Fermat en 1637. Durante más de 350 años, muchos matemáticos intentaron resolverlo sin éxito, hasta que finalmente fue demostrado en 1995 por Andrew Wiles, con la ayuda de Richard Taylor.
Este teorema dice lo siguiente:
Si tienes un número entero n que es mayor que 2, entonces no puedes encontrar tres números enteros positivos diferentes, x, y y z, que cumplan la siguiente ecuación:
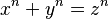
Esto significa que, por ejemplo, no hay números enteros positivos que cumplan x³ + y³ = z³, ni x⁴ + y⁴ = z⁴, y así sucesivamente para cualquier potencia mayor que 2.
La búsqueda de una solución para este teorema impulsó mucho el desarrollo de una parte de las matemáticas llamada teoría algebraica de números en los siglos XIX y XX.
Contenido
¿Qué es el Último Teorema de Fermat?
El Último Teorema de Fermat es una afirmación matemática que se mantuvo sin probar durante mucho tiempo. Fermat lo escribió por primera vez alrededor de 1637 en el margen de su copia del libro Arithmetica. En esa nota, afirmó que tenía una demostración, pero que el margen era demasiado pequeño para escribirla.
Aunque Fermat hizo otras afirmaciones que luego fueron demostradas por otros matemáticos, esta en particular fue muy difícil de probar. Por eso, durante mucho tiempo se le llamó "conjetura" (una idea que parece cierta pero no ha sido probada) en lugar de "teorema" (una afirmación que ya ha sido demostrada).
Después de 358 años de intentos por parte de muchos matemáticos, la primera demostración exitosa fue presentada en 1994 por Andrew Wiles y publicada oficialmente en 1995. Su trabajo fue considerado un "avance asombroso" en las matemáticas.
La Larga Búsqueda de la Solución
El Último Teorema de Fermat se convirtió en uno de los problemas sin resolver más importantes de las matemáticas. Antes de que se demostrara, incluso apareció en el Libro Guinness de los Récords como el "problema matemático más difícil". Esto se debía en parte a que tuvo el mayor número de intentos de demostración fallidos.
Los intentos por resolverlo llevaron a un gran avance en la teoría de números, una rama de las matemáticas que estudia las propiedades de los números enteros.
Los Orígenes: El Teorema de Pitágoras
Para entender el Último Teorema de Fermat, es útil recordar el teorema de Pitágoras. Este teorema, que seguramente conoces, dice que en un triángulo rectángulo, la suma de los cuadrados de los dos lados más cortos (catetos) es igual al cuadrado del lado más largo (hipotenusa). Se escribe como: x² + y² = z².
Existen infinitas soluciones de números enteros positivos para esta ecuación, como (3, 4, 5) o (5, 12, 13). A estas soluciones se les llama ternas pitagóricas.
Lo que Fermat propuso es que si elevas los números a una potencia mayor que 2 (por ejemplo, al cubo, a la cuarta, etc.), ya no encontrarás soluciones con números enteros positivos. Es decir, para n mayor que 2, la ecuación xn + yn = zn no tiene soluciones en números enteros positivos.
Historia de la Demostración del Teorema
Pierre de Fermat y el caso n=4
El propio Fermat fue el primero en hacer un progreso en su teorema. Él demostró que no hay soluciones para el caso cuando n = 4. Utilizó una técnica llamada "descenso infinito", que es una forma de demostración matemática.
Leonhard Euler y el caso n=3
Mucho tiempo después, en 1753, el famoso matemático Leonhard Euler afirmó haber demostrado el caso cuando n = 3. Aunque su demostración inicial tenía un pequeño error, otros trabajos suyos permitieron encontrar una solución correcta.
Sophie Germain y los casos especiales
Un gran avance fue hecho por la matemática Sophie Germain a principios del siglo XIX. Ella encontró una forma de probar el teorema para una clase entera de números primos. Su trabajo ayudó a dividir el problema en dos casos, lo que simplificó la búsqueda de la solución.
Ernst Kummer y los primos regulares
A mediados del siglo XIX, Ernst Kummer amplió el trabajo de Sophie Germain. Demostró el teorema para un tipo de números primos llamados "primos regulares". Sin embargo, quedaban los "primos irregulares", que eran más difíciles de manejar. A pesar de los esfuerzos, una demostración para todos los números parecía inalcanzable en ese momento.
| Año | Acontecimiento |
|---|---|
| 1665 | Muere Fermat sin dejar la demostración. |
| 1753 | Leonhard Euler demuestra el caso n = 3. |
| 1825 | Adrien-Marie Legendre demuestra el caso para n = 5. |
| 1839 | Gabriel Lamé demuestra el caso n = 7. |
| 1843 | Ernst Kummer hace un gran avance, pero se encuentra un error. |
| 1995 | Andrew Wiles publica la demostración completa del teorema. |
Andrew Wiles y la Solución Final
La solución definitiva llegó en 1995 de la mano del matemático británico Andrew Wiles. Wiles había estado fascinado por el Último Teorema de Fermat desde su infancia. Trabajó en secreto durante seis años en el problema.
Su gran logro fue demostrar una parte importante de otra conjetura matemática, conocida como el teorema de la modularidad (antes llamada conjetura de Taniyama-Shimura). Esta conjetura conecta dos áreas de las matemáticas que parecían muy diferentes: las curvas elípticas y las formas modulares.
En 1984, el matemático Gerhard Frey notó una posible conexión entre el Último Teorema de Fermat y la conjetura de Taniyama-Shimura. Más tarde, Ken Ribet demostró que si la conjetura de Taniyama-Shimura era cierta, entonces el Último Teorema de Fermat también lo sería. Esto significaba que si alguien podía demostrar la conjetura de Taniyama-Shimura, ¡automáticamente resolvería el Último Teorema de Fermat!
Aunque ambas conjeturas eran consideradas extremadamente difíciles de probar, Wiles decidió intentar demostrar la conjetura de Taniyama-Shimura. En 1993, anunció su demostración. Durante la revisión de su trabajo, se encontró un pequeño error, pero Wiles, con la ayuda de su antiguo alumno Richard Taylor, logró corregirlo en un año.
La demostración final de Wiles, publicada en 1995, fue un trabajo enorme y complejo. Su logro fue muy celebrado en todo el mundo y se hizo popular a través de libros y programas de televisión. Por su trabajo, Andrew Wiles recibió muchos premios, incluyendo el prestigioso Premio Abel en 2016.
El trabajo de Wiles no solo resolvió el Último Teorema de Fermat, sino que también abrió nuevas e importantes áreas de investigación en las matemáticas modernas.
Véase también
 En inglés: Fermat's Last Theorem Facts for Kids
En inglés: Fermat's Last Theorem Facts for Kids
- Pierre de Fermat
- Pequeño teorema de Fermat
- Número primo de Fermat
- Espiral de Fermat
- Conjetura de Beal


