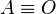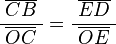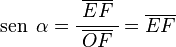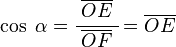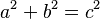Trigonometría para niños
La trigonometría es una parte de las matemáticas que estudia las relaciones entre los lados y los ángulos de los triángulos. Su nombre viene de palabras griegas que significan "medición de triángulos".
En general, la trigonometría se enfoca en las "razones trigonométricas". Estas son el seno, coseno, tangente, cotangente, secante y cosecante. La trigonometría se usa en otras áreas de la geometría, como la geometría plana o la geometría del espacio. También es útil en ecuaciones diferenciales y series de Fourier.
Tiene muchas aplicaciones prácticas. Por ejemplo, las técnicas de triangulación se usan en astronomía para medir distancias a estrellas cercanas. También se usa para medir distancias entre lugares en la Tierra y en los sistemas de navegación por satélite (como el GPS).

Datos para niños Trigonometría |
||
|---|---|---|
 |
||
| Referencias | ||
| Constantes exactas ·Tablas ·Circunferencia goniométrica |
||
| Funciones, leyes y teoremas | ||
| Funciones e (inversas) ·Senos ·Cosenos ·Tangentes ·Cotangentes ·Teorema de Pitágoras·Identidades y fórmulas de trigonometría |
||
| Cálculo infinitesimal | ||
| Sustitución trigonométrica ·Integrales de funciones directas (e inversas) ·Derivadas | ||
| Temas relacionados | ||
| Temas ·Historia ·Usos·Trigonometría generalizada |
Contenido
- Historia de la trigonometría
- Cómo se miden los ángulos
- Las funciones trigonométricas
- Equivalencia entre las funciones trigonométricas
- Valores de las funciones trigonométricas
- Cómo se comportan las funciones trigonométricas
- Cálculo de algunos casos especiales
- Identidades trigonométricas
- Seno y coseno en números complejos
- Más información
- Véase también
Historia de la trigonometría

Los antiguos egipcios y babilonios ya conocían cómo se relacionaban los lados de los triángulos que eran similares. Sin embargo, no tenían una forma de medir los ángulos como la conocemos hoy. Por eso, estudiaban los lados de los triángulos por su longitud.
Los astrónomos babilonios registraban cuándo salían y se ponían las estrellas. También seguían el movimiento de los planetas y los eclipses. Todo esto necesitaba saber la distancia angular en el cielo. Algunos expertos creen que una tablilla babilonia llamada Plimpton 322 (de hace unos 3900 años) podría ser una tabla de trigonometría. Sin embargo, hay un debate sobre si es una tabla de triángulos especiales o de otro tipo de cálculos.

Los egipcios, hace más de 3000 años, usaban una forma sencilla de trigonometría para construir las pirámides. El Papiro de Ahmes, escrito por Ahmes (hace unos 3600 años), tiene un problema que usa trigonometría:
- Si una pirámide mide 250 codos de alto y el lado de su base es de 360 codos, ¿cuál es su Seked?
La solución a este problema es la relación entre la mitad del lado de la base y la altura de la pirámide. Esto es como calcular la cotangente del ángulo que forma la base con la cara de la pirámide.
Cómo se miden los ángulos
Para medir ángulos en trigonometría, usamos tres unidades principales. La más común en la vida diaria es el grado sexagesimal. Sin embargo, en matemáticas, el radián es la unidad más usada. El grado centesimal se usa en áreas como la topografía y la construcción.
- Radián: Es la unidad natural para medir ángulos en matemáticas. Una vuelta completa a un círculo tiene 2π radianes (aproximadamente 6.28 radianes).
- Grado sexagesimal: Divide un círculo completo en 360 grados.
- Grado centesimal: Divide un círculo en 400 grados centesimales.
- Mil angular: Divide un círculo en 6400 unidades.
 |
 |
| Transportador en radianes | Transportador en grados sexagesimales |
 |
 |
| Transportador en grados centesimales | Transportador en mil angular |
Las funciones trigonométricas
La trigonometría es una parte importante de las matemáticas. Estudia la relación entre los lados y los ángulos de un triángulo rectángulo y una circunferencia. Para esto, se crearon varias funciones. Estas funciones se han vuelto muy importantes y se usan en muchos campos.
Razones trigonométricas básicas
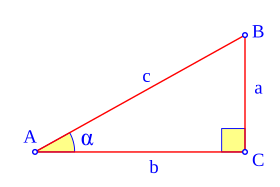
Imagina un triángulo ABC que tiene un ángulo recto en C. Si el lado más largo (la hipotenusa, AB) mide 1, podemos definir las razones seno, coseno y tangente para el ángulo 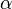 en el vértice A.
en el vértice A.
- El seno (abreviado sen o sin) es la relación entre el lado opuesto al ángulo y la hipotenusa.
- El coseno (abreviado cos) es la relación entre el lado junto al ángulo (adyacente) y la hipotenusa.
- La tangente (abreviado tan o tg) es la relación entre el lado opuesto al ángulo y el lado adyacente.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg}\alpha = \frac{\overline{CB}}{\overline{AC}} = \frac{\overline{DE}}{\overline{AD}} = \frac{\overline{DE}}{1} = \overline{DE}
Cómo se ven en una gráfica
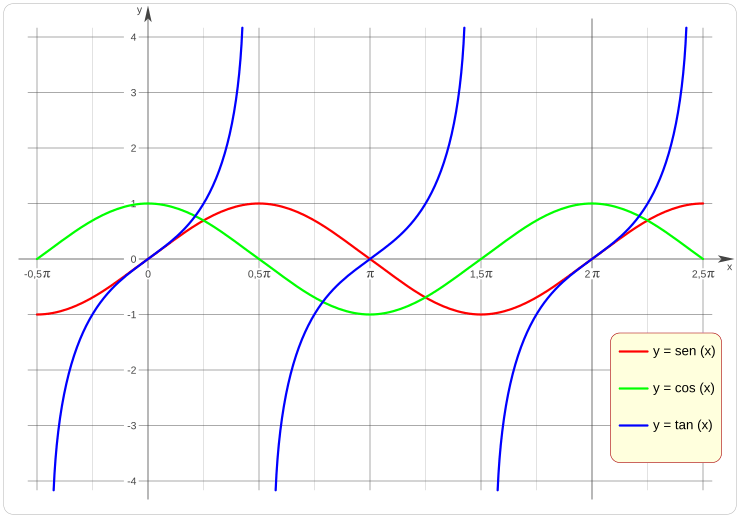
Razones trigonométricas inversas
- La cosecante: (abreviado csc o cosec) es la inversa del seno.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc \alpha = \frac{1}{\sen \; \alpha} = \frac{\overline{AB}}{\overline{CB}} = \frac{\overline{AG}}{\overline{AF}} = \frac{\overline{AG}}{1} = \overline{AG}
- La secante: (abreviado sec) es la inversa del coseno.
- La cotangente: (abreviado cot o ctg) es la inversa de la tangente.
Generalmente, se usan más el seno, coseno y tangente. Las otras (cosecante, secante y cotangente) se usan menos, a menos que sea necesario para simplificar cálculos.
Cómo se ven en una gráfica
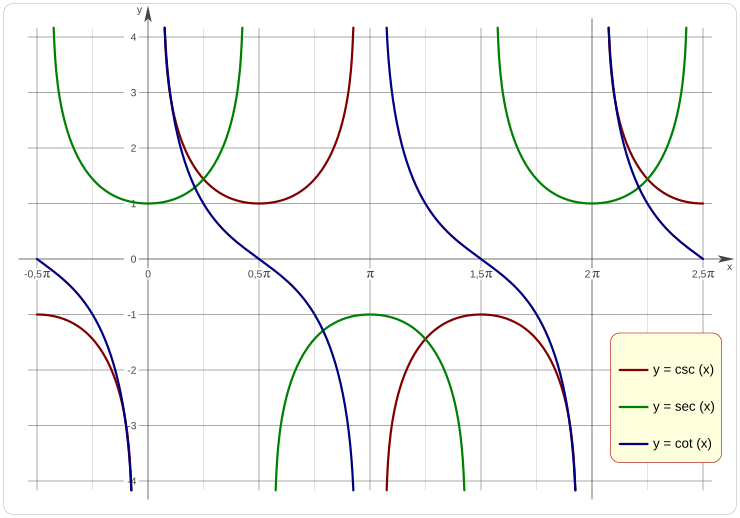
Otras funciones trigonométricas
Existen otras funciones trigonométricas que se pueden definir usando las que ya vimos. No son tan comunes, pero tienen un significado geométrico.
- El seno cardinal o función sinc (x):
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname{sinc} \; (x) = \frac{\sen(x)}{x}
- El verseno: Es la distancia entre la cuerda y el arco en una circunferencia.
- El semiverseno: Se usa en navegación.
- El coverseno:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {coversin} \; \alpha = 1 - \sen \; \alpha
- El semicoverseno:
- La exsecante:
Funciones trigonométricas recíprocas (arco)
Cuando un ángulo se mide en radianes, a menudo se le llama "arco". Por eso, las funciones inversas de las trigonométricas se llaman con el prefijo "arco". Cada razón trigonométrica tiene su función inversa:
Si y es igual al seno de x:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y= \sen \, x \,
La función inversa es:
Esto significa que x es el arco cuyo seno es y, o x es el arcoseno de y.
Si y es igual al coseno de x:
La función inversa es:
Esto significa que x es el arco cuyo coseno es y, o x es el arcocoseno de y.
Si y es igual a la tangente de x:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y= \operatorname {tg} x \,
La función inversa es:
Esto significa que x es el arco cuya tangente es y, o x es el arcotangente de y.
¡Importante! A veces, las funciones inversas se escriben así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = \operatorname {arcsin} \; x \quad \longrightarrow \quad y = \sen^{-1} x \,
Pero ten cuidado de no confundirlas con:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): y = \cfrac{1}{\sen x} \quad \longrightarrow \quad y = \csc x
Esta última es la cosecante, que es la inversa multiplicativa, no la función inversa.
Cómo se ven en una gráfica
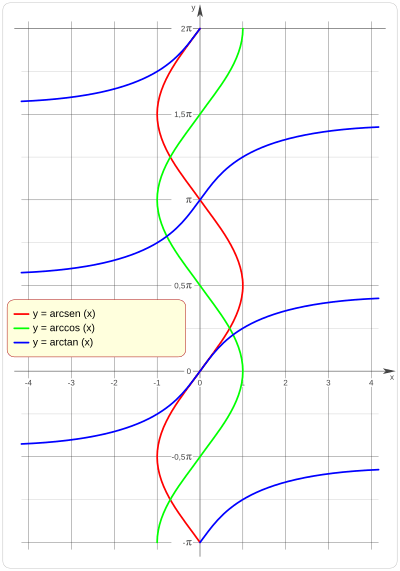
Si dibujamos estas funciones inversas tal cual, verás que para un valor de 'x', puede haber muchos valores de 'y'. Esto no cumple con la definición de una función, que dice que para cada 'x' solo debe haber un 'y'. Por ejemplo, el arcoseno de 0 es 0, pero también puede ser cualquier múltiplo de  .
.
Para cualquier número entero n.
Para que estas funciones inversas cumplan con la definición de función (que cada 'x' tenga solo un 'y'), se limita el rango de valores que pueden tomar. Así, se asegura que funcionen correctamente.
La función arcoseno se define:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rccl} \arcsin : & [-1,1] & \to & [-0,5 \pi \; , \; 0,5 \pi] \\ & x & \mapsto & y = \arcsin(x) \end{array}
La función arcocoseno se define:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rccl} \arccos : & [-1,1] & \to & [0 \; , \; \pi] \\ & x & \mapsto & y = \arccos(x) \end{array}
La función arcotangente se define:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rccl} \arctan : & R & \to & [-0,5 \pi \; , \; 0,5 \pi] \\ & x & \mapsto & y = \arctan(x) \end{array}
Funciones trigonométricas inversas recíprocas
De manera similar, las funciones inversas de la cosecante, secante y cotangente también usan el prefijo "arco".
Si y es igual a la cosecante de x:
La función inversa es:
Esto significa que x es el arco cuya cosecante es y, o x es la arcocosecante de y.
Si y es igual a la secante de x:
La función inversa es:
Esto significa que x es el arco cuya secante es y, o x es el arcosecante de y.
Si y es igual a la cotangente de x:
La función inversa es:
Esto significa que x es el arco cuya cotangente es y, o x es el arcocotangente de y.
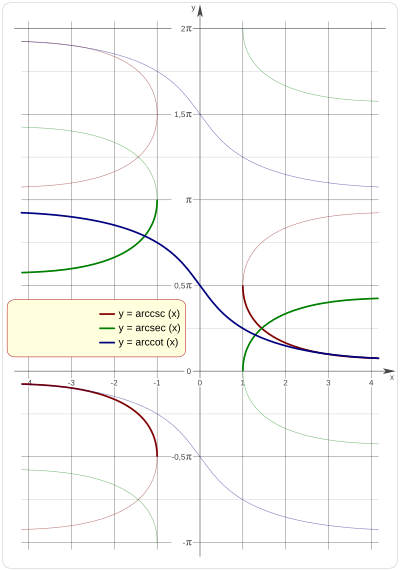
Cómo se ven en una gráfica
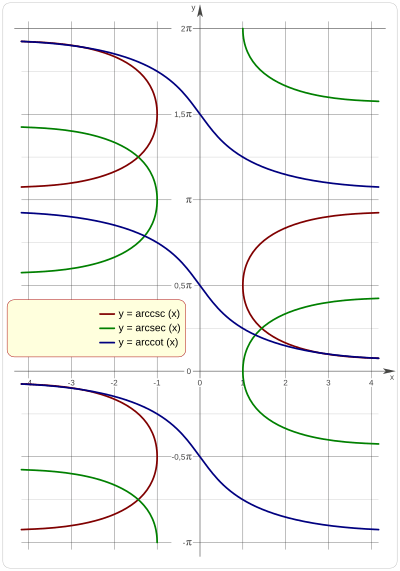
Al igual que con las funciones inversas básicas, si las dibujamos sin restricciones, no cumplen con la definición de función.
Para que cumplan con la definición de función, también se limitan sus dominios y codominios.
La función arcocosecante se define:
La función arcosecante se define:
La función arcocotangente se define:
Estas restricciones aseguran que las funciones sean válidas.
Equivalencia entre las funciones trigonométricas
Las funciones trigonométricas están relacionadas entre sí. Aquí puedes ver cómo se pueden expresar unas en términos de otras:
| Seno | Coseno | Tangente | Cotangente | Secante | Cosecante | |
|---|---|---|---|---|---|---|
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen\theta\, |
|
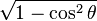 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\operatorname {tg}\theta}{\sqrt{1+\operatorname {tg}^{2}\theta}} | 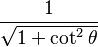 |
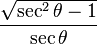 |
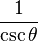 |
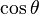 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{1-\sen^{2}\theta} |
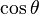 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{\sqrt{1+\operatorname {tg}^{2}\theta}} | 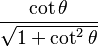 |
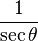 |
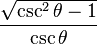 |
| Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg}\theta\, | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sen\theta}{\sqrt{1-\sen^{2}\theta}} | 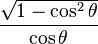 |
|
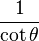 |
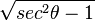 |
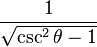 |
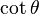 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sqrt{1-\sen^{2}\theta}}{\sen\theta} | 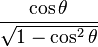 |
|
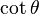 |
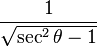 |
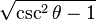 |
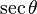 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{1}{\sqrt{1-\sen^{2}\theta}} |
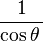 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sqrt{1+\operatorname {tg}^{2}\theta} | 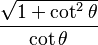 |
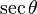 |
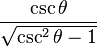 |
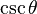 |
|
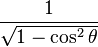 |
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sqrt{1+\operatorname {tg}^{2}\theta}}{\operatorname {tg}\theta} | 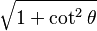 |
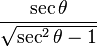 |
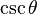 |
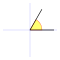
Valores de las funciones trigonométricas
Aquí tienes algunos valores importantes de las funciones trigonométricas que es bueno recordar:
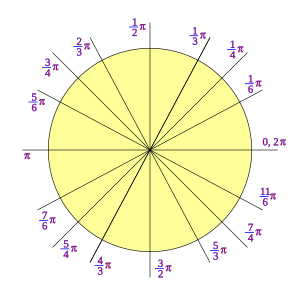 |
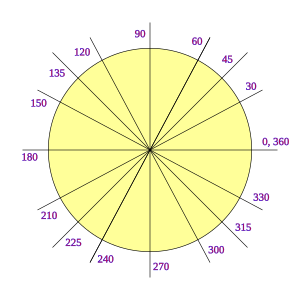 |
| Circunferencia en radianes. | Circunferencia en grados sexagesimales. |
| Radianes | Grados sexagesimales |
seno | coseno | tangente | cosecante | secante | cotangente | |
|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
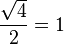 |
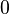 |
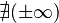 |
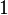 |
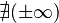 |
 |
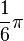 |
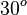 |
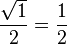 |
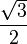 |
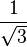 |
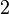 |
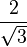 |
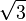 |
 |
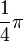 |
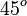 |
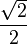 |
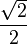 |
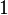 |
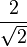 |
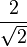 |
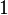 |
 |
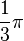 |
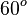 |
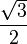 |
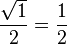 |
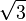 |
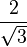 |
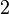 |
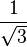 |
 |
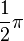 |
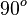 |
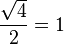 |
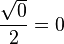 |
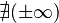 |
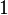 |
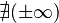 |
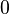 |
Antiguamente, para calcular estos valores, se usaban tablas trigonométricas. La primera fue creada por Johann Müller Regiomontano en 1467. Hoy en día, las calculadoras y los programas de computadora hacen estos cálculos al instante, así que las tablas ya no se usan.
Cómo se comportan las funciones trigonométricas
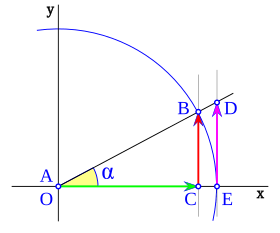
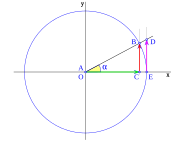
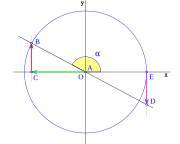
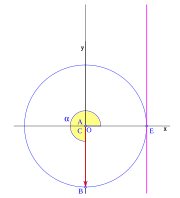
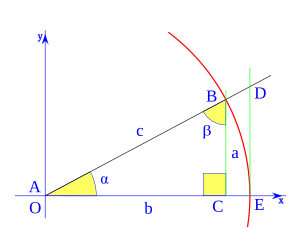
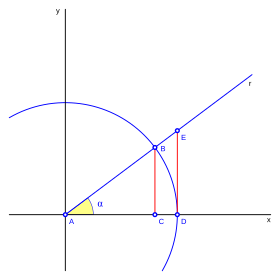
Imagina un plano con ejes x e y que se cruzan en el punto O. Dibuja un círculo con centro en O y radio 1 (llamado circunferencia goniométrica). El punto donde el círculo corta el eje x positivo es E.
El punto A es el vértice del triángulo, y O es el centro del sistema.
Una línea r pasa por O y forma un ángulo 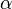 con el eje x. Esta línea corta el círculo en el punto B. Una línea vertical desde B corta el eje x en C. Otra línea vertical desde E corta la línea r en el punto D.
con el eje x. Esta línea corta el círculo en el punto B. Una línea vertical desde B corta el eje x en C. Otra línea vertical desde E corta la línea r en el punto D.
Por la semejanza de triángulos, podemos ver que:
Como los puntos E y B están en el círculo de radio 1, las distancias 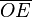 y
y 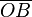 son 1. Usando las definiciones de las funciones trigonométricas:
son 1. Usando las definiciones de las funciones trigonométricas:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen \alpha =& \!\!\! \overline{CB} \\ \cos \alpha =& \!\!\! \overline{OC} \\ \operatorname {tg} \alpha =& \!\!\! \overline{ED} \end{array}
Entonces, tenemos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \frac{\sen \alpha}{ \cos \alpha} = \frac{\operatorname {tg} \alpha}{1}
Esto nos muestra que la tangente es la división del seno entre el coseno.
Primer cuadrante
Para entender cómo cambian las funciones trigonométricas, vamos a recorrer el círculo completo, cuadrante por cuadrante. Empezamos en el primer cuadrante, con un ángulo de cero.
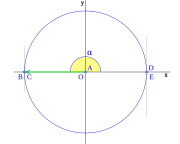
Cuando el ángulo 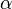 es 0, los puntos B, D y C están en E. Por lo tanto:
es 0, los puntos B, D y C están en E. Por lo tanto:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen 0 =& \!\!\! 0 \\ \cos 0 =& \!\!\! 1 \\ \operatorname {tg} 0 =& \!\!\! 0 \end{array}
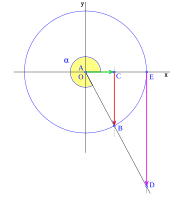
Si aumentamos el ángulo 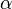 , las distancias
, las distancias 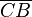 (seno) y
(seno) y 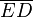 (tangente) aumentan. Mientras tanto,
(tangente) aumentan. Mientras tanto, 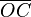 (coseno) disminuye.
(coseno) disminuye.
Recuerda que el punto B se mueve sobre el círculo a medida que el ángulo cambia. El punto E (donde el círculo corta el eje x) no se mueve.
Los segmentos 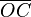 y
y 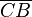 están dentro del círculo, así que su valor máximo es 1. Pero
están dentro del círculo, así que su valor máximo es 1. Pero 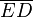 (la tangente) no está limitado. Cuando el ángulo
(la tangente) no está limitado. Cuando el ángulo 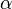 llega a 90 grados (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,5 \pi \, rad), la línea r es vertical. Como dos líneas verticales no se cruzan, la distancia
llega a 90 grados (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 0,5 \pi \, rad), la línea r es vertical. Como dos líneas verticales no se cruzan, la distancia 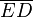 se vuelve infinita.
se vuelve infinita.
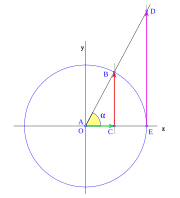
En 90 grados, el punto C coincide con A, y el coseno es cero. El punto B está en el punto más alto del eje y, y el seno es uno.
Para un ángulo recto (90 grados), las funciones tienen estos valores:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen ({\pi}/{2}) =& \!\!\! 1 \\ \cos ({\pi}/{2}) =& \!\!\! 0 \\ \operatorname {tg} ({\pi}/{2}) =& \!\!\! \pm\infty \to \mathrm{No \; definida} \end{array}
Segundo cuadrante
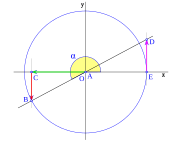
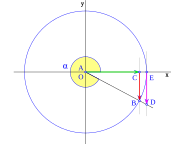
Cuando el ángulo 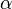 pasa de 90 grados, el seno (segmento
pasa de 90 grados, el seno (segmento 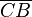 ) empieza a disminuir. El coseno (segmento
) empieza a disminuir. El coseno (segmento 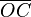 ) aumenta, pero en la dirección negativa del eje x. Esto significa que el coseno se vuelve negativo.
) aumenta, pero en la dirección negativa del eje x. Esto significa que el coseno se vuelve negativo.
La tangente, que era infinita en 90 grados, se vuelve negativa en el segundo cuadrante. Su valor absoluto disminuye a medida que el ángulo 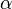 se acerca a 180 grados (
se acerca a 180 grados (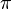 rad).
rad).
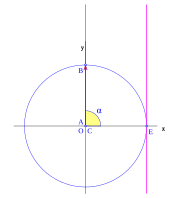
En resumen: en el segundo cuadrante, el seno de 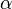 disminuye de 1 (a 90 grados) a 0 (a 180 grados). El coseno se vuelve negativo y cambia de 0 (a 90 grados) a -1 (a 180 grados).
disminuye de 1 (a 90 grados) a 0 (a 180 grados). El coseno se vuelve negativo y cambia de 0 (a 90 grados) a -1 (a 180 grados).
La tangente sigue siendo la división del seno entre el coseno, manteniendo los signos.
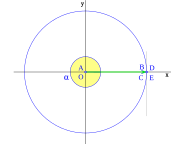
Para un ángulo llano (180 grados), el punto D está en E, y B y C están en el eje x en el lado opuesto a E. Así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen \; \pi =& \!\!\! 0 \\ \cos \pi =& \!\!\! -1 \\ \operatorname {tg} \pi =& \!\!\! 0 \end{array}
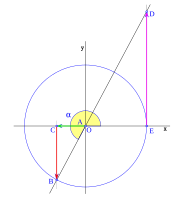
Tercer cuadrante
En el tercer cuadrante, que va de 180 grados (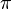 rad) a 270 grados (
rad) a 270 grados (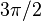 rad), los valores del seno, coseno y tangente cambian.
rad), los valores del seno, coseno y tangente cambian.
Para 270 grados:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen ({3\pi}/{2}) =& \!\!\! -1 \\ \cos ({3\pi}/{2}) =& \!\!\! 0 \\ \operatorname {tg} ({3\pi}/{2}) =& \!\!\! \infty \to \text{No definida} \end{array}
A medida que el ángulo 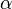 aumenta, el seno se vuelve más negativo (su valor absoluto aumenta). El coseno se vuelve más pequeño en valor absoluto, pero sigue siendo negativo. La tangente aumenta, igual que en el primer cuadrante.
aumenta, el seno se vuelve más negativo (su valor absoluto aumenta). El coseno se vuelve más pequeño en valor absoluto, pero sigue siendo negativo. La tangente aumenta, igual que en el primer cuadrante.
El seno, coseno y tangente mantienen la misma relación:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg} \alpha = \frac{\sen \alpha} {\cos \alpha}
Esto se cumple tanto en valor como en signo. Cuando el coseno se acerca a cero, la tangente tiende a infinito.
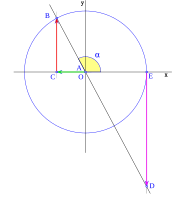
Cuarto cuadrante
En el cuarto cuadrante, que va de 270 grados (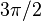 rad) a 360 grados (
rad) a 360 grados (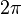 rad), las funciones trigonométricas cambian desde sus valores en 270 grados:
rad), las funciones trigonométricas cambian desde sus valores en 270 grados:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen (3\pi/2 ) =& \!\!\! -1 \\ \cos(3\pi/2 ) =& \!\!\! 0 \\ \operatorname {tg}(3\pi/2 ) =& \!\!\! \infty \to \text{No definida} \end{array}
Hasta los valores que toman al completar una vuelta (360 grados o 0 grados):
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rlcl} \sen (2 \, \pi ) =& \!\! \sen 0 & \!\!\!=& \!\!0 \\ \cos(2 \, \pi ) =& \!\! \cos 0 &\!\!\!=& \!\!1 \\ \operatorname {tg}(2 \, \pi ) =& \!\! \operatorname {tg} 0 &\!\!\!=& \!\!0 \end{array}
A medida que el ángulo 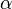 aumenta, el coseno (
aumenta, el coseno (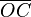 ) aumenta en el lado positivo del eje x. El seno (
) aumenta en el lado positivo del eje x. El seno (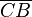 ) disminuye en el lado negativo del eje y. La tangente (
) disminuye en el lado negativo del eje y. La tangente (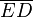 ) también disminuye en el lado negativo del eje y.
) también disminuye en el lado negativo del eje y.
Cuando 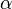 llega a 360 grados (o 0 grados), los puntos B, C y D vuelven a coincidir en E. Esto hace que el seno y la tangente sean cero, y el coseno sea uno, igual que al principio del primer cuadrante.
llega a 360 grados (o 0 grados), los puntos B, C y D vuelven a coincidir en E. Esto hace que el seno y la tangente sean cero, y el coseno sea uno, igual que al principio del primer cuadrante.
Debido a que las funciones trigonométricas son cíclicas, siempre se cumple que:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen \; \alpha =& \!\!\! \sen(\alpha + 2 \, \pi \, n ) \\ \cos \alpha =& \!\!\! \cos (\alpha + 2 \, \pi \, n ) \\ \operatorname {tg} \alpha =& \!\!\! \operatorname {tg}(\alpha + 2 \, \pi \, n ) \end{array}
Esto significa que cualquier función trigonométrica tendrá el mismo valor si le sumas o restas un número entero de vueltas completas al ángulo.
Cálculo de algunos casos especiales
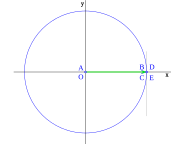
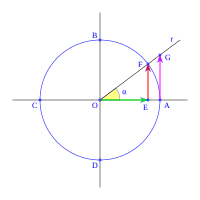
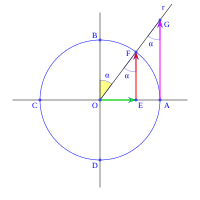
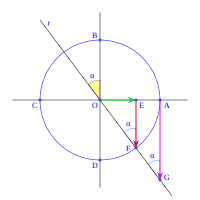
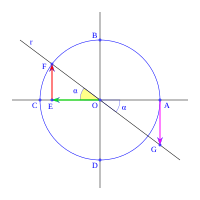
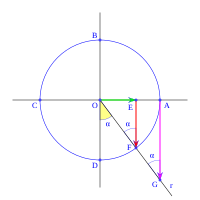
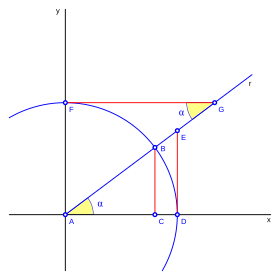
Imagina un círculo de radio uno, dividido en cuatro partes por dos líneas perpendiculares que se cruzan en el centro O. Estas líneas cortan el círculo en los puntos A, B, C y D. La línea horizontal AC es el eje x, y la vertical BD es el eje y.
Ahora, dibuja una línea r que pasa por el centro O y forma un ángulo α con el eje OA (eje x). Esta línea corta el círculo en F. Una línea vertical desde F corta el eje x en E. Una línea vertical desde A corta la línea r en G.
Con esto, definimos las funciones trigonométricas como vimos antes:
Para el seno:
Porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{OF} = 1 (es el radio del círculo unitario).
Para el coseno:
Porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{OF} = 1 .
Para la tangente:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg} \; \alpha = \cfrac{\; \overline{EF} \;}{\overline{OE}} = \cfrac{\; \overline{AG} \;}{\overline{OA}} = \overline{AG}
Porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \overline{OA} = 1 .
Usando estas definiciones, podemos entender algunos casos importantes:
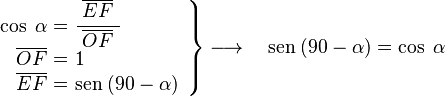
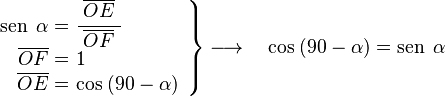
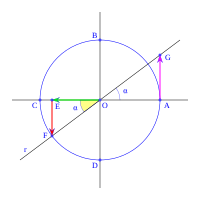
Para 90-α
Si medimos un ángulo α en sentido horario desde el eje vertical OB, la línea r forma un ángulo 90-α con el eje x. Podemos encontrar las funciones trigonométricas de este ángulo si conocemos las de α.
En el triángulo OEF, que tiene un ángulo recto en E y el ángulo en F es α:
En el mismo triángulo OEF:
En el triángulo OAG, que tiene un ángulo recto en A y el ángulo en G es α:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! \operatorname {tg} \; (90-\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (90-\alpha) = \cfrac{1}{\operatorname {tg} \; \alpha}
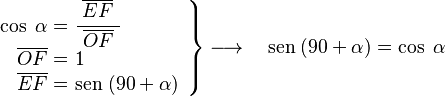
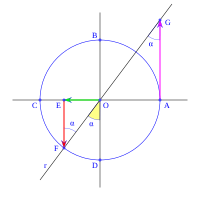
Para 90+α
Si desde el eje vertical OB trazamos la línea r con un ángulo α (en sentido antihorario), el ángulo entre el eje horizontal OA y la línea r será 90+α. La línea r extendida corta el círculo en F y la línea vertical que pasa por A en G.
El triángulo OEF es un triángulo rectángulo en E, y su ángulo en F es α. Por lo tanto:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A y tiene el ángulo α en G:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! -\operatorname {tg} \; (90+\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (90+\alpha) = \cfrac{-1}{\operatorname {tg} \; \alpha}
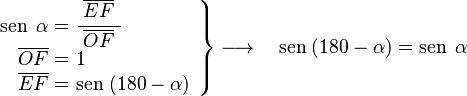
Para 180-α
Si desde el eje horizontal OC trazamos la línea r con un ángulo α, el ángulo entre el eje OA y la línea r es de 180-α. En el triángulo OEF, que es rectángulo en E y tiene el ángulo α en O:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A y tiene el ángulo α en O:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! -\operatorname {tg} \; (180-\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (180-\alpha) = -\operatorname {tg} \; \alpha
Para 180+α
En el círculo de radio uno, si trazamos la línea r con un ángulo α desde el eje OC, el ángulo entre el eje OA y la línea r es de 180+α. En el triángulo OEF, que es rectángulo en E:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! \operatorname {tg} \; (180+\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (180+\alpha) = \operatorname {tg} \; \alpha
Para 270-α
Desde el eje OD y con un ángulo α medido en sentido horario, trazamos la línea r. El ángulo entre el eje OA y la línea r es de 270-α. En el triángulo OEF, que es rectángulo en E:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A y tiene el ángulo α en G:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! \operatorname {tg} \; (270-\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (270-\alpha) = \cfrac{1}{\operatorname {tg} \; \alpha}
Para 270+α
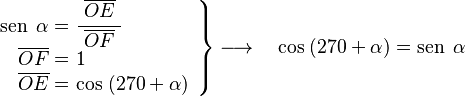
Desde el eje OD y con un ángulo α medido en sentido antihorario, trazamos la línea r. El ángulo entre el eje OA y la línea r es de 270+α. En el triángulo OEF, que es rectángulo en E:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A y tiene el ángulo α en G:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{OA} \;}{\overline{AG}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! -\operatorname {tg} \; (270+\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (270+\alpha) = \cfrac{-1}{\operatorname {tg} \; \alpha}
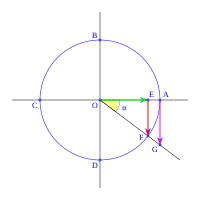
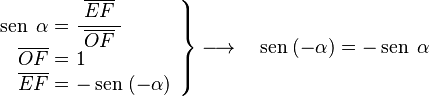
Para -α
En el círculo de radio uno, si trazamos la línea r con un ángulo α medido en sentido horario desde el eje OA, el ángulo entre el eje OA y la línea r es de -α (o 360-α). En el triángulo OEF, que es rectángulo en E:
En el mismo triángulo OEF:
En el triángulo OAG, que es rectángulo en A:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \left . \begin{array}{rl} \operatorname {tg} \; \alpha =& \!\!\! \cfrac{\; \overline{AG} \;}{\overline{OA}} \\ \overline{OA} =& \!\!\! 1 \\ \overline{AG} =& \!\!\! -\operatorname {tg} \; (-\alpha) \end{array} \right \} \longrightarrow \quad \operatorname {tg} \; (-\alpha) = -\operatorname {tg} \; \alpha
Identidades trigonométricas
Una identidad es una igualdad que se cumple para todos los valores posibles de una variable. En trigonometría, hay seis identidades fundamentales:
Identidades recíprocas
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \begin{array}{rl} \sen (\alpha) \cdot \csc (\alpha) =& \!\!\! 1 \\ \cos (\alpha) \cdot \sec (\alpha) =& \!\!\! 1 \\ \operatorname {tg} (\alpha) \cdot \cot (\alpha) =& \!\!\! 1 \end{array}
Identidades de división
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg} (\alpha) = \frac {\sen (\alpha)}{ \cos (\alpha)}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cot (\alpha) = \frac {\cos (\alpha)}{ \sen (\alpha)}
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc (\alpha) = \frac { 1 }{ \sen (\alpha)}
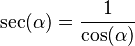
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \cot (\alpha) = \frac { 1 }{ \operatorname {tg} (\alpha)}
Identidades basadas en el teorema de Pitágoras
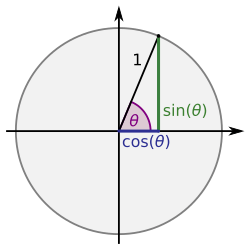
En un triángulo rectángulo, se cumple el Teorema de Pitágoras:
Donde 'a' y 'b' son los catetos, y 'c' es la hipotenusa.
De la figura anterior, sabemos que:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen (\alpha ) = \frac {a}{c}, \qquad \cos (\alpha ) = \frac {b}{c}
Si elevamos al cuadrado el seno y el coseno y los sumamos:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen^2 \alpha + \cos^2 \alpha = \bigg(\dfrac {a}{c}\bigg) ^2 + \bigg(\frac {b}{c}\bigg)^2 = \frac {a^2 + b^2 }{c^2} = \frac {c^2}{c^2} = 1
Así, para cualquier ángulo α, se cumple la identidad Pitagórica:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen^2 \alpha + \cos^2 \alpha = 1 \,
También se pueden expresar de estas otras formas:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg}^2 \alpha + 1 = \sec^2 \alpha \,
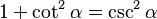
Seno y coseno en números complejos
El seno y el coseno también se pueden definir usando números complejos, gracias a la fórmula de Euler:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen \alpha= \dfrac {e^{i\alpha}-e^{-i\alpha}}{2i}, \qquad \cos \alpha= \frac {e^{i\alpha}+e^{-i\alpha}}{2}
Donde 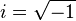 .
.
Por lo tanto, la tangente se define como:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \operatorname {tg} \alpha =\dfrac{1}{i} \dfrac {e^{i\alpha}-e^{-i\alpha}}{e^{i\alpha}+e^{-i\alpha}} =\ {-i} \dfrac {e^{i\alpha}-e^{-i\alpha}}{e^{i\alpha}+e^{-i\alpha}}
Más información
- Historia de la trigonometría
- Función trigonométrica
- Identidad trigonométrica
- Funciones hiperbólicas
- Hexágono trigonométrico: Una herramienta para recordar relaciones trigonométricas.
- Fórmula de Euler y Número complejo, para entender las funciones trigonométricas complejas.
- Trigonometría esférica
Véase también
 En inglés: Trigonometry Facts for Kids
En inglés: Trigonometry Facts for Kids


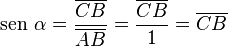
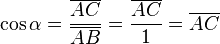
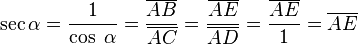
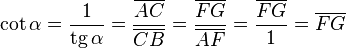

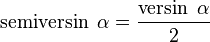
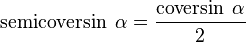

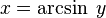
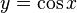
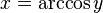
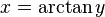
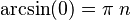
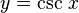
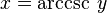
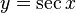
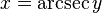
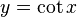
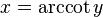
![\begin{array}{rccl}
\arccsc : & (-\infty , -1] \cup [1 , \infty) & \to & [-0,5 \pi \; , \; 0,5 \pi] \\
& x & \to & y = \arccsc(x)
\end{array}](/images/math/1/c/0/1c0cc5acbc55d2704fae990b45e423cd.png)
![\begin{array}{rccl}
\arcsec : & (-\infty , -1] \cup [1 , \infty) & \to & [0 \; , \; \pi] \\
& x & \to & y = \arcsec(x)
\end{array}](/images/math/b/8/d/b8dd135c0ae5f6ef7afaf512298a9eb8.png)
![\begin{array}{rccl}
\arccot : & R & \to & [0 \; , \; \pi] \\
& x & \to & y = \arccot(x)
\end{array}](/images/math/f/e/a/feadbaa1d0e88afe9687533becf2f2df.png)