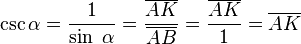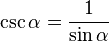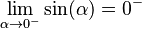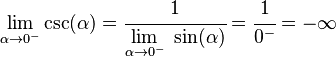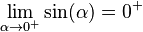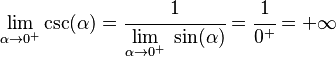Cosecante para niños
La función cosecante (abreviada como csc o cosec) es una de las funciones más importantes en la Trigonometría. Imagina que es como la "pareja inversa" de la función seno. Esto significa que si multiplicas el seno de un ángulo por su cosecante, el resultado siempre será 1.
En matemáticas, lo escribimos así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc \alpha = \frac{1}{\sin \alpha}
Aquí, 
(alfa) representa un ángulo. Si pensamos en un triángulo rectángulo, donde 'c' es la hipotenusa (el lado más largo) y 'a' es el lado opuesto al ángulo , entonces la cosecante también se puede expresar como:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc \alpha = \frac{c}{a}
Contenido
¿Qué es la Función Cosecante?
La función cosecante es el valor inverso de la función seno. Esto significa que para calcular la cosecante de un ángulo, simplemente divides 1 entre el valor del seno de ese mismo ángulo. Es una herramienta muy útil para resolver problemas relacionados con triángulos y ondas.
La Cosecante en la Geometría
Podemos entender la cosecante de un ángulo observando cómo se representa en un círculo unitario (un círculo con radio 1).
¿Cómo se ve la Cosecante en un círculo?
Si tenemos un ángulo en un círculo unitario, la función seno de ese ángulo es la longitud del lado opuesto en un triángulo rectángulo formado dentro del círculo. La cosecante, al ser su inversa, se puede visualizar de otra manera.
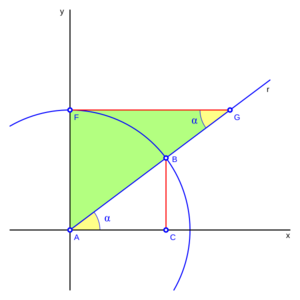
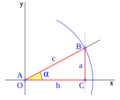
Observa la imagen. Si trazamos una línea horizontal que pasa por el punto F y corta la línea r (que es la hipotenusa de un triángulo más grande) en el punto G, podemos ver que el segmento AG representa la cosecante del ángulo . Esto es porque en el triángulo GAF, que es un triángulo rectángulo en F, el lado AF mide 1 (es el radio del círculo unitario).
La fórmula se ve así:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \csc \alpha = \frac{1}{\sin \; \alpha} = \frac{\overline{AG}}{\overline{AF}} = \frac{\overline{AG}}{1} = \overline{AG}
Otra forma de ver la Cosecante
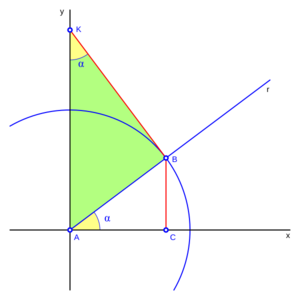
Hay otra manera de dibujar la cosecante. Si desde el punto B (donde el ángulo toca el círculo) trazamos una línea perpendicular a la línea r, y esta línea corta el eje vertical (eje 'y') en el punto K, entonces el segmento AK también representa la cosecante del ángulo .
La fórmula para esta representación es:
Ambas representaciones nos ayudan a entender visualmente qué significa la cosecante.
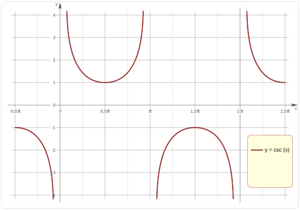
¿Cómo se dibuja la Función Cosecante?
La representación gráfica de la función cosecante es muy interesante. Se ve como una serie de curvas que se repiten.
Relación entre la Función Seno y la Cosecante
Como ya sabemos, la cosecante es el inverso del seno:
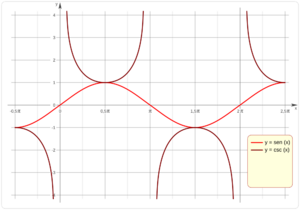
Si observas las gráficas de la función seno (la onda suave) y la función cosecante (las curvas separadas), notarás algo importante.
¿Qué pasa cuando el Seno es cero?
Cuando el valor del seno de un ángulo es cero, la cosecante de ese ángulo se vuelve muy, muy grande (o muy, muy pequeña en el lado negativo). Esto se debe a que no podemos dividir entre cero en matemáticas.
Por ejemplo, si el seno se acerca a cero desde números negativos, la cosecante se va hacia el "infinito negativo":
Y si el seno se acerca a cero desde números positivos, la cosecante se va hacia el "infinito positivo":
Cuando el seno de un ángulo es 1, su cosecante también es 1. Esto se puede ver claramente en la gráfica donde las dos funciones se tocan.
Galería de imágenes
-
Un triángulo básico para entender la trigonometría.
Véase también
En inglés: Trigonometric function Facts for Kids
- Trigonometría
- Identidad trigonométrica
