Producto vectorial para niños
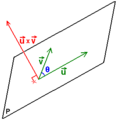
El producto vectorial o producto cruz es una operación matemática especial que se usa con dos vectores en un espacio de tres dimensiones. Imagina que tienes dos flechas (vectores) que salen de un mismo punto. Cuando haces el producto vectorial con ellas, el resultado es una tercera flecha.
Esta nueva flecha tiene algunas características interesantes:
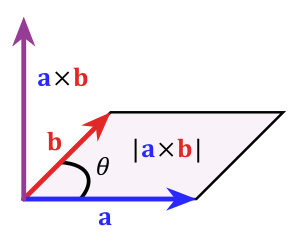
- Es perpendicular (forma un ángulo de 90 grados) a las dos flechas originales. Piensa en una mesa: si una flecha va a lo largo y otra a lo ancho, la tercera flecha apuntaría hacia arriba o hacia abajo, perpendicular a la superficie de la mesa.
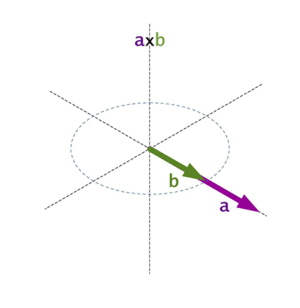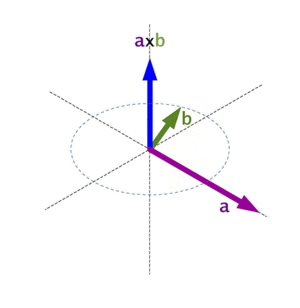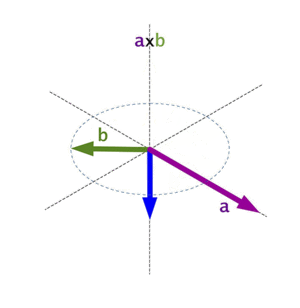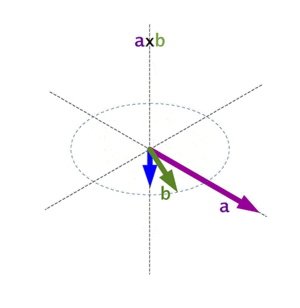
- Su longitud (o magnitud) depende de las longitudes de las flechas originales y del ángulo entre ellas.
- Su dirección se determina usando una regla llamada la "regla de la mano derecha" o "regla del sacacorchos".
El producto vectorial es muy útil para resolver problemas en Física y ingeniería, especialmente cuando se necesita encontrar una dirección que sea perpendicular a otras dos, como en el cálculo de fuerzas o movimientos.
Contenido
¿Cómo se define el producto vectorial?
Para entender el producto vectorial, imaginemos dos vectores, a los que llamaremos a y b. Ambos están en un espacio de tres dimensiones. El producto vectorial de a y b se escribe como a × b (por eso se le llama "producto cruz"). El resultado es un nuevo vector, al que llamaremos c.
La longitud del vector resultante c se calcula así:
Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ||\mathbf{a}|| \cdot ||\mathbf{b}|| \cdot \sen{\theta}
Donde:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ||\mathbf{a}|| es la longitud del vector a.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ||\mathbf{b}|| es la longitud del vector b.
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \sen{\theta} es el seno del ángulo más pequeño (
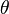) entre los vectores a y b.
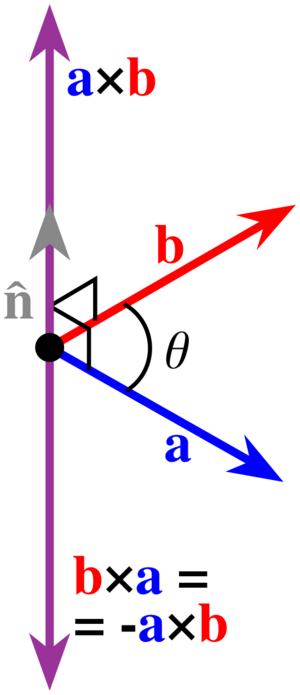
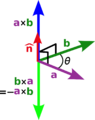
La dirección del vector c es perpendicular a los vectores a y b. Para saber si apunta "hacia arriba" o "hacia abajo" (o en qué sentido), usamos la regla de la mano derecha.
La regla de la mano derecha
Imagina que pones tu mano derecha de forma que tus dedos apunten en la dirección del primer vector (a). Luego, doblas tus dedos hacia la dirección del segundo vector (b) por el camino más corto. La dirección en la que apunta tu pulgar extendido es la dirección del vector resultante (c). Es como girar un sacacorchos: si giras de a hacia b, el sacacorchos avanza en la dirección de c.
Calculando el producto vectorial con componentes
Los vectores en un espacio de tres dimensiones se pueden escribir con tres números, que son sus "componentes" en los ejes x, y, z. Por ejemplo, un vector u puede ser Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (u_x, u_y, u_z) .
Si tenemos dos vectores, u = Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (u_x, u_y, u_z) y v = Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (v_x, v_y, v_z) , el vector resultante w = u × v tiene las siguientes componentes:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): w_x = u_y v_z - u_z v_y
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): w_y = u_z v_x - u_x v_z
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): w_z = u_x v_y - u_y v_x
Estas fórmulas pueden parecer complicadas, pero son la forma precisa de calcular el producto vectorial cuando conoces las componentes de los vectores.
Ejemplo de cálculo
Vamos a calcular el producto vectorial de dos vectores:
- a = (2, 0, 1)
- b = (1, -1, 3)
Usando las fórmulas de las componentes:
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c_x = (0)(3) - (1)(-1) = 0 - (-1) = 1
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c_y = (1)(1) - (2)(3) = 1 - 6 = -5
- Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): c_z = (2)(-1) - (0)(1) = -2 - 0 = -2
Así, el vector resultante c es (1, -5, -2).
Para comprobar que este vector es perpendicular a los originales, se puede usar el Producto escalar. Si el producto escalar de c con a (o con b) es cero, significa que son perpendiculares.
Propiedades importantes del producto vectorial
El producto vectorial tiene algunas propiedades que lo hacen único:
- No es asociativo: Esto significa que el orden en que agrupas las operaciones importa. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): (\mathbf a \times \mathbf b)\times \mathbf c no es lo mismo que Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf a \times (\mathbf b \times \mathbf c) .
- Es anticonmutativo: Si cambias el orden de los vectores, el resultado es el mismo vector pero en la dirección opuesta. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf a \times \mathbf b = - (\mathbf b \times \mathbf a) .
- Perpendicularidad: El producto vectorial de a y b siempre es perpendicular a a y a b. Por lo tanto, el producto escalar de Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf a \cdot ( \mathbf a \times \mathbf b ) siempre es cero.
- Paralelismo: Si el producto vectorial de dos vectores es el vector cero (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbf 0 ), significa que los vectores son paralelos entre sí.
- Distributividad: Se puede "distribuir" sobre la suma de vectores:
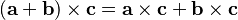. - Área de un paralelogramo: La longitud del producto vectorial Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): ||\mathbf a \times \mathbf b|| es igual al área del paralelogramo que forman los vectores a y b cuando se dibujan desde el mismo punto.
Volumen de un paralelepípedo
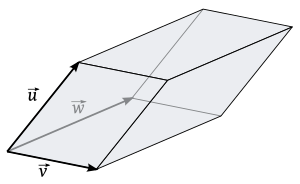
El producto vectorial también nos ayuda a calcular el volumen de un paralelepípedo (una figura con seis caras que son paralelogramos, como una caja inclinada).
Si tienes tres vectores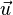 
, 
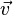y 
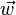que forman los lados de un paralelepípedo, el volumen se puede calcular con una operación llamada "triple producto escalar". Esta operación combina el producto vectorial y el producto escalar: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): V = |\vec{w}\cdot(\vec{u}\times\vec{v})| Esto significa que primero calculas el producto vectorial de dos vectores (por ejemplo, 
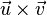), lo que te da un vector perpendicular a la base. Luego, haces el producto escalar de ese resultado con el tercer vector (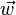). El valor absoluto de este resultado es el volumen del paralelepípedo.
Otros tipos de productos entre vectores
Además del producto vectorial, existen otras operaciones de "producto" entre vectores:
- Producto escalar: El resultado es un número (un escalar), no un vector. Se usa para calcular ángulos y longitudes.
- Producto tensorial: Es una operación más avanzada que se usa en matemáticas y física para combinar vectores de una manera diferente.
El producto vectorial es una herramienta fundamental en matemáticas y ciencias, que nos permite entender y describir relaciones espaciales y fenómenos físicos en tres dimensiones.
Galería de imágenes
-
Relaciones entre los vectores.
-
Producto vectorial.
Véase también
En inglés: Cross product Facts for Kids
