Logaritmo para niños
Datos para niños Logaritmo |
||
|---|---|---|
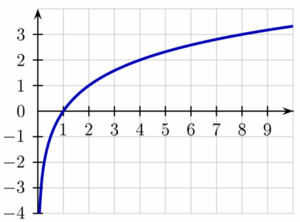
 Gráfica de Logaritmo
|
||
| Definición | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b(x) := \frac {\ln(x)}{\ln(b)} Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b\in\mathbb{R}^+-\{1\} |
|
| Tipo | Función real | |
| Descubridor(es) | John Napier (1614) | |
| Dominio | Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \mathbb{R}^{+} | |
| Codominio | 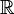 |
|
| Imagen |  |
|
| Propiedades | Biyectiva Cóncava Estrictamente creciente Trascendente |
|
| Cálculo infinitesimal | ||
| Derivada | 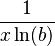 |
|
| Función inversa | 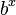 o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{x\cdot\ln(b)} o Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): e^{x\cdot\ln(b)} |
|
| Límites | 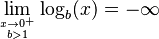  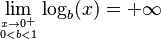 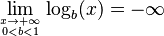 |
|
| Funciones relacionadas | Función exponencial | |
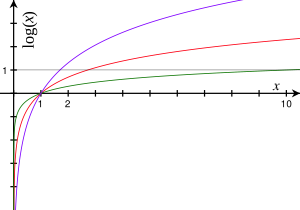
| El rojo representa el logaritmo en base e. El verde corresponde a la base 10. El púrpura al de la base 1,7. |
||
En matemáticas, un logaritmo es una forma de encontrar el exponente de un número. Imagina que tienes una base (un número) y quieres saber a qué potencia debes elevarla para obtener otro número. Esa potencia es el logaritmo.
Se escribe así: Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_{b}n=x . Esto significa que si elevas la base b a la potencia x, obtendrás el número n. Es decir, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^x=n .
Por ejemplo, el logaritmo de 1000 en base 10 es 3. Esto es porque 10 elevado a la potencia 3 (10 x 10 x 10) es igual a 1000. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_{10}1000 = 3 \quad \Leftrightarrow\ \quad 10^3 = 1000
La base de un logaritmo siempre debe ser un número positivo y diferente de 1.
Contenido
Logaritmo: ¿Qué es y para qué sirve?
El logaritmo es una operación matemática que es lo contrario de la potenciación. Así como la resta es lo opuesto a la suma, y la división es lo opuesto a la multiplicación, el logaritmo es lo opuesto a elevar un número a una potencia.
Para escribir un logaritmo, usamos la abreviatura "log". La base se escribe como un número pequeño debajo de "log", y luego el número del que queremos hallar el logaritmo. Por ejemplo, si 3 elevado a 5 es 243 (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 3^5=243 ), entonces el logaritmo en base 3 de 243 es 5 (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_3 243=5 ). A veces, si la base es muy común, se puede omitir.
¿Quién inventó los logaritmos?
Los logaritmos fueron creados por John Napier en 1614. Él los inventó para hacer los cálculos más sencillos. En esa época, no existían las calculadoras ni los ordenadores. Los científicos, ingenieros y banqueros los usaban con reglas de cálculo y tablas especiales para hacer operaciones grandes de forma rápida.
Leonhard Euler en el siglo XVIII conectó los logaritmos con la función exponencial y usó la letra e para la base de los logaritmos naturales.
Cómo entender los logaritmos
Los logaritmos son muy útiles porque pueden transformar operaciones complicadas en otras más sencillas:
- Una multiplicación se convierte en una suma.
- Una división se convierte en una resta.
- Una potencia se convierte en una multiplicación.
- Una raíz se convierte en una división.
Hoy en día, con las calculadoras y los ordenadores, los logaritmos siguen siendo importantes en muchas áreas.
Definición detallada del logaritmo
El logaritmo de un número x en una base b es el exponente n al que se debe elevar b para obtener x. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b(x)=n\Leftrightarrow b^n=x
Se lee: "logaritmo en base b de x es igual a n, si y solo si b elevado a n da como resultado x."
Para que esto funcione, la base b debe ser un número positivo y diferente de 1. El número x (al que le calculamos el logaritmo) también debe ser positivo.
Por ejemplo, en la expresión Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): 10^2 =100 , el logaritmo en base 10 de 100 es 2. Se escribe Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_{10}(100)=2 .
Propiedades básicas de los logaritmos
Los logaritmos tienen algunas propiedades que siempre se cumplen, sin importar la base:
- El logaritmo de su propia base siempre es 1. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b b = 1 , porque Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): b^1 = b .
- El logaritmo de 1 siempre es 0. Por ejemplo, Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b 1 = 0 , porque
 .
.
Los números negativos no tienen logaritmo en el conjunto de los números reales. Esto es porque cualquier número positivo elevado a cualquier potencia siempre dará un resultado positivo.
Las potencias de una base forman una progresión geométrica (multiplicando siempre por el mismo número), y sus exponentes forman una progresión aritmética (sumando siempre el mismo número). Por ejemplo, las potencias de 2 son 1, 2, 4, 8, 16... (multiplicando por 2 cada vez). Sus logaritmos en base 2 son 0, 1, 2, 3, 4... (sumando 1 cada vez).
Propiedades para simplificar cálculos
Los logaritmos tienen propiedades muy útiles para simplificar operaciones:
- El logaritmo de una multiplicación es la suma de los logaritmos:
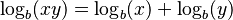
- El logaritmo de una división es la resta de los logaritmos:
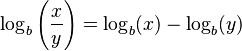
- El logaritmo de una potencia es el exponente multiplicado por el logaritmo de la base:
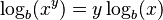
- El logaritmo de una raíz es el logaritmo del número dividido por el índice de la raíz:
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](/images/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
Tipos de logaritmos y cambio de base
Hay varios tipos de logaritmos que se usan mucho:
- El logaritmo natural, que usa la base e (un número especial en matemáticas, aproximadamente 2.71828). Se escribe como
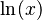 .
. - El logaritmo decimal, que usa la base 10. Se escribe como
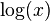 .
. - El logaritmo binario, que usa la base 2.
Puedes cambiar la base de un logaritmo usando esta fórmula: 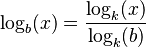 Donde k puede ser cualquier base válida.
Donde k puede ser cualquier base válida.
El logaritmo natural es muy importante en física, matemáticas e ingeniería. El logaritmo decimal se usa en ciencias para medir cosas como la acidez (pH), la intensidad de sonido (dB) o la energía de un terremoto (escala sismológica de Richter). En informática, el logaritmo en base 2 es muy común.
La función logarítmica y su inversa
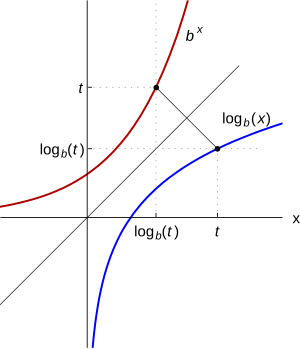
La función logarítmica es la función inversa de la función exponencial. Esto significa que si aplicas una función y luego su inversa, vuelves al número original.
Por ejemplo, si elevas un número b a la potencia x (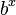 ) y luego calculas el logaritmo en base b de ese resultado, obtendrás x de nuevo. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b (b^x) = x
) y luego calculas el logaritmo en base b de ese resultado, obtendrás x de nuevo. Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b (b^x) = x
De la misma manera, si calculas el logaritmo en base b de un número y (Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b(y) ) y luego elevas b a ese resultado, obtendrás y de nuevo. 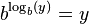
Los gráficos de una función y su inversa son como un espejo. Si dibujas una línea diagonal (donde x es igual a y), verás que los gráficos se reflejan uno al otro.
Cómo crece o decrece la función logarítmica
Si la base b es mayor que 1, la función logarítmica Error al representar (Falta el ejecutable <code>texvc</code>. Véase math/README para configurarlo.): \log_b(x) siempre crece. Esto significa que a medida que x se hace más grande, el valor del logaritmo también se hace más grande.
Si la base b está entre 0 y 1, la función logarítmica decrece. Esto significa que a medida que x se hace más grande, el valor del logaritmo se hace más pequeño.
En cualquier caso, el gráfico de la función logarítmica siempre cruza el eje horizontal en el punto (1,0).
Historia de los logaritmos

El método de los logaritmos fue presentado por primera vez por John Napier en 1614 en su libro Mirifici Logarithmorum Canonis Descriptio. Otro matemático, Joost Bürgi, también los descubrió, pero publicó su trabajo cuatro años después que Napier.
Este método fue muy importante para el avance de la ciencia, especialmente en la astronomía, porque facilitaba cálculos muy difíciles. Antes de que existieran las calculadoras y los ordenadores, los logaritmos se usaban mucho en geodesia (medición de la Tierra), navegación marítima y otras áreas de las matemáticas aplicadas.
Napier llamó a los logaritmos "números artificiales" al principio. La palabra "logaritmo" viene de dos palabras griegas: logos (proporción) y arithmos (número). Significa "un número que indica una relación o proporción". Esto se refiere a que la diferencia entre dos logaritmos muestra la relación entre los números originales.
Galería de imágenes
Véase también
 En inglés: Logarithm Facts for Kids
En inglés: Logarithm Facts for Kids