Codominio para niños
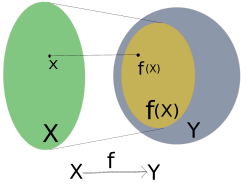
En matemáticas, el codominio (también llamado conjunto de llegada o conjunto final) de una función es un grupo de valores al que pertenecen todos los posibles resultados de esa función. Imagina que es como una caja grande donde la función puede dejar sus respuestas.
El codominio es diferente de la imagen de una función. La imagen es el grupo de valores que la función realmente produce. El codominio, en cambio, puede contener otros valores que la función no llega a producir. Si la imagen y el codominio son exactamente iguales, decimos que la función es una función sobreyectiva.
Por ejemplo, si tenemos una función que "multiplica por 2" los números naturales (1, 2, 3, ...), el codominio podrían ser todos los números naturales. Sin embargo, la imagen de esta función serían solo los números pares (2, 4, 6, ...), porque ningún número impar puede ser el doble de un número natural.
Contenido
¿Qué es el Codominio?
Cuando usamos una función en matemáticas, esta toma un valor de entrada y nos da un valor de salida. El codominio es el conjunto de todos los valores que la función podría producir como resultado. Es como el "universo" de posibles respuestas.
Codominio vs. Imagen (o Rango)
Es muy importante entender la diferencia entre el codominio y la imagen (también conocida como rango).
- El codominio es el conjunto más grande de valores donde la función podría terminar.
- La imagen es el conjunto de todos los valores que la función realmente produce.
Piensa en ello así: si una función es como un arquero, el codominio es todo el campo donde las flechas podrían caer. La imagen, en cambio, son solo los lugares donde las flechas realmente cayeron. La imagen siempre es parte del codominio.
Ejemplos Sencillos para Entenderlo
Ejemplo 1: Multiplicar por 2
Imagina una función que toma un número natural (como 1, 2, 3, etc.) y lo multiplica por 2.
- Si el número de entrada es 1, el resultado es 2.
- Si el número de entrada es 2, el resultado es 4.
- Si el número de entrada es 3, el resultado es 6.
En este caso, el codominio podría ser el conjunto de todos los números naturales. Pero la imagen de esta función serían solo los números pares (2, 4, 6, ...), porque nunca obtendremos un número impar al multiplicar un número natural por 2.
Ejemplo 2: Números al Cuadrado
Considera una función que toma cualquier número real (positivos, negativos, cero, decimales) y lo eleva al cuadrado (lo multiplica por sí mismo). Por ejemplo, si la función es f(x) = x².
- Si x es 2, f(x) es 4.
- Si x es -3, f(x) es 9.
- Si x es 0, f(x) es 0.
El codominio de esta función podría ser el conjunto de todos los números reales. Sin embargo, cuando elevas un número al cuadrado, el resultado siempre es positivo o cero. Por lo tanto, la imagen de esta función es el conjunto de todos los números reales positivos, incluyendo el cero (como 0, 1, 4, 9, etc.).
Conceptos Relacionados
Dominio de una Función
El dominio de una función es el conjunto de todos los valores de entrada que la función puede aceptar. Es decir, son los números o elementos con los que la función puede trabajar.
Imagen de una Función
La imagen (o rango) de una función es el conjunto de todos los valores de salida que la función realmente produce. Como vimos, la imagen es siempre un subconjunto del codominio.
Véase también
 En inglés: Range (mathematics) Facts for Kids
En inglés: Range (mathematics) Facts for Kids